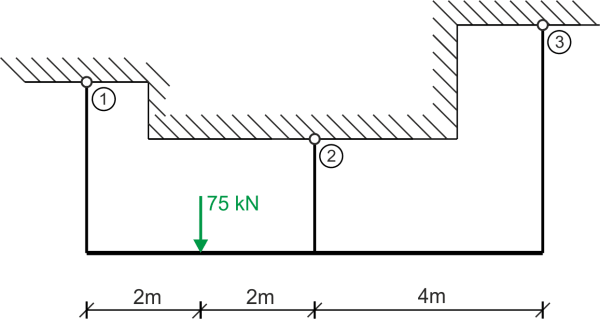
Rozwiązanie YT

Wersja klasyczna

Suma rzutów sił na oś x nic nam nie daje, więc mamy dwa efektywne równania równowagi statycznej. Niewiadome są siły w trzech prętach, a więc zadanie jest jednokrotnie statycznie niewyznaczalne, do jego rozwiązanie musimy wykorzystać dodatkowy warunek - geometryczny (z planu przemieszczeń).
Równania równowagi:
\begin{aligned} &\sum{M_{C}}=0\\ &N_{1}\cdot 4 - 75\cdot 2 - N_{3}\cdot 4 = 0\\ &N_{1}=\frac{150 + 4\cdot N_{3}}{4}\\ &N_{1}=37,5 + N_{3}\\ &\sum{Y}=0\\ &N_{1} - 75 + N_{2} + N_{3} =0\\ &37,5 + N_{3} - 75 + N_{3}=-N_{2}\\ &N_{2}=37,5 - 2N_{3} \end{aligned}
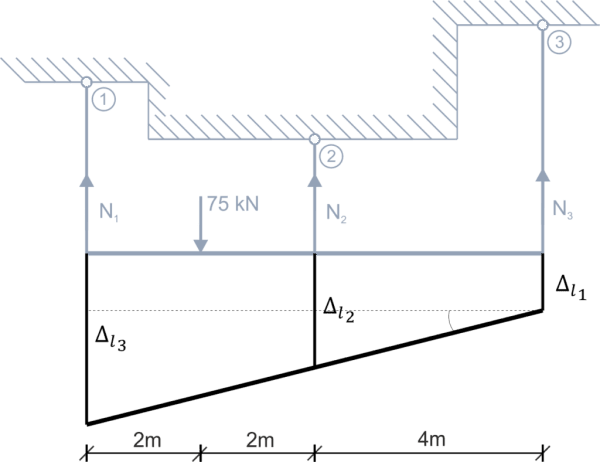
Warunek geometryczny \begin{aligned} &\frac{\Delta l_{3}-\Delta l_{1}}{8}=\frac{\Delta l_{2}-\Delta l_{1}}{4}\\ \end{aligned} Przekształcam i rozwiązuję warunek geometryczny \begin{aligned} &\Delta l_{3}-\Delta l_{1}=2(\Delta l_{2}-\Delta l_{1})\\ &\Delta l_{3}+\Delta l_{1}-2\cdot \Delta l_{2}=0\\ &\Delta l=\frac{N\cdot l}{E\cdot A}\\ &\frac{N_{3}\cdot 4}{E_{3}\cdot A_{3}}+\frac{N_{1}\cdot 3}{E_{1}\cdot A_{1}}-2\cdot \frac{N_{2}\cdot 2}{E_{2}\cdot A_{2}}=0 \end{aligned} Z treści zadania: \begin{aligned} &A_{1}=A_{2}=2A_{3}\\ &\frac{E_{2}}{E_{1}}=\frac{105 \ GPa}{210 \ GPa}=\frac{1}{2} & \Rightarrow 2E_{2}=E_{1}\\ &E_{1}=E_{3}\\ \end{aligned} Podstawiam te zależności do wcześniejszego równania \begin{aligned} &\frac{N_{3}\cdot 4}{2E_{2}\cdot A_{3}}+\frac{(37,5 + N_{3})\cdot 3}{2E_{2}\cdot 2A_{3}} - 2\cdot\frac{(37,5 - 2N_{3})\cdot 2}{E_{2}\cdot 2A_{3}}=0 & |\cdot E_{2}A_{3}\\ &2N_{3} + \frac{3}{4}(37,5 + N_{3}) - 2(37,5 - 2M_{3})=0\\ &2N_{3} + 28,125 + 0,75N_{3} - 75 + 2N_{3}\\ &4,75N_{3}=46,875\\ &N_{3}=9,868 \ kN \end{aligned} Wracam do zależności z równań równowagi statycznej i obliczam siły w pozostałych prętach \begin{aligned} &N_{1}=37,5 + N_{3}=47,368 \ kN\\ &N_{2}=37,5 - 2N_{3}=17,764 \ kN\\ \end{aligned} Rozwiązuję warunek wytrzymałości dla wszystkich prętów \begin{aligned} &\sigma=\frac{N}{A}\\ &\sigma_{1}=\frac{47,368\cdot 10^{3}}{A_{1}}\le 120\cdot 10^{6} & \Rightarrow & A_{1}\ge 3,95\cdot 10^{-4} \ m^{2}\\ &\sigma_{2}=\frac{17,764\cdot 10^{3}}{A_{2}}\le 30\cdot 10^{6} & \Rightarrow & A_{2}\ge 5,92\cdot 10^{-4} \ m^{2}\\ &\sigma_{3}=\frac{9,868\cdot 10^{3}}{A_{3}}\le 120\cdot 10^{6} & \Rightarrow & A_{3}\ge 8,22\cdot 10^{-5} \ m^{2}\\ \end{aligned} Przyjmuję ostatecznie pole przekroju dla prętów pamiętając o zależności z treści zadania \begin{aligned} &A_{1}=A_{2}=2A_{3}\\ &A_{1}=A_{2}=6\cdot 10^{-4}\\ &A_{3}=\frac{1}{2}\cdot 6\cdot 10^{-4}=3\cdot 10^{-4}\\ \end{aligned} Obliczam naprężenia w prętach dla przyjętego pola przekroju poprzecznego \begin{aligned} &\sigma_{1}=\frac{47,368\cdot 10^{3}}{6\cdot 10^{-4}}=78,95 \ MPa\\ &\sigma_{2}=\frac{17,764\cdot 10^{3}}{6\cdot 10^{-4}}=29,60 \ MPa\\ &\sigma_{3}=\frac{9,868\cdot 10^{3}}{3\cdot 10^{-4}}=32,89 \ MPa\\ \end{aligned}