Solution
Classic version
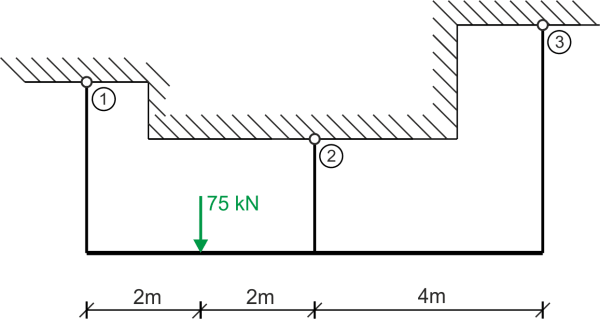
The sum of the forces in the x-axis doesn't give us any information, so we have two effective equilibrium equations. The unknowns are the forces in three rods, so the problem is statically indeterminate once, and to solve it we need to use an additional geometric condition (from the displacement plan). Equilibrium equations:\begin{aligned} &\sum{M_{C}}=0\\ &N_{1}\cdot 4 - 75\cdot 2 - N_{3}\cdot 4 = 0\\ &N_{1}=\frac{150 + 4\cdot N_{3}}{4}\\ &N_{1}=37.5 + N_{3}\\ &\sum{Y}=0\\ &N_{1} - 75 + N_{2} + N_{3} =0\\ &37.5 + N_{3} - 75 + N_{3}=-N_{2}\\ &N_{2}=37.5 - 2N_{3} \end{aligned}
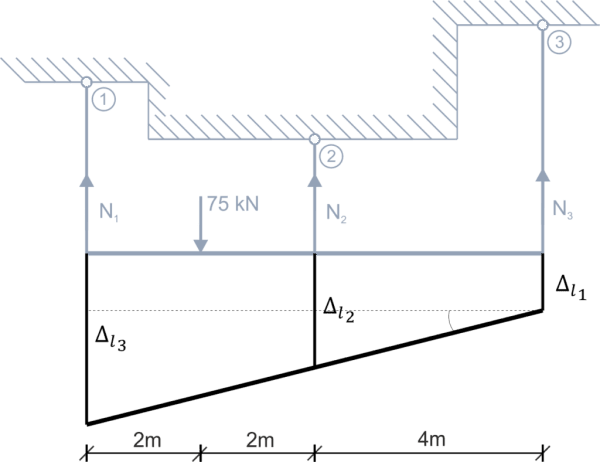
Geometric condition \begin{aligned} &\frac{\Delta l_{3}-\Delta l_{1}}{8}=\frac{\Delta l_{2}-\Delta l_{1}}{4}\\ \end{aligned} Transform and solve the geometric condition \begin{aligned} &\Delta l_{3}-\Delta l_{1}=2(\Delta l_{2}-\Delta l_{1})\\ &\Delta l_{3}+\Delta l_{1}-2\cdot \Delta l_{2}=0\\ &\Delta l=\frac{N\cdot l}{E\cdot A}\\ &\frac{N_{3}\cdot 4}{E_{3}\cdot A_{3}}+\frac{N_{1}\cdot 3}{E_{1}\cdot A_{1}}-2\cdot \frac{N_{2}\cdot 2}{E_{2}\cdot A_{2}}=0 \end{aligned} From the problem statement: \begin{aligned} &A_{1}=A_{2}=2A_{3}\\ &\frac{E_{2}}{E_{1}}=\frac{105 \ GPa}{210 \ GPa}=\frac{1}{2} & \Rightarrow 2E_{2}=E_{1}\\ &E_{1}=E_{3}\\ \end{aligned} Substitute these relationships into the previous equation \begin{aligned} &\frac{N_{3}\cdot 4}{2E_{2}\cdot A_{3}}+\frac{(37.5 + N_{3})\cdot 3}{2E_{2}\cdot 2A_{3}} - 2\cdot\frac{(37.5 - 2N_{3})\cdot 2}{E_{2}\cdot 2A_{3}}=0 & |\cdot E_{2}A_{3}\\ &2N_{3} + \frac{3}{4}(37.5 + N_{3}) - 2(37.5 - 2M_{3})=0\\ &2N_{3} + 28.125 + 0.75N_{3} - 75 + 2N_{3}\\ &4.75N_{3}=46.875\\ &N_{3}=9.868 \ kN \end{aligned} Go back to the relationships from the static equilibrium equations and calculate the forces in the remaining rods \begin{aligned} &N_{1}=37.5 + N_{3}=47.368 \ kN\\ &N_{2}=37.5 - 2N_{3}=17.764 \ kN\\ \end{aligned} Solve the strength condition for all rods \begin{aligned} &\sigma=\frac{N}{A}\\ &\sigma_{1}=\frac{47.368\cdot 10^{3}}{A_{1}}\le 120\cdot 10^{6} & \Rightarrow & A_{1}\ge 3.95\cdot 10^{-4} \ m^{2}\\ &\sigma_{2}=\frac{17.764\cdot 10^{3}}{A_{2}}\le 30\cdot 10^{6} & \Rightarrow & A_{2}\ge 5.92\cdot 10^{-4} \ m^{2}\\ &\sigma_{3}=\frac{9.868\cdot 10^{3}}{A_{3}}\le 120\cdot 10^{6} & \Rightarrow & A_{3}\ge 8.22\cdot 10^{-5} \ m^{2}\\ \end{aligned} Finally, assume the cross-sectional area for the rods, keeping in mind the relationship from the problem statement \begin{aligned} &A_{1}=A_{2}=2A_{3}\\ &A_{1}=A_{2}=6\cdot 10^{-4}\\ &A_{3}=\frac{1}{2}\cdot 6\cdot 10^{-4}=3\cdot 10^{-4}\\ \end{aligned} Calculate the stresses in the rods for the assumed cross-sectional area \begin{aligned} &\sigma_{1}=\frac{47.368\cdot 10^{3}}{6\cdot 10^{-4}}=78.95 \ MPa\\ &\sigma_{2}=\frac{17.764\cdot 10^{3}}{6\cdot 10^{-4}}=29.60 \ MPa\\ &\sigma_{3}=\frac{9.868\cdot 10^{3}}{3\cdot 10^{-4}}=32.89 \ MPa\\ \end{aligned}
If you have any questions, comments, or think you have found a mistake in this solution, please send us a message at kontakt@edupanda.pl.