Rozwiązanie
Dla dociekliwych dodaję link do rozwiązania w Robot Structural Analysis:
kratownica1.rtd
Przykład obliczeniowy z komentarzem
Treść
Dla danej kratownicy wskazać pręty zerowe oraz wyznaczyć siły we wszystkich prętach metodą Rittera.
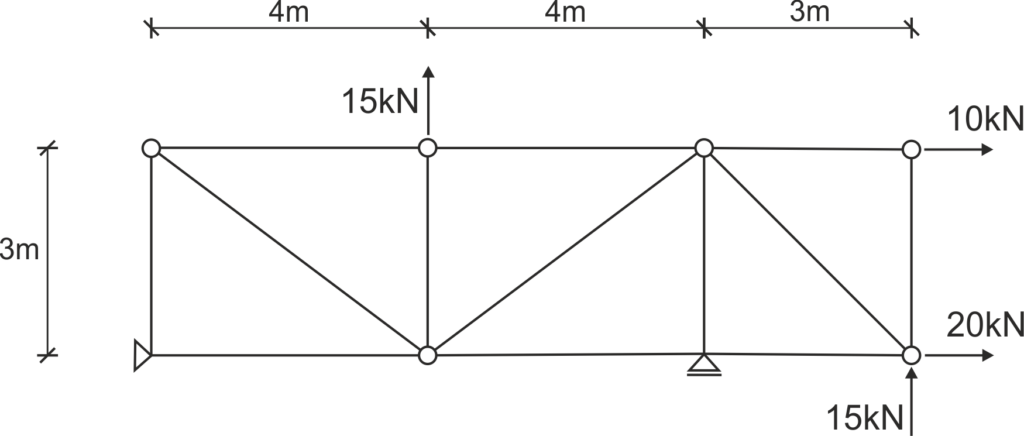
Rozwiązanie
Krok 1
Ponumerowanie prętów, ewentualne oznaczenie węzłów, zaznaczenie reakcji podporowych.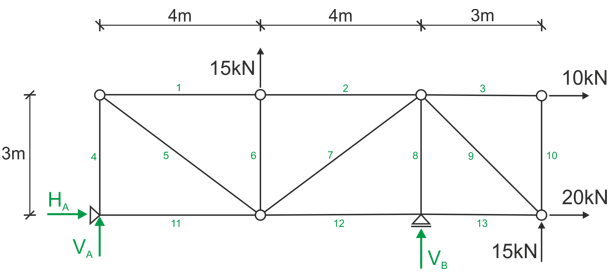
Krok 2
Rozpisanie równań równowagi statycznej i obliczenie reakcji podporowych.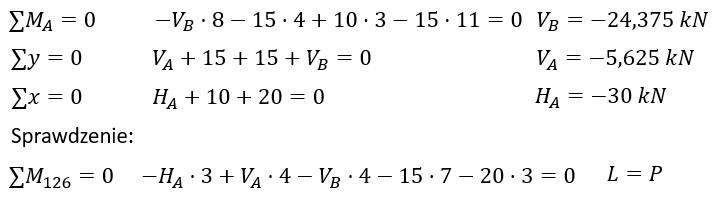
Krok 3
Robimy przecięcia Rittera.Możemy zacząć w zasadzie w dowolny sposób, byleby nie przeciąć przez więcej niż 3 pręty, ponieważ tyle niewiadomych jesteśmy w stanie policzyć w jednym wycięciu.
Rozpocznijmy od przecięcia przez pręty 2,7 oraz 12 i zróbmy widok z lewej strony
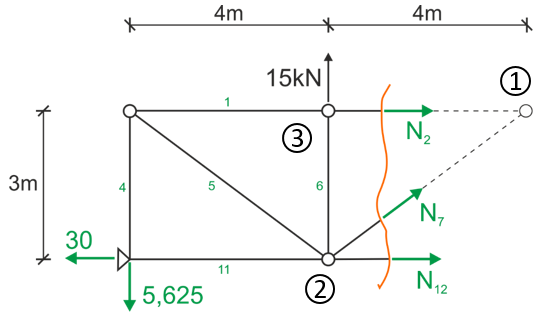
Zapisujemy równania równowagi statycznej.
Tak zwane punkty Rittera są do punkty przecięcia się kierunków dwóch niewiadomych.Na rysunku powyżej siły N2 i N7 przecinają się w punkcie (1) a siły N7 i N12 przecinają się w punkcie (2) - są to właśnie punkty Rittera. Najczęściej zapisujemy sumy momentów w punktach Rittera, zdarza się że takich punktów jest więcej niż dwa, jeśli siły są pod różnymi kątami, wtedy możemy zapisać trzy równania w postaci sumy momentów.
Jeśli natomiast mamy tylko dwa punkty Rittera tak jak tutaj to nie szkodzi, zapisujemy dwie sumy momentów i jako trzecie równanie możemy zapisać albo sumę rzutów na oś "x". albo (lepiej) na "y", bo tylko niewiadoma N7 wchodzi do tego równania.
Możemy też zapisać sumę momentów w innym punkcie, tak żeby policzyć ostatnią niewiadomą, tutaj wyznaczono punkt (3).
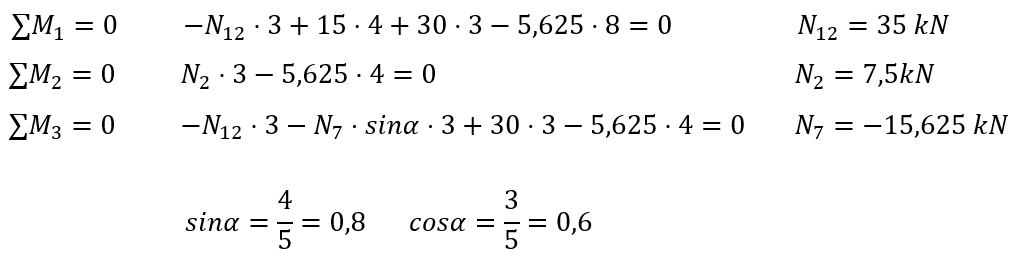
Analogicznie robimy w przecięciu Rittera przez pręty 1,5,11.
Widok z lewej strony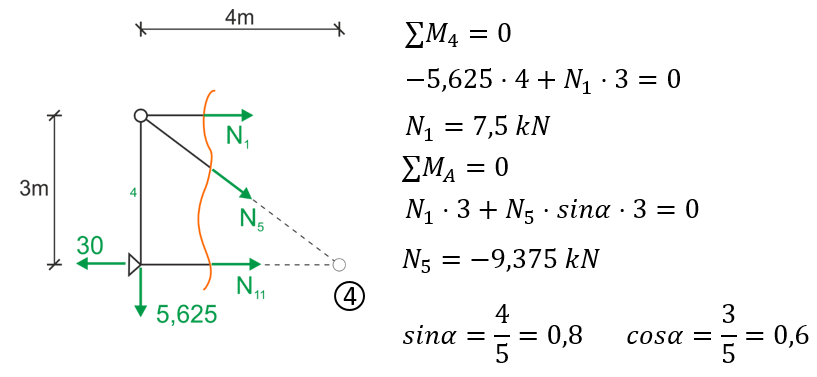
Ostatnie będzie przecięcie Rittera przez pręty 3,9,13.
Widok z prawej strony
Krok 5
Dokończenie rozwiązania zadania.Narysujmy wykres sił normalnych w prętach które już mamy policzone.
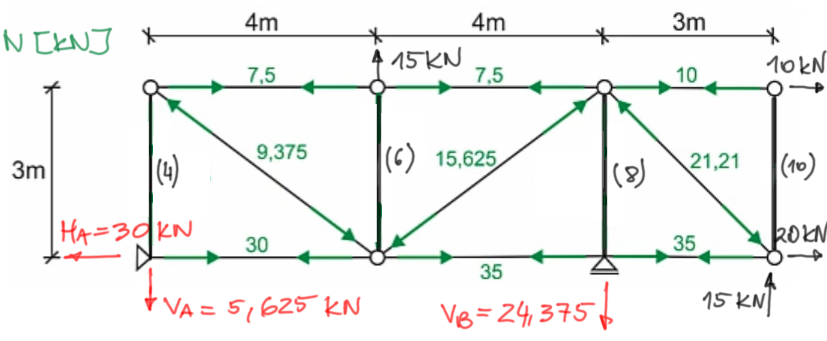
Wykres sił normalnych, znakowanie:
DODATNIE

UJEMNE

Policzyliśmy siły w większej części prętów (9 z 13). Pozostały nam 4 pręty (pionowe 4,6,8 i 10), mamy trzy możliwości:
- robić kolejne wycięcia, tylko już potrzebujemy czterech osobnych przecięć, żeby policzyć te siły, co się trochę mija z celem.
- zrobić równowagę węzłów A,B, (3-10) oraz (1-2-6) i doliczyć ostatnie cztery siły, na pewno mniej rysowania wycinając pojedynczy węzeł niż robiąc większe wycięcie,
- sprytnie zauważyć, że:
1) z drugiego twierdzenia o prętach zerowych pręt (10) jest zerowy,
2) z drugiego twierdzenia w zasadzie wynika
dodatkowa zasada - jeżeli siła obciąża węzeł w taki sposób, że jej kierunek jest współliniowy z jednym z prętów i żadna inna siła nie daje się rzutować na tą prostą, to siła w pręcie przekazuje się współliniowo.
Spójrzmy na pas dolny i węzeł B - siła 35kN w pręcie poziomym przechodzi z pręta na pręt jak widać na wykresie
natomiast reakcja VB=24,375 kN obciąża współliniowo pręt (8) - więc przekazuje bezpośrednie na niego siłę rozciągającą (bo widzimy że reakcja VB tak działa na pręt (8), że go rozciąga).
ostatecznie z tego znamy siłę w pręcie (8)
3) na tej samej zasadzie N6=15 kN
4) na tej samej zasadzie N4=5,625 kN
Krok 5
Rysujemy ostateczny wykres siły normalnych.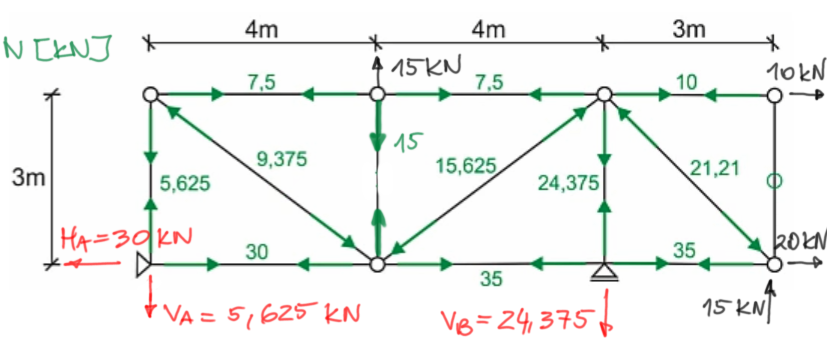
Jeżeli masz jakieś pytania, uwagi lub wydaje Ci się, że znalazłeś błąd w tym rozwiązaniu, napisz proszę do nas wiadomość na kontakt@edupanda.pl lub skontaktuj się z nami przez nasz profil na FB: