Rozwiązanie
Siły przekrojowe
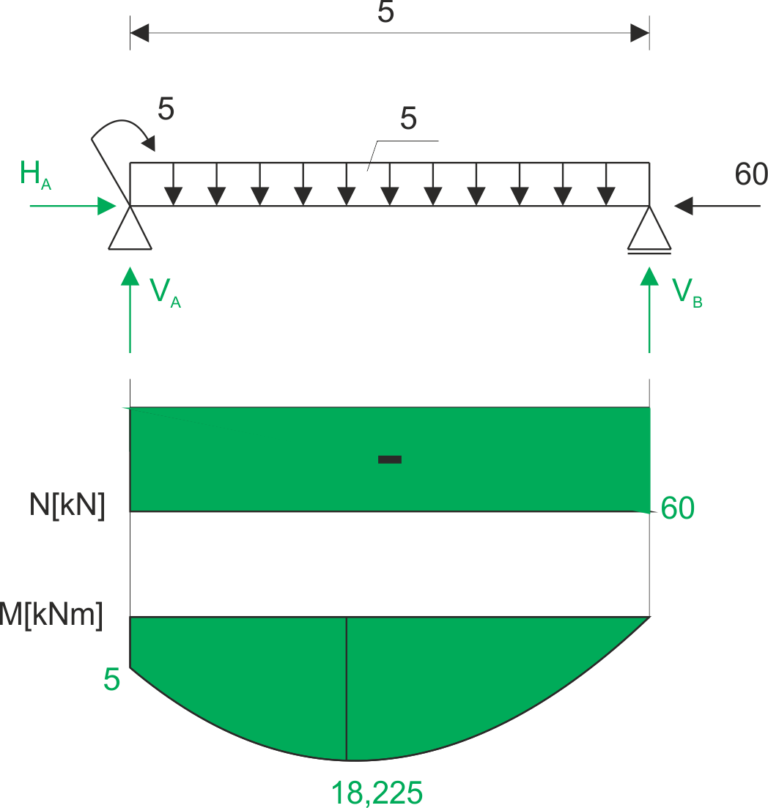
\begin{aligned} &\sum x=0 \\ &H_{A}=60 k N \\ &\sum M_{A}=5+5 \cdot 5 \cdot 2,5-V_{B} \cdot 5=0 \\ &V_{B}=13,5 k N \\ &\sum y=0 \\ &V_{A}-5 \cdot 5+13,5=0 \\ &V_{A}=11,5 k N \end{aligned}Funkcja momentu gnącego:
\begin{aligned} M(x)=5+11,5 x-\frac{1}{2} \cdot 5 \cdot x^{2} \end{aligned}Sprawdzam czy jest ekstremum:
\begin{aligned} &\frac{d M(x)}{d x}=11,5-5 x \\ &11,5-5 x=0 \Rightarrow x=2,3 \\ &M(0)=5 k N m \\ &M(5)=0 k N m \\ &M_{\text {extr }}(2,3)=5+11,5 \cdot 2,3-2,5 \cdot 2,3^{2}=18,225 k N m \end{aligned}Wykres siły normalnej i momentu gnącego
Naprężenia normalne
\begin{aligned} &\sigma_{N}=\frac{N}{A} \\ &A=10 \cdot 50+10 \cdot 70=1200 \mathrm{~cm}^{2} \\ &\sigma_{N}=\frac{-60 \cdot 10^{3}}{1200 \cdot 10^{-4}}=-0,5 \mathrm{MPa} \\ &\sigma_{G}=\frac{M_{y}}{I_{y}} z \end{aligned}Charakterystyki geometryczne
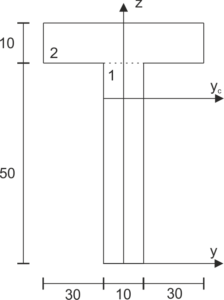 \begin{aligned}
z_{1} &=25 \mathrm{~mm} \\
z_{2} &=55 \mathrm{~mm} \\
A_{1} &=500 \mathrm{~mm}^{2} \\
A_{2} &=700 \mathrm{~mm}^{2} \\
z_{c} &=\frac{z_{1} \cdot A_{1}+z_{2} \cdot A_{2}}{A_{1}+A_{2}}=42,5 \mathrm{~mm} \\
I_{y c} &=\frac{10 \cdot 50^{3}}{12}+500 \cdot(25-42,5)^{2}+\frac{70 \cdot 10^{3}}{12}+700 \cdot(55-42,5)^{2}=372500 \mathrm{~cm}^{4} \\
\sigma_{G}^{d} &=\frac{18,225 \cdot 10^{3}}{372500 \cdot 10^{-8}} \cdot 0,0425=0,21 \mathrm{MPa} \\
\sigma_{G}^{g} &=\frac{18,225 \cdot 10^{3}}{372500 \cdot 10^{-8}} \cdot(0,06-0,0425)=-0,09 \mathrm{MPa}
\end{aligned}
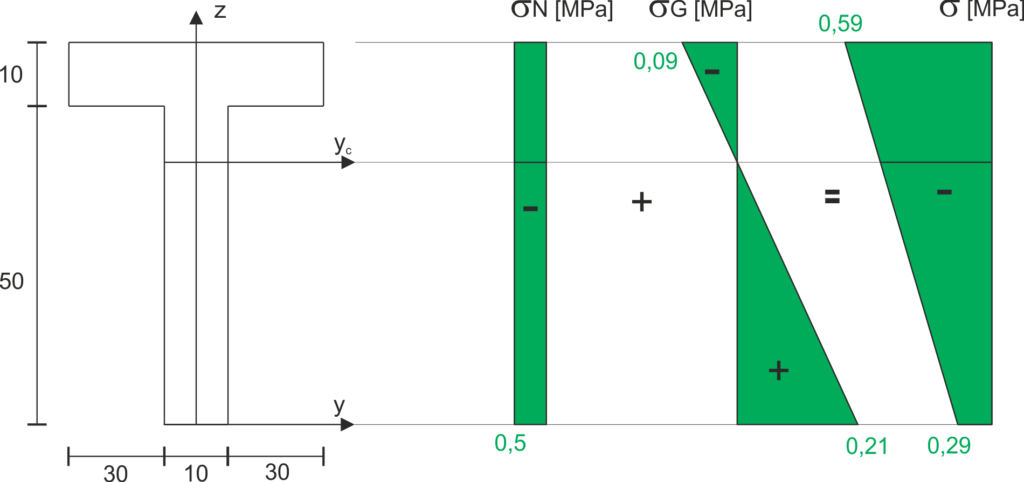
Wykres ostateczny naprężeń normalnych otrzymujemy przez dodanie w punktach
charakterystycznych (na dolnych i górnych włóknach) naprężeń od ściskania i zginania
\begin{aligned}
z_{1} &=25 \mathrm{~mm} \\
z_{2} &=55 \mathrm{~mm} \\
A_{1} &=500 \mathrm{~mm}^{2} \\
A_{2} &=700 \mathrm{~mm}^{2} \\
z_{c} &=\frac{z_{1} \cdot A_{1}+z_{2} \cdot A_{2}}{A_{1}+A_{2}}=42,5 \mathrm{~mm} \\
I_{y c} &=\frac{10 \cdot 50^{3}}{12}+500 \cdot(25-42,5)^{2}+\frac{70 \cdot 10^{3}}{12}+700 \cdot(55-42,5)^{2}=372500 \mathrm{~cm}^{4} \\
\sigma_{G}^{d} &=\frac{18,225 \cdot 10^{3}}{372500 \cdot 10^{-8}} \cdot 0,0425=0,21 \mathrm{MPa} \\
\sigma_{G}^{g} &=\frac{18,225 \cdot 10^{3}}{372500 \cdot 10^{-8}} \cdot(0,06-0,0425)=-0,09 \mathrm{MPa}
\end{aligned}
Wykres ostateczny naprężeń normalnych otrzymujemy przez dodanie w punktach
charakterystycznych (na dolnych i górnych włóknach) naprężeń od ściskania i zginania
Jeżeli masz jakieś pytania, uwagi lub wydaje Ci się, że znalazłeś błąd w tym rozwiązaniu, napisz proszę do nas wiadomość na kontakt@edupanda.pl lub skontaktuj się z nami przez nasz profil na FB:
