Figura nie ma osi symetrii, początkowy układ osi przyjmujemy więc dowolnie.

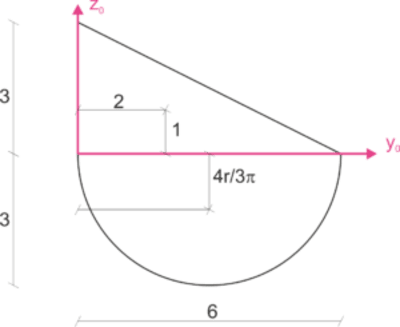
Szukamy dwóch współrzędnych środka ciężkości. Obliczamy je jako iloraz statycznego momentu bezwładności z całkowitym polem przekroju. Dobrze sobie wypisać pomocniczo współrzędne „z-towe” i „y-kowe” środków ciężkości poszczególnych figur prostych (y1, y2 i z1, z2) oraz ich pola (A1 i A2).

Środek ciężkości

\begin{aligned} y_1=2 [cm] & z_1=1 [cm] & A_1=9cm^2\\ y_2=3 [cm] & z_2=-\frac{4r}{3\pi}=-1,273 [cm] & A_2=\frac{\pi r^2}{2}=14,137cm^2\\ \end{aligned} \begin{aligned} &A=A_1+A_2=23,14 [cm^2]\\ &y_c=\frac{2*9+3*14,14}{23,14}=2,611 [cm]\\ &z_c=\frac{1*9-1,273*14,14}{23,14}=-0,389 [cm]\\ \end{aligned}

Zaznaczamy obliczony środek ciężkości na rysunku, osie przeniesione do środka ciężkości to osie centralne. Obliczamy centralne momenty bezwładności.

\begin{aligned} &I_{yc}=\frac{6*3^3}{36}+9*(1-(-0,389))^2+[\frac{\pi r^4}{8}-\frac{8r^4}{9\pi}]+14,137*(-1,273-(-0,389))^2=41,808 [cm^4]\\ &I_{zc}=\frac{6^3*3}{36}+9*(2-2,611)^2+\frac{\pi r^4}{8}+14,137*(3-2,611)^2=55,308 [cm^4]\\ \end{aligned}