Solution
Cross-sectional forces
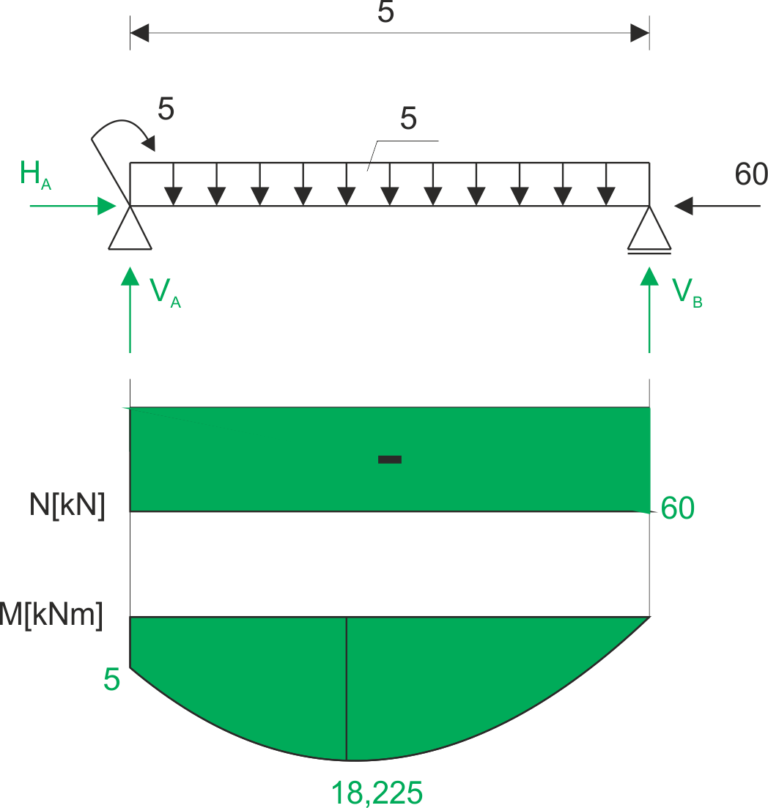
\begin{aligned} &\sum x=0 \\ &H_{A}=60 k N \\ &\sum M_{A}=5+5 \cdot 5 \cdot 2.5-V_{B} \cdot 5=0 \\ &V_{B}=13.5 k N \\ &\sum y=0 \\ &V_{A}-5 \cdot 5+13.5=0 \\ &V_{A}=11.5 k N \end{aligned}Bending moment function:
\begin{aligned} M(x)=5+11.5 x-\frac{1}{2} \cdot 5 \cdot x^{2} \end{aligned}Checking for extremum:
\begin{aligned} &\frac{d M(x)}{d x}=11.5-5 x \\ &11.5-5 x=0 \Rightarrow x=2.3 \\ &M(0)=5 k N m \\ &M(5)=0 k N m \\ &M_{\text {extr }}(2.3)=5+11.5 \cdot 2.3-2.5 \cdot 2.3^{2}=18.225 k N m \end{aligned}Normal force and bending moment graph
Normal stresses
\begin{aligned} &\sigma_{N}=\frac{N}{A} \\ &A=10 \cdot 50+10 \cdot 70=1200 \mathrm{~cm}^{2} \\ &\sigma_{N}=\frac{-60 \cdot 10^{3}}{1200 \cdot 10^{-4}}=-0.5 \mathrm{MPa} \\ &\sigma_{G}=\frac{M_{y}}{I_{y}} z \end{aligned}Geometric characteristics
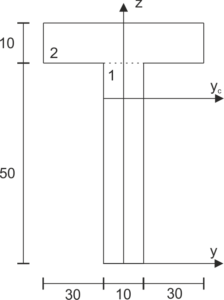 \begin{aligned}
z_{1} &=25 \mathrm{~mm} \\
z_{2} &=55 \mathrm{~mm} \\
A_{1} &=500 \mathrm{~mm}^{2} \\
A_{2} &=700 \mathrm{~mm}^{2} \\
z_{c} &=\frac{z_{1} \cdot A_{1}+z_{2} \cdot A_{2}}{A_{1}+A_{2}}=42.5 \mathrm{~mm} \\
I_{y c} &=\frac{10 \cdot 50^{3}}{12}+500 \cdot(25-42.5)^{2}+\frac{70 \cdot 10^{3}}{12}+700 \cdot(55-42.5)^{2}=372500 \mathrm{~cm}^{4} \\
\sigma_{G}^{d} &=\frac{18.225 \cdot 10^{3}}{372500 \cdot 10^{-8}} \cdot 0.0425=0.21 \mathrm{MPa} \\
\sigma_{G}^{g} &=\frac{18.225 \cdot 10^{3}}{372500 \cdot 10^{-8}} \cdot(0.06-0.0425)=-0.09 \mathrm{MPa}
\end{aligned}
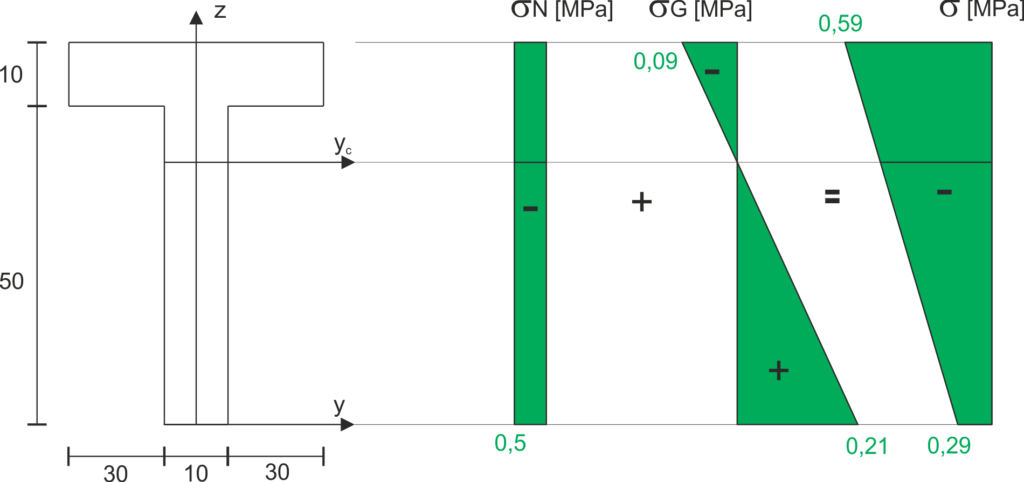
The final graph of normal stresses is obtained by adding compressive and tensile stresses at characteristic points (on the upper and lower fibers).
\begin{aligned}
z_{1} &=25 \mathrm{~mm} \\
z_{2} &=55 \mathrm{~mm} \\
A_{1} &=500 \mathrm{~mm}^{2} \\
A_{2} &=700 \mathrm{~mm}^{2} \\
z_{c} &=\frac{z_{1} \cdot A_{1}+z_{2} \cdot A_{2}}{A_{1}+A_{2}}=42.5 \mathrm{~mm} \\
I_{y c} &=\frac{10 \cdot 50^{3}}{12}+500 \cdot(25-42.5)^{2}+\frac{70 \cdot 10^{3}}{12}+700 \cdot(55-42.5)^{2}=372500 \mathrm{~cm}^{4} \\
\sigma_{G}^{d} &=\frac{18.225 \cdot 10^{3}}{372500 \cdot 10^{-8}} \cdot 0.0425=0.21 \mathrm{MPa} \\
\sigma_{G}^{g} &=\frac{18.225 \cdot 10^{3}}{372500 \cdot 10^{-8}} \cdot(0.06-0.0425)=-0.09 \mathrm{MPa}
\end{aligned}
The final graph of normal stresses is obtained by adding compressive and tensile stresses at characteristic points (on the upper and lower fibers).
If you have any questions, comments, or think you have found a mistake in this solution, please send us a message at kontakt@edupanda.pl.
