Solution
Classic version
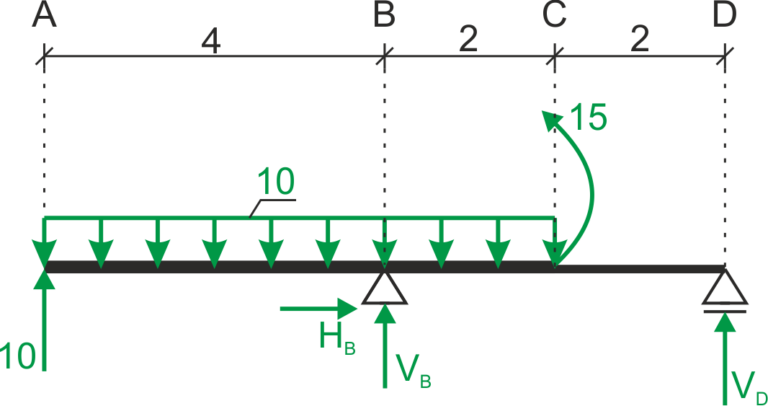
1. Marking characteristic points and reactions at supports
 \begin{aligned}
&\sum M_{D}=0 \\
&10 \cdot 8-60 \cdot 5-15+4 V_{B}=0 \\
&V_{B}=58.75 \mathrm{kN} \\
&\sum M_{B}=0 \\
&10 \cdot 4-60 \cdot 1-15-4 V_{D}=0 \\
&V_{D}=-8.75 \mathrm{kN} \\
&\sum Y=0 \\
&V_{B}+V_{D}-60+10=0 \\
&L=P
\end{aligned}
\begin{aligned}
&\sum M_{D}=0 \\
&10 \cdot 8-60 \cdot 5-15+4 V_{B}=0 \\
&V_{B}=58.75 \mathrm{kN} \\
&\sum M_{B}=0 \\
&10 \cdot 4-60 \cdot 1-15-4 V_{D}=0 \\
&V_{D}=-8.75 \mathrm{kN} \\
&\sum Y=0 \\
&V_{B}+V_{D}-60+10=0 \\
&L=P
\end{aligned}
3. Decomposition of internal force equations in individual variability intervals:
a)Interval AB 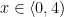
 \begin{aligned}
&Q_{A B}=10-10 \cdot x \\
&Q_{A(0)}=10 \\
&Q_{B(4)}=-30 \\
&M_{A B}=10 \cdot x-10 \cdot \frac{x^{2}}{2} \\
&M_{A(0)}=0 \\
&M_{B(4)}=-40
\end{aligned}
\begin{aligned}
&Q_{A B}=10-10 \cdot x \\
&Q_{A(0)}=10 \\
&Q_{B(4)}=-30 \\
&M_{A B}=10 \cdot x-10 \cdot \frac{x^{2}}{2} \\
&M_{A(0)}=0 \\
&M_{B(4)}=-40
\end{aligned}
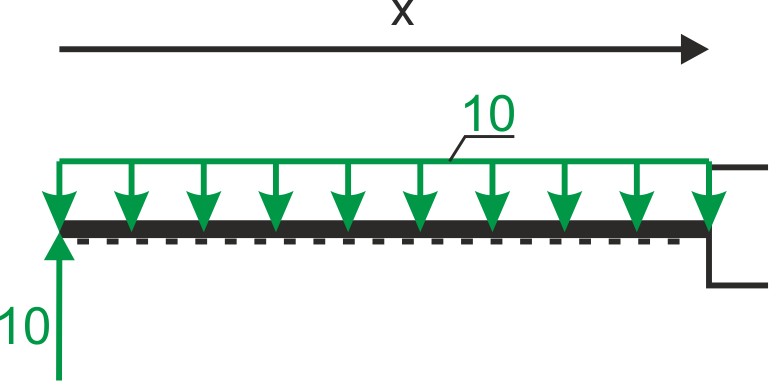
 \begin{aligned} \\ &Q_{AB}=10-10\cdot x=0\\ &10=10x\\ &x=1m\\ \\ \end{aligned}
\begin{aligned} \\ &Q_{AB}=10-10\cdot x=0\\ &10=10x\\ &x=1m\\ \\ \end{aligned}
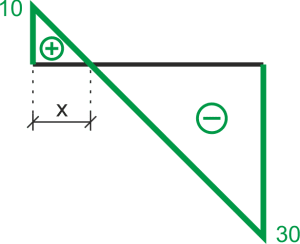
Extremum
\begin{aligned} \\ &\frac{10}{x}=\frac{30}{4-x} \ \Rightarrow \ x=1\\ &M_{max}=10\cdot 1 – 10\cdot(\frac{1}{2})^{2}=5\\ \\ \end{aligned}b) Interval BC 
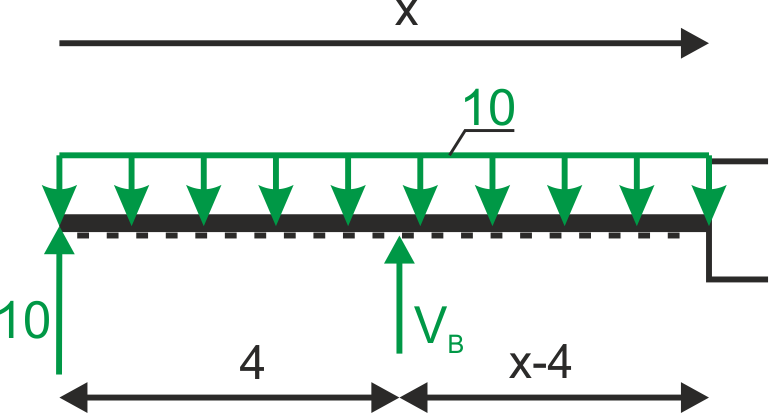
c) Interval DC 
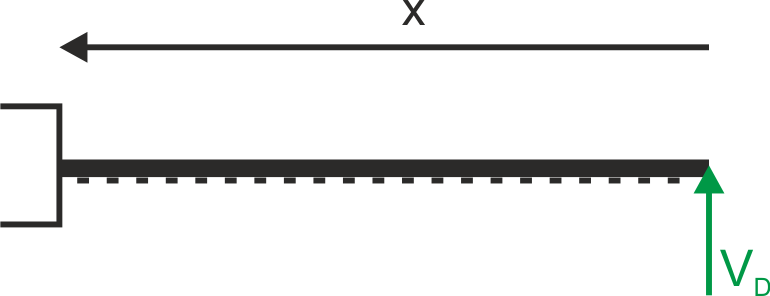
4. Final graphs
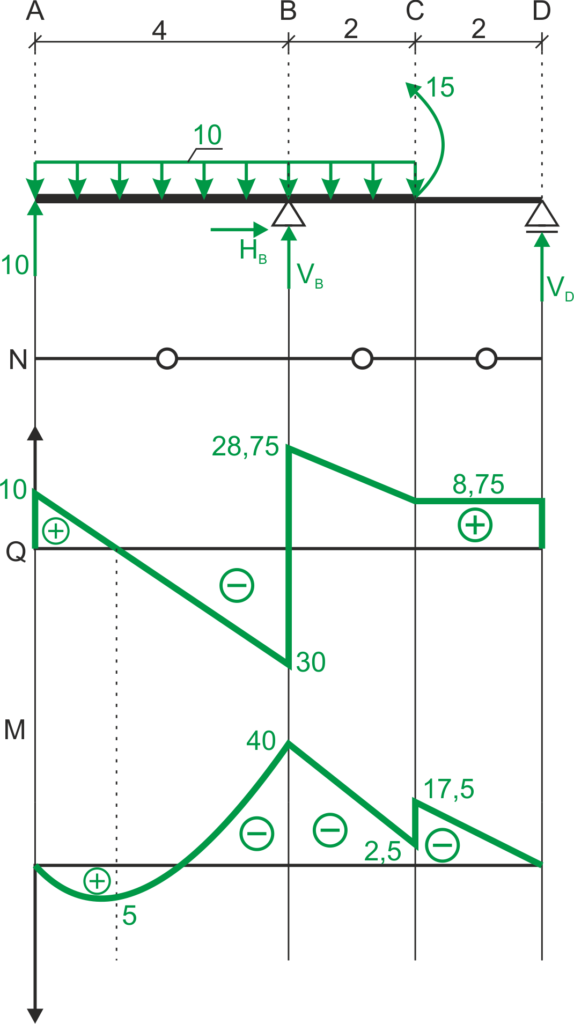
If you have any questions, comments, or think you have found a mistake in this solution, please send us a message at kontakt@edupanda.pl.
