The figure has two axes of symmetry, so the center of gravity lies at their intersection. Therefore, the marked y and z axes are the main central axes.

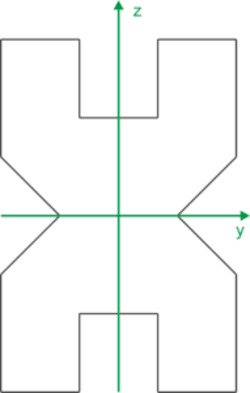
We calculate the main central moments of inertia.

\begin{aligned} &I_{YC}=\frac{12\cdot18^3}{12}-4\frac{3^4}{12}-2\cdot\Bigg[ \frac{4^4}{12}+4\cdot4\cdot(9-2)^2 \Bigg]=4194.33cm^4\\ &I_{ZC}=\frac{18\cdot12^3}{12}-2\Bigg[ \frac{3^3\cdot6}{36}+\frac{1}{2}\cdot3\cdot6\cdot(6-1)^2 \Bigg] - 2\cdot\frac{4^4}{12}=2090.33cm^4\\ \end{aligned}