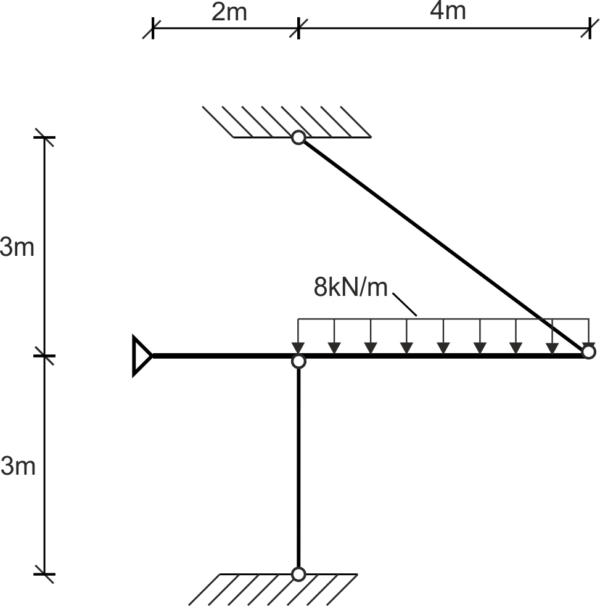
Solution
I mark the support reactions and forces in the truss bars
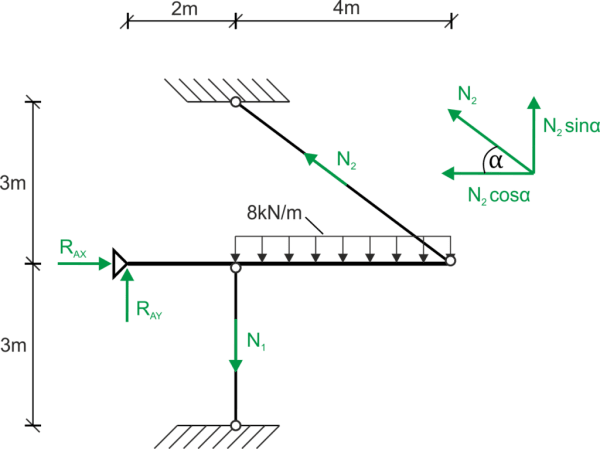
I write down one static equilibrium equation - one in which the unknowns are the forces \( N_1, N_2 \) in the bars: \begin{aligned} &\sum{M_{A}}=0\\ &N_{1}\cdot 2 - N_{2}\cdot \sin\alpha\cdot 6 + 8\cdot 4\cdot 4=0\\ &N_{1}=3N_{2}\cdot\sin\alpha - 64\\ &\sin\alpha=\frac{3}{5} & \cos\alpha=\frac{4}{5}\\ &N_{1}=1.8N_{2}-64\\ \end{aligned} I draw the displacement diagram in order to express the geometric condition (the relationship between displacements based on triangle similarity):
The bars can elongate in their axes, but the allowable line of displacement of the extended/shortened end of the bar is perpendicular to the axis of the bar.
Additionally, I remember that every point on the non-deformable horizontal beam can be found in the direction perpendicular to this axis.
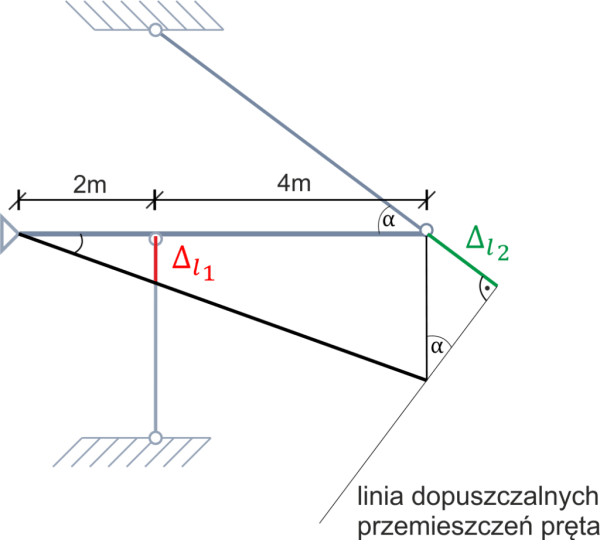
Geometric condition: \begin{aligned} &\frac{f_{B}}{2}=\frac{f_{A}}{6}\\ &\frac{\Delta l_{2}}{f_{A}}=\sin\alpha \ \ \ \Rightarrow \ \ \ f_{A}=\frac{\Delta l_{2}}{\sin\alpha}\\ &f_{B}=\Delta l_{1}\\ &\frac{\Delta l_{1}}{2}=\frac{\frac{\Delta l_{2}}{\sin\alpha}}{6}\\ &6\sin\alpha\cdot\Delta l_{1}=2\cdot\Delta l_{2}\\ &6\cdot 0.6\cdot\frac{-N_{1}\cdot 3}{E_{1}\cdot A_{1}}=2\cdot\frac{N_{2}\cdot 5}{E_{2}\cdot A_{2}}\\ &\frac{-10.8N_{1}}{2E_{2}\cdot A_{2}}=\frac{10N_{2}}{E_{2}\cdot A_{2}} \ \ \ \ \ \ \ \ |\cdot E_{2}A_{2}\\ &-5.4N_{1}=10N_{2}\\ &N_{1}=-1.85N_{2} \end{aligned} We obtain the second relationship between \(N_1\) and \(N_2\). We go back to the first relationship and calculate the forces in the bars:
\begin{aligned} &N_{1}=1.85N_{2}-64\\ &-1.85N_{2}=1.8N_{2}-64\\ \\ &N_{2}=17.53 \ kN\\ &N_{1}=-32.43 \ kN\\ \end{aligned} Strength condition: \begin{aligned} &\sigma=\frac{|N|}{A}\le k\\ \end{aligned} \begin{array}{ll} \sigma_{1}=\frac{32.43 \cdot 10^{3}}{A} \leq 90 \cdot 10^{6} & \Rightarrow A \geq 3.6 \cdot 10^{-4} \mathrm{~m}^{2} \\ \sigma_{2}=\frac{17.53 \cdot 10^{3}}{A} \leq 60 \cdot 10^{6} & \Rightarrow A \geq 2.92 \cdot 10^{-4} \mathrm{~m}^{2} \\ \end{array} The first condition is decisive, so I assume: \begin{array}{ll}A=3.65 \cdot 10^{-4} \mathrm{~m}^{2} & \Rightarrow d=0.0215 \mathrm{~m}=2.15 \mathrm{~cm} \\ A=\frac{\pi d^{2}}{4} \end{array}

I write down one static equilibrium equation - one in which the unknowns are the forces \( N_1, N_2 \) in the bars: \begin{aligned} &\sum{M_{A}}=0\\ &N_{1}\cdot 2 - N_{2}\cdot \sin\alpha\cdot 6 + 8\cdot 4\cdot 4=0\\ &N_{1}=3N_{2}\cdot\sin\alpha - 64\\ &\sin\alpha=\frac{3}{5} & \cos\alpha=\frac{4}{5}\\ &N_{1}=1.8N_{2}-64\\ \end{aligned} I draw the displacement diagram in order to express the geometric condition (the relationship between displacements based on triangle similarity):
The bars can elongate in their axes, but the allowable line of displacement of the extended/shortened end of the bar is perpendicular to the axis of the bar.
Additionally, I remember that every point on the non-deformable horizontal beam can be found in the direction perpendicular to this axis.

Geometric condition: \begin{aligned} &\frac{f_{B}}{2}=\frac{f_{A}}{6}\\ &\frac{\Delta l_{2}}{f_{A}}=\sin\alpha \ \ \ \Rightarrow \ \ \ f_{A}=\frac{\Delta l_{2}}{\sin\alpha}\\ &f_{B}=\Delta l_{1}\\ &\frac{\Delta l_{1}}{2}=\frac{\frac{\Delta l_{2}}{\sin\alpha}}{6}\\ &6\sin\alpha\cdot\Delta l_{1}=2\cdot\Delta l_{2}\\ &6\cdot 0.6\cdot\frac{-N_{1}\cdot 3}{E_{1}\cdot A_{1}}=2\cdot\frac{N_{2}\cdot 5}{E_{2}\cdot A_{2}}\\ &\frac{-10.8N_{1}}{2E_{2}\cdot A_{2}}=\frac{10N_{2}}{E_{2}\cdot A_{2}} \ \ \ \ \ \ \ \ |\cdot E_{2}A_{2}\\ &-5.4N_{1}=10N_{2}\\ &N_{1}=-1.85N_{2} \end{aligned} We obtain the second relationship between \(N_1\) and \(N_2\). We go back to the first relationship and calculate the forces in the bars:
\begin{aligned} &N_{1}=1.85N_{2}-64\\ &-1.85N_{2}=1.8N_{2}-64\\ \\ &N_{2}=17.53 \ kN\\ &N_{1}=-32.43 \ kN\\ \end{aligned} Strength condition: \begin{aligned} &\sigma=\frac{|N|}{A}\le k\\ \end{aligned} \begin{array}{ll} \sigma_{1}=\frac{32.43 \cdot 10^{3}}{A} \leq 90 \cdot 10^{6} & \Rightarrow A \geq 3.6 \cdot 10^{-4} \mathrm{~m}^{2} \\ \sigma_{2}=\frac{17.53 \cdot 10^{3}}{A} \leq 60 \cdot 10^{6} & \Rightarrow A \geq 2.92 \cdot 10^{-4} \mathrm{~m}^{2} \\ \end{array} The first condition is decisive, so I assume: \begin{array}{ll}A=3.65 \cdot 10^{-4} \mathrm{~m}^{2} & \Rightarrow d=0.0215 \mathrm{~m}=2.15 \mathrm{~cm} \\ A=\frac{\pi d^{2}}{4} \end{array}
If you have any questions, comments, or think you have found a mistake in this solution, please send us a message at kontakt@edupanda.pl.