Rozwiązanie
Rozwiązanie wideo
Rozwiązanie klasyczne
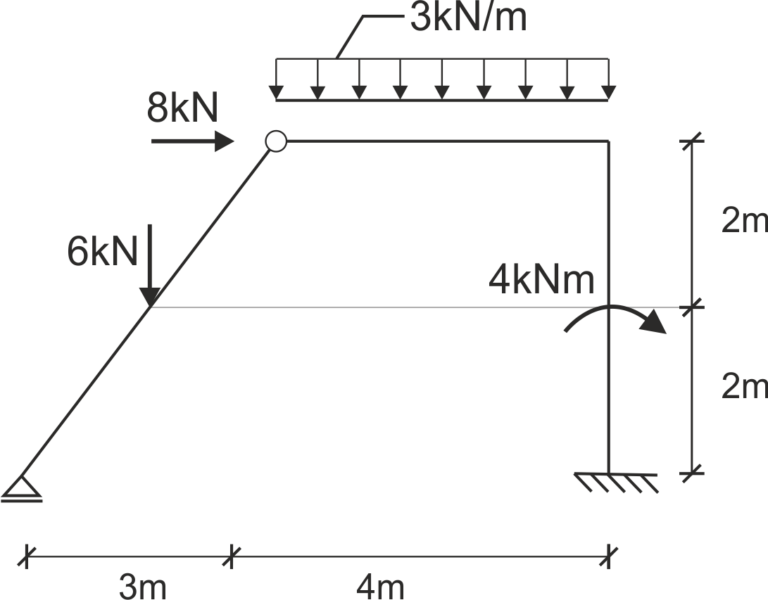
Opisanie punktów charakterystycznych,
| \( \quad \quad \) |
Obliczenie reakcji\begin{aligned} &\sum M_{C}^L = 0\\ &-6 \cdot \frac{3}{2} + V_{A} \cdot 3 = 0\\ &V_{A} = \frac{6 \cdot \frac{3}{2}}{3} = 3 \, \text{kN}\\ \\ &\Sigma X = 0\\ &8 + H_{F} = 0\\ &H_{F} = -8 \, \text{kN}\\ \\ &\Sigma Y = 0\\ &V_{A} - 6 - 3 \cdot 4 + V_{F} = 0\\ &V_{F} = -\left(V_{A} - 6 - 3 \cdot 4\right) = 15 \, \text{kN}\\ \\ &\Sigma M_{A} = 0\\ &6 \cdot \frac{3}{2} + 8 \cdot 4 + 3 \cdot 4 \cdot 5 + 4 - V_{F} \cdot 7 + M_{F} = 0\\ &M_{F} = -\left(6 \cdot \frac{3}{2} + 8 \cdot 4 + 3 \cdot 4 \cdot 5 + 4 - V_{F} \cdot 7\right) = 0 \, \text{kNm} \end{aligned} |
Przedział AB \( 0 \leq x \leq 1.5\)

| \( \quad \quad \) |
\begin{aligned}
&Q(x) = 3 \cos (\alpha) = 1.8 \, \text{kN} \\
&M(x) = 3x \\
&M(0) = 0 \\
&M(1.5) = 4.5 \, \text{kNm} \\
&N(x) = 3 \sin (\alpha) = -2.4 \, \text{kN}
\end{aligned}
|
Przedział BC \( 1.5 \leq x \leq 3\)

| \( \quad \quad \) |
\begin{aligned}
&Q(x) = 3 \cos (\alpha) - 6 \cos (\alpha) = -1.8 \, \text{kN} \\
&M(x) = 3x - 6 \cdot(x - 1.5) \\
&M(1.5) = 4.5 \, \text{kNm} \\
&M(3) = 0 \\
&N(x) = 3 \sin (\alpha) + 6 \sin (\alpha) = -2.4 \, \text{kN}
\end{aligned}
|
Przedział CD \( 0 \leq x \leq 4\)
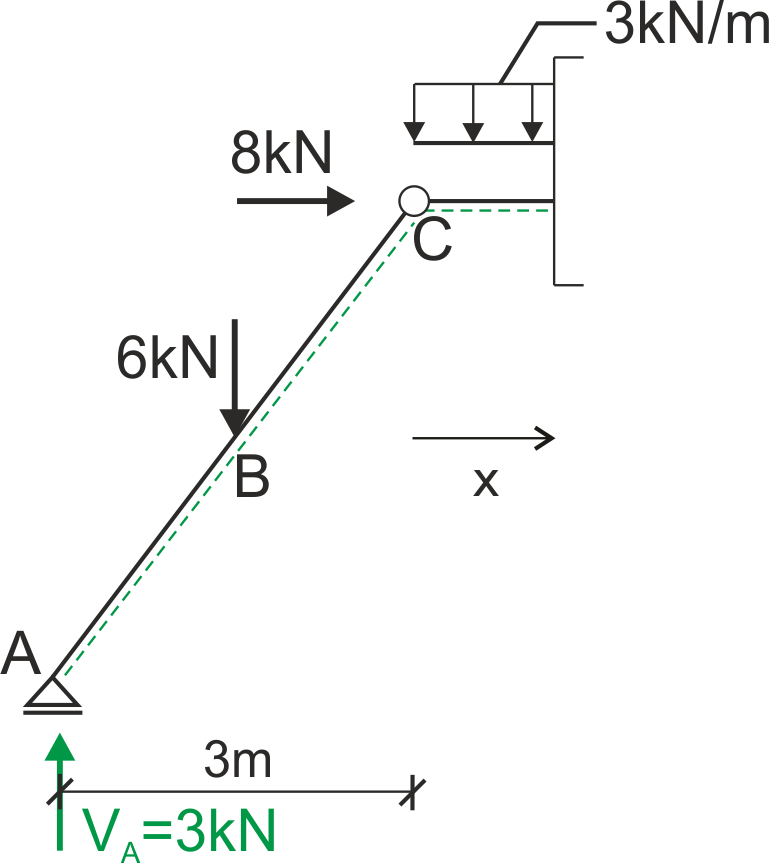
| \( \quad \quad \) |
\begin{aligned}
& \mathrm{N}(\mathrm{x})=-8 \ \mathrm{kN} \\
& \mathrm{Q}(\mathrm{x})=3-6-3 \cdot \mathrm{x}=-3 \cdot \mathrm{x}-3 \\
& \mathrm{Q}(0)=-3 \ \mathrm{kN} \\
& \mathrm{Q}(4)=-15 \ \mathrm{kN} \\
& \mathrm{M}(\mathrm{x})=3 \cdot(3+\mathrm{x})-6 \cdot(1.5+\mathrm{x})-3 \cdot \mathrm{x} \cdot \frac{\mathrm{x}}{2} \\
& \mathrm{M}(0)=0 \ \mathrm{kNm} \\
& \mathrm{M}(4)=-36 \ \mathrm{kNm}
\end{aligned}
|
Przedział FE \( 0 \leq x \leq 2\)
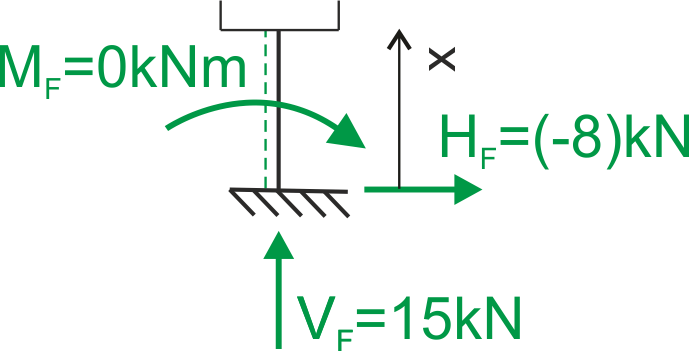
| \( \quad \quad \) |
\begin{aligned}
& \mathrm{N}(\mathrm{x})=-15 \ \mathrm{kN} \\
& \mathrm{Q}(\mathrm{x})=8 \ \mathrm{kN} \\
& \mathrm{M}(\mathrm{x})=-8 \cdot \mathrm{x} \\
& \mathrm{M}(0)=0 \\
& \mathrm{M}(2)=-16 \ \mathrm{kNm}
\end{aligned}
|
Przedział ED \( 2 \leq x \leq 4\)
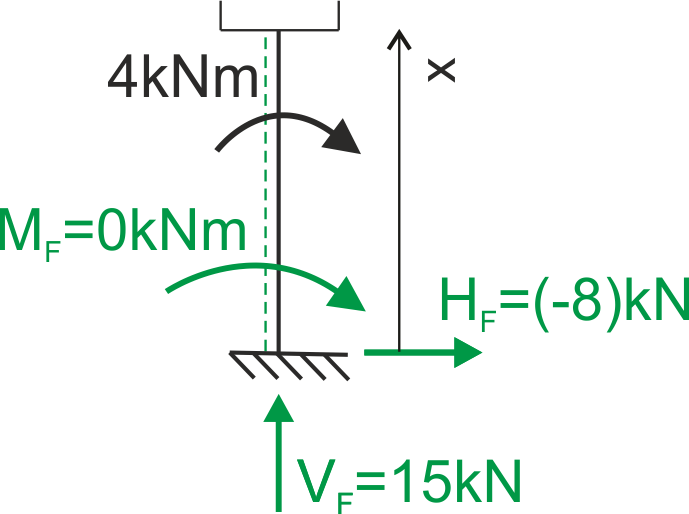
| \( \quad \quad \) |
\begin{aligned}
& \mathrm{N}(\mathrm{x})=-15 \ \mathrm{kN} \\
& \mathrm{Q}(\mathrm{x})=8 \ \mathrm{kN} \\
& \mathrm{M}(\mathrm{x})=-8 \cdot \mathrm{x}-4 \\
& \mathrm{M}(2)=-20 \ \mathrm{kNm} \\
& \mathrm{M}(4)=-36 \ \mathrm{kNm}
\end{aligned}
|
Wykresy



Równowaga węzła C

| \( \quad \quad \) | \begin{aligned} &\Sigma X = 0\\ &8 - 8 - 2.4 \cdot \cos (\alpha) + 1.8 \cdot \sin (\alpha) = 0\\ &L = P\\ &\Sigma Y = 0\\ &3 - 2.4 \cdot \sin (\alpha) + 1.8 \cdot \cos (\alpha) = 0\\ &L = P \end{aligned} |
Jeżeli masz jakieś pytania, uwagi lub wydaje Ci się, że znalazłeś błąd w tym rozwiązaniu, napisz proszę do nas wiadomość na kontakt@edupanda.pl lub skontaktuj się z nami przez nasz profil na FB: