Rozwiązanie
Przeliczenie momentu skręcającego zgodnie ze wzorem \(M_s=9550\cdot \frac{N [kW]}{n [obr/min]} M_s=9550\cdot \frac{10}{955}=100 Nm\)
Siła F na ramieniu połowy koła pasowego odbiera moment skręcający który jest nadawany przez silnik na początku wału. Moment skręcający powstaje między silnikiem a kołem pasowym. Obliczamy siłę F na kole pasowym.
\begin{aligned} &F\cdot 0,2=100\Rightarrow F=500 N\\ \end{aligned}Mamy do czynienia ze zginaniem wału w jednej płaszczyźnie oraz skręcaniem.
Wykres momentu skręcającego oraz schemat do liczenia momentu gnącego.
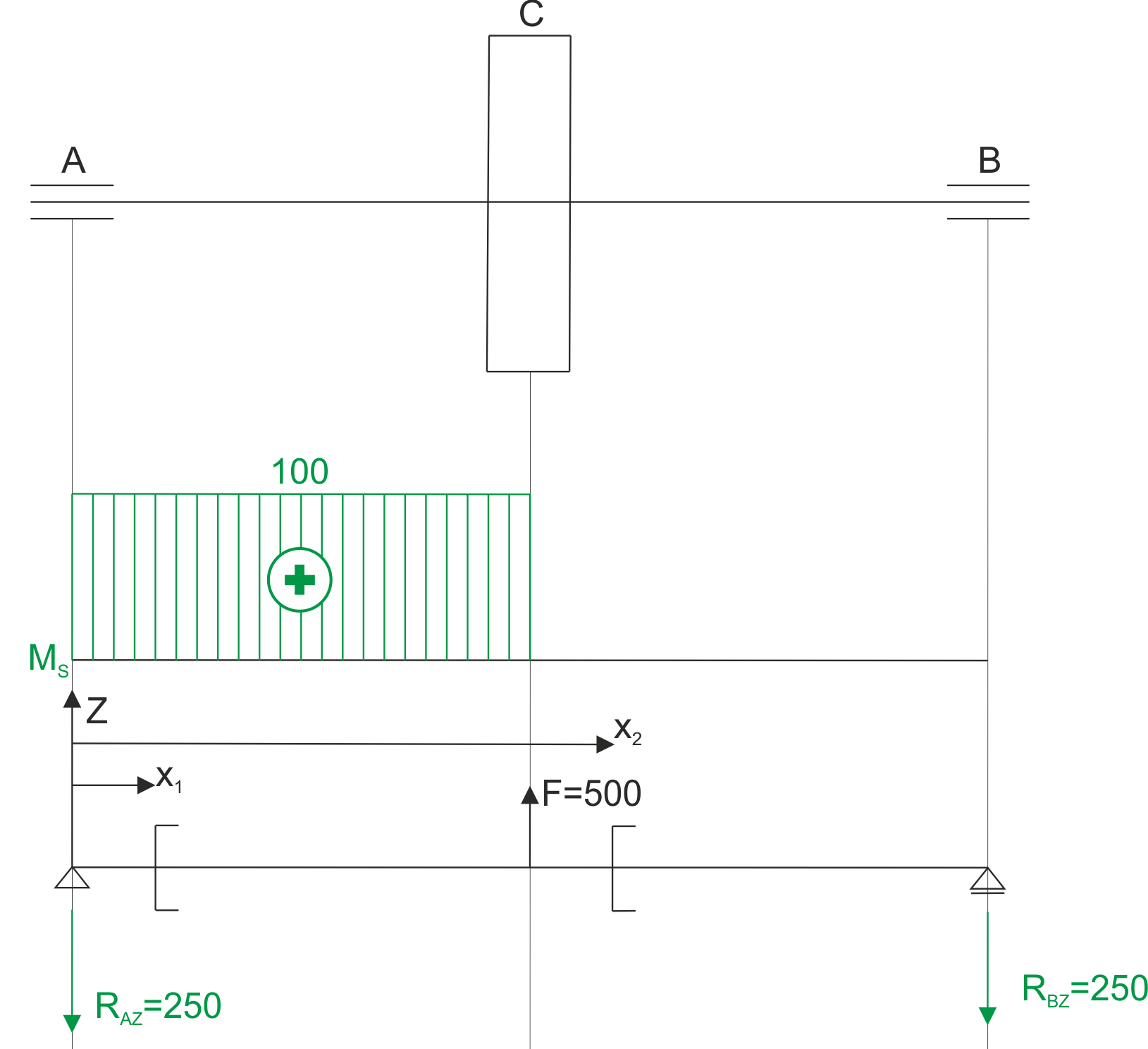 \begin{aligned}
&x_{1} \in(0 ; 0,5) \\
&M\left(x_{1}\right)=-R_{A Z} \cdot x_{1} \\
&M(0)=0 N m \\
&M(0,5)=-125 N m \\
&x_{2} \in(0,5 ; 1) \\
&M\left(x_{1}\right)=-R_{A Z} \cdot x_{2}+500 \cdot\left(x_{2}-0,5\right) \\
&M(0,5)=-125 N m \\
&M(1)=0 N m
\end{aligned}
\begin{aligned}
&x_{1} \in(0 ; 0,5) \\
&M\left(x_{1}\right)=-R_{A Z} \cdot x_{1} \\
&M(0)=0 N m \\
&M(0,5)=-125 N m \\
&x_{2} \in(0,5 ; 1) \\
&M\left(x_{1}\right)=-R_{A Z} \cdot x_{2}+500 \cdot\left(x_{2}-0,5\right) \\
&M(0,5)=-125 N m \\
&M(1)=0 N m
\end{aligned}
Wykres momentu gnącego.
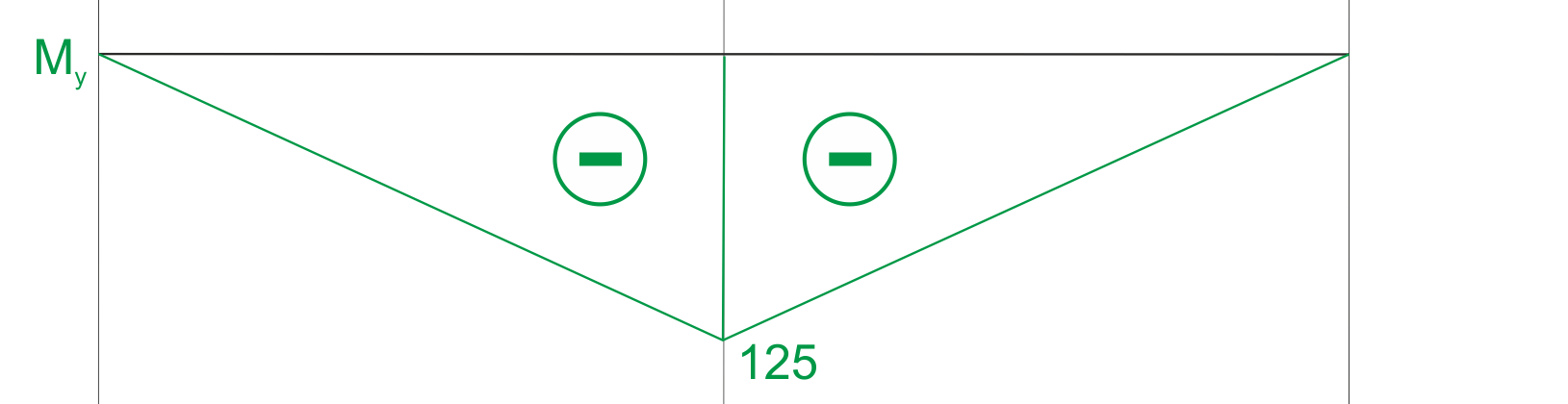
Liczymy wartość momentu zastępczego w punktach charakterystycznych.
\begin{aligned} &M_{z a s}=\sqrt{M_{g}^{2}+\frac{3}{4} M_{s}^{2}} \\ &M_{z a s}^{A}=\sqrt{0^{2}+\frac{3}{4} \cdot 100^{2}}=86,6 \mathrm{Nm} \\ &M_{z a s}^{C A}=\sqrt{125^{2}+\frac{3}{4} \cdot 100^{2}}=152,1 \mathrm{Nm} \\ &M_{z a s}^{C B}=\sqrt{125^{2}+\frac{3}{4} \cdot 0^{2}}=125 \mathrm{Nm} \\ &M_{z a s}^{B}=\sqrt{0^{2}+\frac{3}{4} \cdot 0^{2}}=0 \mathrm{Nm} \end{aligned}Wykres momentu zastępczego
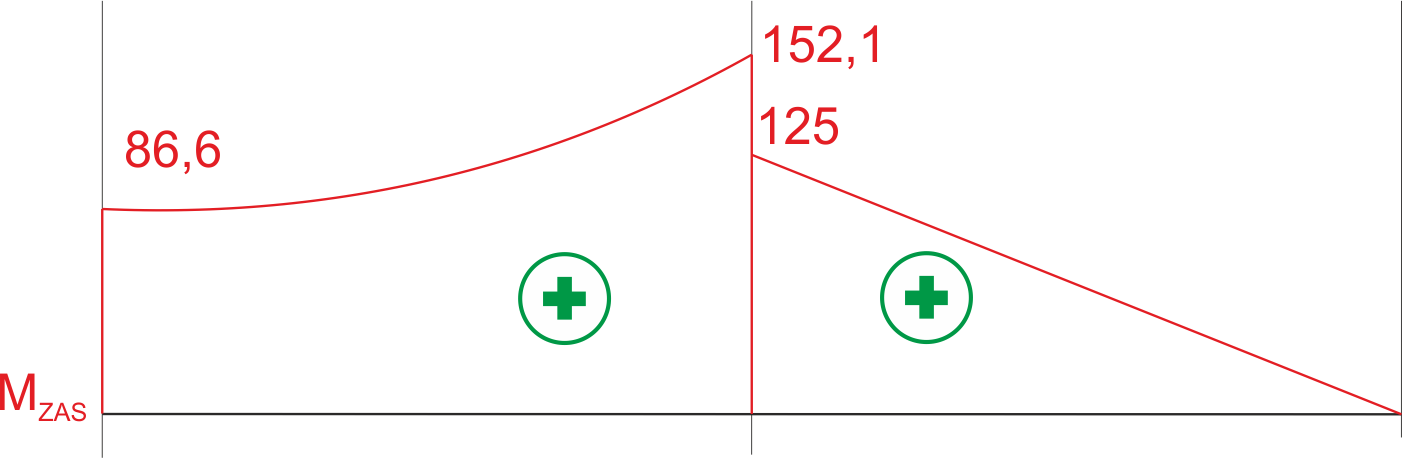
Wymiarujemy wał na maksymalny moment zastępczy. Korzystamy w wyprowadzonego wzoru
\begin{aligned} &M_{z a s}^{\max }=152,1 \mathrm{Nm} \\ &d \geq \sqrt[3]{\frac{32 M_{z a s}}{\pi \cdot k_{g}}} \\ &d \geq 0,0295 \mathrm{~m} \\ &d=3 \mathrm{~cm} \end{aligned}