Wykresy w belkach
Z tego tekstu dowiesz się czym jest siła osiowa (inaczej normalna), siła poprzeczna (inaczej tnąca)
i moment gnący oraz jaka jest konwencja znakowania tych sił wewnętrznych.
Opiszemy jakie są zależności między obciążeniem ciągłym, siłą tnącą i momentem gnącym oraz jakich zmian na wykresach sił wewnętrznych należy się spodziewać przy określonym obciążeniu na belce.
Oto, jak zazwyczaj wygląda konwencja znakowania dla każdej z sił wewnętrznych:

1. Siła normalna (N)
2. Siła poprzeczna (Q)
3. Moment zginający (M)
Zależność między:
Może być ono stałe lub zmienne w zależności od położenia x na belce.
\( \frac{dQ(x)}{dx} = -q(x) \)
Innymi słowy, zmiana siły tnącej wzdłuż belki jest spowodowana obciążeniem ciągłym.
\( \frac{dM(x)}{dx} = Q(x) \)
Zatem zmiana momentu zginającego wzdłuż belki jest spowodowana siłą tnącą.
1) Podstawową metodą rysowania wykresów sił wewnętrznych jest pierwotne zapisanie funkcji sił wewnętrznych. W naszych kursach, również darmowych, znajdziesz przykłady od początku do końca rozwiązania belki tą metodą.
2) Bardziej zaawansowana metoda polega na rysowaniu wykresów bez zapisywania funkcji sił wewnętrznych i do tej metody przyda się znajomość pewnych zasad rysowania wykresów sił wewnętrznych:
3) Ciekawą zależność między wykresem Q(x) i M(x) a mianowicie, że na wykresie momentów gnących mamy zmianę odpowiadającą polu z wykresu sił tnących również można wykorzystać do rysowania wykresów, obliczenia wykorzystujące tą metodą również znajdziecie w naszych materiałach na YouTube, jednak jest to metoda rzadko pokazywana przez prowadzących zajęcia.
Teoria teorią, ale jednak lepsze zrozumienie przyniesie na pewno rozwiązanie przykładów:
Kurs wideo pokazujący jak określać skoki na wykresach
Opiszemy jakie są zależności między obciążeniem ciągłym, siłą tnącą i momentem gnącym oraz jakich zmian na wykresach sił wewnętrznych należy się spodziewać przy określonym obciążeniu na belce.
Obliczanie belek
Rodzaje sił wewnętrznych
Mamy trzy podstawowe rodzaje sił wewnętrznych, które mogą występować w belkach:
1. Siły normalne (osiowe) - wynikają z działania sił wzdłuż osi belki. Jeżeli siła jest skierowana wzdłuż osi belki, powodując jej rozciąganie lub ściskanie, to jest to siła normalna. Symbolicznie oznaczane jako N.
2. Siły poprzeczne (tnące) - działają prostopadle do osi belki i powodują wewnętrzne naprężenia ścinające. Oznaczane są jako Q i są odpowiedzialne za przesunięcie pionowe różnych przekrojów belki względem siebie.
3. Moment zginający - to moment siły, który powoduje zginanie belki. Wpływa na krzywiznę belki i zmienia się wzdłuż jej długości. Moment zginający oznaczamy jako M.
2. Siły poprzeczne (tnące) - działają prostopadle do osi belki i powodują wewnętrzne naprężenia ścinające. Oznaczane są jako Q i są odpowiedzialne za przesunięcie pionowe różnych przekrojów belki względem siebie.
3. Moment zginający - to moment siły, który powoduje zginanie belki. Wpływa na krzywiznę belki i zmienia się wzdłuż jej długości. Moment zginający oznaczamy jako M.
Konwencja znakowania sił wewnętrznych
Konwencja znakowania sił wewnętrznych w mechanice belki jest kluczowa, aby prawidłowo interpretować ich kierunki i wartości, a także spójnie zapisywać wyniki w analizie konstrukcji.Oto, jak zazwyczaj wygląda konwencja znakowania dla każdej z sił wewnętrznych:

Rys1. Konwencja znakowania sił wewnętrznych
1. Siła normalna (N)
- Rozciąganie: Siła, która rozciąga belkę (działa na zewnątrz przekroju, "oddala" się od środka belki), jest zazwyczaj uznawana za dodatnią. W skrócie: jeżeli belka jest rozciągana, siła normalna N jest dodatnia.
- Ściskanie: Siła, która ściska belkę (działa w kierunku osiowym, do środka przekroju, powodując ściskanie), jest uznawana za ujemną.
- Ściskanie: Siła, która ściska belkę (działa w kierunku osiowym, do środka przekroju, powodując ściskanie), jest uznawana za ujemną.
2. Siła poprzeczna (Q)
- Dodatnia siła tnąca: Gdy siła działa w górę po lewej stronie przekroju lub w dół po prawej stronie przekroju, siła poprzeczna jest uznawana za dodatnią.
- Ujemna siła tnąca: Siła działająca w dół po lewej stronie przekroju lub w górę po prawej stronie przekroju jest uznawana za ujemną.
- Ujemna siła tnąca: Siła działająca w dół po lewej stronie przekroju lub w górę po prawej stronie przekroju jest uznawana za ujemną.
3. Moment zginający (M)
- Dodatni moment zginający (momenty powodujące uśmiech): Jeżeli moment zginający powoduje, że belka wygina się w kształt przypominający "uśmiech" (tzn. włókna górne belki są ściskane, a dolne rozciągane), moment jest dodatni.
- Ujemny moment zginający (momenty powodujące smutną minę): Gdy belka wygina się w przeciwnym kierunku (włókna górne rozciągane, a dolne ściskane – "smutna mina"), moment zginający jest ujemny.
- Ujemny moment zginający (momenty powodujące smutną minę): Gdy belka wygina się w przeciwnym kierunku (włókna górne rozciągane, a dolne ściskane – "smutna mina"), moment zginający jest ujemny.
Zależność między:
obciążeniem ciągłym <-> siłą tnącą <-> momentem gnącym
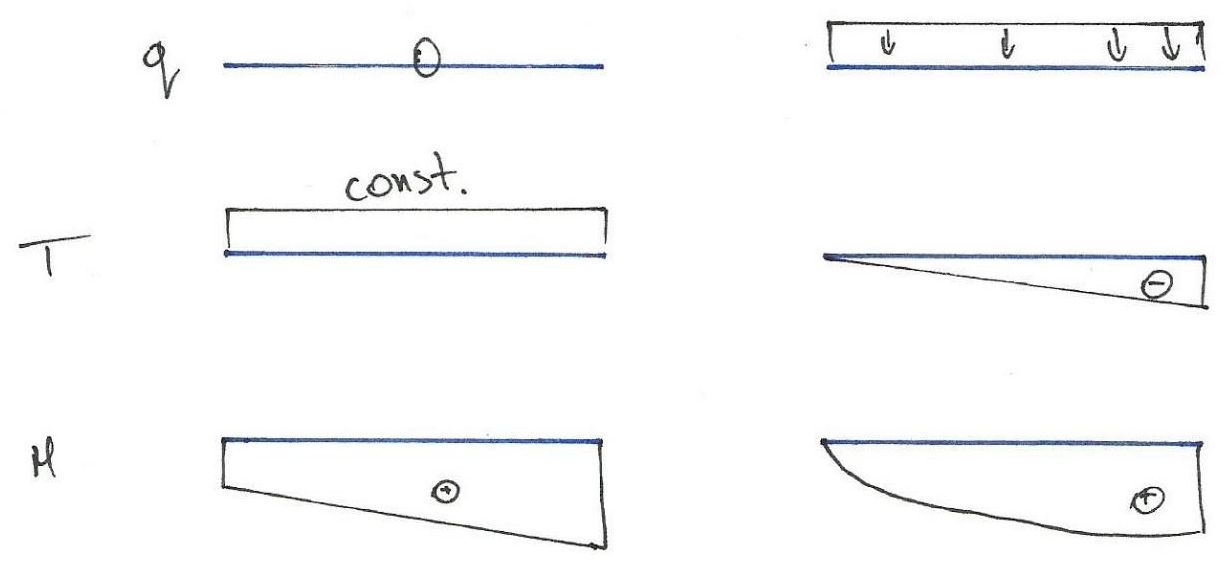
1. Obciążenie ciągłe q(x)
Obciążenie ciągłe q(x) to siła rozłożona wzdłuż długości belki, działająca na jednostkę długości.Może być ono stałe lub zmienne w zależności od położenia x na belce.
2. Siła tnąca Q(x)
Związek między obciążeniem ciągłym a siłą tnącą:\( \frac{dQ(x)}{dx} = -q(x) \)
Innymi słowy, zmiana siły tnącej wzdłuż belki jest spowodowana obciążeniem ciągłym.
- Gdy obciążenie ciągłe q(x) jest dodatnie (np. skierowane w dół), siła tnąca Q(x) maleje wzdłuż długości belki.
- Gdy q(x) = 0 (brak obciążenia), siła tnąca jest stała.
- Jeśli siła tnąca jest zerowa - wówczas moment gnący jest stały.
- Gdy q(x) = 0 (brak obciążenia), siła tnąca jest stała.
- Jeśli siła tnąca jest zerowa - wówczas moment gnący jest stały.
3. Moment zginający M(x)
Związek między siłą tnącą a momentem zginającym:\( \frac{dM(x)}{dx} = Q(x) \)
Zatem zmiana momentu zginającego wzdłuż belki jest spowodowana siłą tnącą.
- Gdy siła tnąca Q(x) jest dodatnia, moment zginający M(x) wzrasta.
- Gdy wykres sił tnących Q(x) = 0, moment zginający osiąga ekstremum.
- Gdy wykres sił tnących Q(x) = 0, moment zginający osiąga ekstremum.

Rys2. Zależność: obciążenie ciągłe - siła tnąca - moment gnący
Zasady rysowania wykresów sił wewnętrznych
Powiedzmy że są trzy metody rysowania wykresów sił wewnętrznych:1) Podstawową metodą rysowania wykresów sił wewnętrznych jest pierwotne zapisanie funkcji sił wewnętrznych. W naszych kursach, również darmowych, znajdziesz przykłady od początku do końca rozwiązania belki tą metodą.
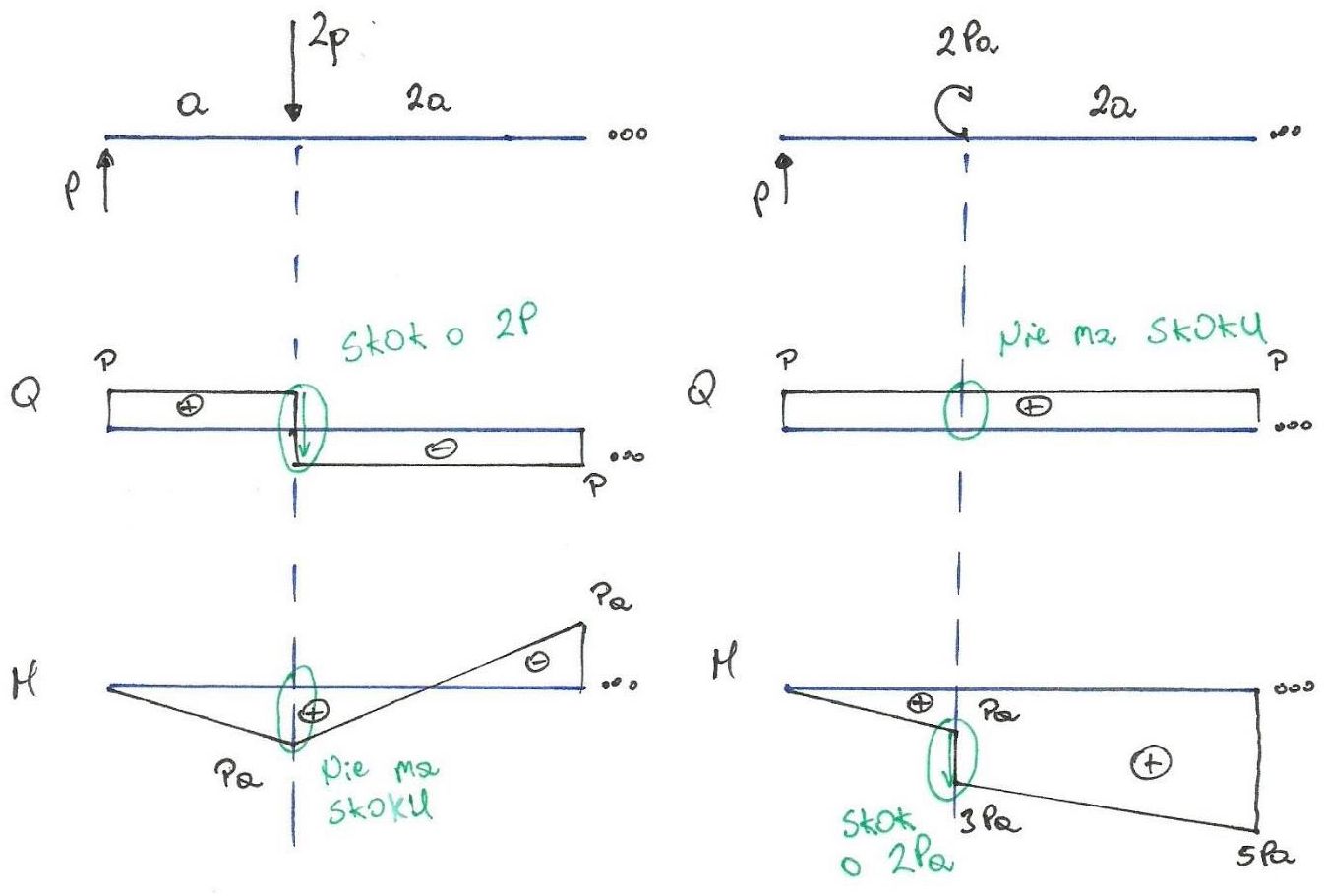
2) Bardziej zaawansowana metoda polega na rysowaniu wykresów bez zapisywania funkcji sił wewnętrznych i do tej metody przyda się znajomość pewnych zasad rysowania wykresów sił wewnętrznych:
- jeżeli w dowolnym punkcie belki jest przyłożona siła poprzeczna, na wykresie sił poprzecznych Q następuje skok o wartość tej siły,
skok jest w tą stronę co zwrot siły patrząc na wykres od lewej do prawej strony,
- jeżeli na odcinku belki występuje obciążenie ciągłe, to na wykresie sił poprzecznych Q na tym odcinku następuje zmiana o wartość wypadkowej
od obciążenia ciągłego ze zwrotem zgodnym z wypadkową (patrząc na wykres od lewej do prawej strony),
- jeżeli w dowolnym punkcie belki jest przyłożony moment skupiony, to na wykresie momentów M następuje skok o wartość tego momentu,
skok jest w stronę dodatnią lub ujemną w zależności czy jest prawoskrętny, czy lewoskrętny - patrz konwencja znakowania
skok jest w tą stronę co zwrot siły patrząc na wykres od lewej do prawej strony,
- jeżeli na odcinku belki występuje obciążenie ciągłe, to na wykresie sił poprzecznych Q na tym odcinku następuje zmiana o wartość wypadkowej
od obciążenia ciągłego ze zwrotem zgodnym z wypadkową (patrząc na wykres od lewej do prawej strony),
- jeżeli w dowolnym punkcie belki jest przyłożony moment skupiony, to na wykresie momentów M następuje skok o wartość tego momentu,
skok jest w stronę dodatnią lub ujemną w zależności czy jest prawoskrętny, czy lewoskrętny - patrz konwencja znakowania

Rys3. Obciążenie na belce a skoki na wykresach Q i M
3) Ciekawą zależność między wykresem Q(x) i M(x) a mianowicie, że na wykresie momentów gnących mamy zmianę odpowiadającą polu z wykresu sił tnących również można wykorzystać do rysowania wykresów, obliczenia wykorzystujące tą metodą również znajdziecie w naszych materiałach na YouTube, jednak jest to metoda rzadko pokazywana przez prowadzących zajęcia.
Teoria teorią, ale jednak lepsze zrozumienie przyniesie na pewno rozwiązanie przykładów:
Kurs wideo pokazujący jak określać skoki na wykresach
oraz opisujący metodę 2) i 3) rysowania wykresów na 4 przykładach.
Zestaw 19 belek z krótkimi rozwiązaniami
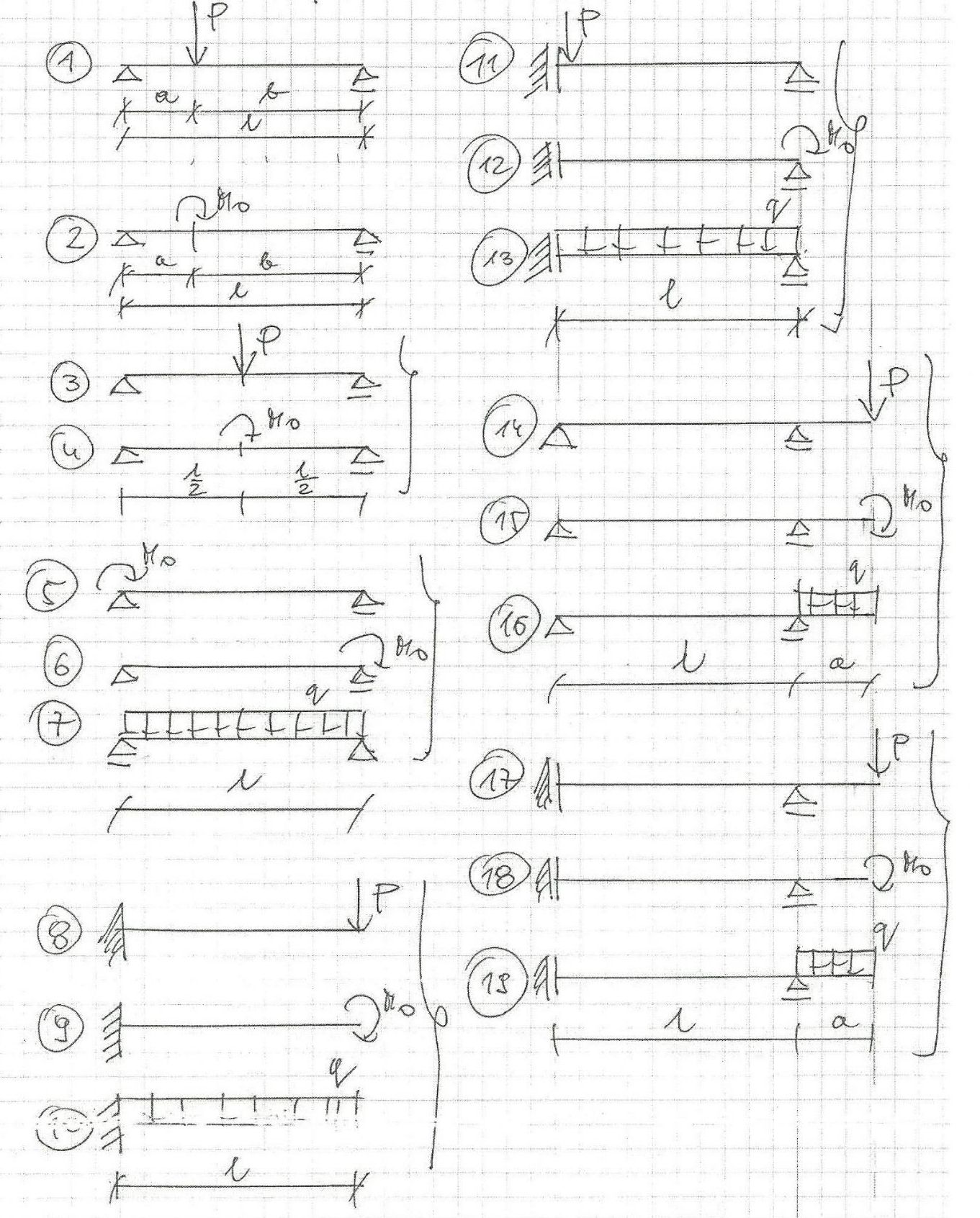
Poniżej krótkie rozwiązania + wykresy dla każdej belki
Rozwiązania












Poniżej znajdziesz również odnośniki do licznych przykładów rozwiązania zarówno belek prostych jak i skośnych, a także przegubowych.
ZOBACZ TEŻ

