Wytrzymałość materiałów - Metoda trzech momentów
Metoda trzech momentów, znana również jako metoda Clapeyrona, jest techniką stosowaną do rozwiązywania belek ciągłych (belki wieloprzęsłowe) statycznie niewyznaczalnych. Metoda ta bazuje na równaniach równowagi momentów zginających, sformułowanych dla trzech kolejnych podpór w belce ciągłej.
Podstawowym założeniem metody trzech momentów jest wykorzystanie zależności geometrycznych i statycznych między momentami zginającymi na trzech kolejnych podporach oraz obciążeniami działającymi na sąsiadujące przęsła belki. Metoda ta pozwala na wyznaczenie wartości momentów podporowych bez konieczności szczegółowego analizowania wszystkich sił reakcji.
Korzystając z metody trzech momentów, formułuje się równania opisujące warunki ciągłości ugięć i kątów obrotu na podporach pośrednich. Dla belki o wielu przęsłach powstaje układ równań liniowych, w którym niewiadomymi są momenty podporowe. Rozwiązanie tego układu umożliwia dalsze określenie rozkładu momentów, sił poprzecznych oraz ugięć w całej belce.
Zaletą metody trzech momentów jest jej stosunkowo prosta i systematyczna procedura obliczeniowa, szczególnie efektywna dla belek wieloprzęsłowych o dowolnej liczbie przęseł i różnorodnych schematach obciążeń.
Algorytm rozwiązania
-
Ustalenie schematu statycznego belki:
- Określ liczbę podpór i przęseł.
- Zidentyfikuj podpory (skrajne, pośrednie) i przypisz im odpowiednie numery lub symbole.
-
Określenie parametrów geometrycznych belki:
- Wyznacz długości kolejnych przęseł \( l_n, l_{n+1}, \ldots \).
- Określ sztywności poszczególnych przęseł belki (stała lub zmienna sztywność EI).
-
Narysowanie wykresów momentów dla zadanego obciążenia:
- Dla każdego przęsła obciążonego wyznacz wykres momentów.
-
Rozwiązanie belek wtórnych:
- Tutaj można do sprawy podejść na dwa sposoby:
- 1) Oblicz reakcje przy podporze pośredniej dla dwóch sąsiadujących belek \( R_{N1}, R_{Np} \) - reakcje na podporze "n" z lewej strony i reakcja na podporze "n" z prawej strony. Obciążeniem belki wtórnej dla której wyznaczamy reakcje jest wykres momentów z belki pierwotnej zamieniony na obciążenie ciągłe.
- 2) Oblicz kąt obrotu przy podporze pośredniej dla jednej i drugiej sąsiadującej belki - czyli przecałkuj wykresy momentów które powstały w stanie pierwotnym oraz w stanie od jednostkowych momentów na podporze pośredniej. Całkowanie można to przeprowadzić np. obliczając pole na wykresach na obu belkach, czyli: \( \Omega_n, \Omega_{n+1} \) oraz położenie ich środków ciężkości \( a_n, b_{n+1} \)
-
Formułowanie układu równań metody trzech momentów:
- Zastosuj wzory metody trzech momentów (Clapeyrona), zestawiając je dla kolejnych trzech podpór.
- Dla belki z \( n \) podporami \( (n-2) \) równania liniowe z niewiadomymi momentami podporowymi.
-
Rozwiązanie układu równań:
- Rozwiąż otrzymany układ równań liniowych względem niewiadomych momentów podporowych \( M_{n-1}, M_n, M_{n+1} \).
-
Obliczenie reakcji podporowych i sił poprzecznych:
- Korzystając z uzyskanych momentów podporowych, wyznacz reakcje na podporach oraz siły tnące w poszczególnych przęsłach belki.
-
Wyznaczenie wykresów momentów zginających i sił tnących:
- Sporządź wykres momentów zginających, wykorzystując obliczone momenty podporowe oraz wpływ obciążeń w przęsłach.
- Wyznacz wykres sił tnących na podstawie wcześniej wyznaczonych reakcji podporowych.
Równanie trzech momentów
Dla belek o stałej sztywności
\begin{aligned} M_{n-1} l_{n}+2 M_{n}\left(l_{n}+l_{n+1}\right)+M_{n+1} l_{n+1}=-6\left(R_{N l}+R_{N} p\right) \end{aligned}Dla belek o zmiennej sztywności
\begin{aligned} c M_{n-1} l_{n}+2 M_{n}\left(c l_{n}+l_{n+1}\right)+M_{n+1} l_{n+1}=-6\left(c R_{N l}+R_{N} p\right) \end{aligned}Można również spotkać zapis postaci
\begin{aligned} c M_{n-1} l_{n}+2 M_{n}\left(c l_{n}+l_{n+1}\right)+M_{n+1} l_{n+1}=-6 c \frac{\Omega_{n} a_{n}}{l_{n}}-6 \frac{\Omega_{n+1} b_{n+1}}{l_{n+1}} \end{aligned} Legenda do wzorów:- \(M_{n-1}, M_n, M_{n+1}\) - momenty zginające na kolejnych podporach (poprzedniej, bieżącej i nastẹpnej)
- \(l_n, l_{n+1}\) - długości kolejnych przęseł belki
- \(R_N, R_{N p}\) - wielkości zależne od rodzaju i rozkładu obciążeń na przęsłach (momenty zastępcze wynikające z obciążeń)
- \(c\) - współczynnik uwzglẹdniający zmienność sztywności belki; \[ c = \frac{(EI)_{n+1}}{(EI)_n} \] - \(\Omega_n, \Omega_{n+1}\) - pola wykresów momentów od obciążeń na poszczególnych przęsłach
- \(a_n, b_{n+1}\) - odległości środków ciężkości pól momentów od odpowiednich podpór
a także zapis w takiej postaci jak poniżej
\[ \mathrm{x}_{\mathrm{k}-1} \cdot \mathrm{l}_{\mathrm{k}^{\prime}}+2 \cdot \mathrm{x}_{\mathrm{k}} \cdot\left(\mathrm{l}_{\mathrm{k}^{\prime}}+\mathrm{l}_{\mathrm{k}+1^{\prime}}\right)+\mathrm{x}_{\mathrm{k}+1^{-1}} \mathrm{l}_{\mathrm{k}+1^{\prime}}=\mathrm{N}_{\mathrm{k}} \mathrm{P} \]Legenda:
- \( \mathrm{x}_{\mathrm{k}-1}, \mathrm{x}_{\mathrm{k}}, \mathrm{x}_{\mathrm{k}+1^{-1}} \) – momenty zginające w kolejnych podporach (poprzednia, bieżąca, następna).
- \( \mathrm{l}_{\mathrm{k}'} \) – sprowadzona (porównawcza) długość przęsła pomiędzy podporami \(k-1\) i \(k\).
- \( \mathrm{l}_{\mathrm{k}+1'} \) – sprowadzona (porównawcza) długość przęsła pomiędzy podporami \(k\) i \(k+1\).
- \( \mathrm{N}_{\mathrm{k}} \) = \(-6 \mathrm{EI} \cdot\left(\varphi_{k \mathrm{~L}}+\varphi_{k \mathrm{P}}\right)\) gdzie: \( I_C \) - porównawczy moment bezwładności (moment bezwładności jednego z przęseł wybieramy jako porównawczy)
Przykład 1
Rozwiązać zadaną belkę metodą trzech momentów. Narysować ostateczne wykresy momentów gnących i sił tnących.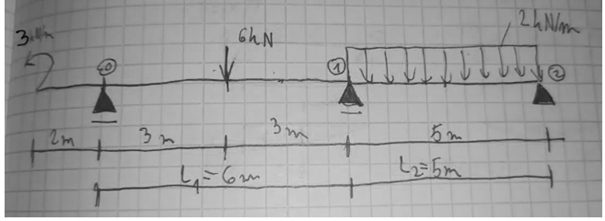
Rys1. Temat zadania
Pokażemy tutaj rozwiązanie stosując oznaczenia z ostatniego wariantu wzoru jaki podaliśmy we wstępie.
Redukcja części wyznaczalnej, określenie momentów brzegowych
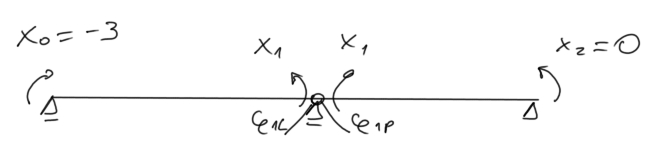
Rys2. Określenie momentów brzegowych
Jeżeli \( I = \text{const} \), to \( l_k' = l_k \)
Dane:
- \( l_1 = l_1' = 6\,\text{m} \)
- \( l_2 = l_2' = 5\,\text{m} \)
Równanie trzech momentów:
\[ x_{k-1} \cdot l_k' + 2 \cdot x_k \cdot (l_k' + l_{k+1}') + x_{k+1} \cdot l_{k+1}' = N_k P \]
\[ x_0 \cdot l_1' + 2 \cdot x_1 \cdot (l_1' + l_2') + x_2 \cdot l_2' = N_1 P \]
\[ -3 \cdot 6 + 2 \cdot x_1 \cdot (6 + 5) + 0 \cdot 5 = N_1 P \]
\[ 22 \cdot x_1 = N_1 P + 18 \]
Obliczenie prawej strony równania trzech momentów
podejście z całkowaniem graficznym figur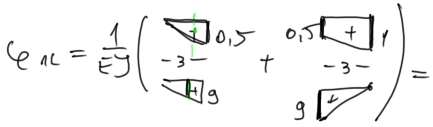
\[ = \frac{1}{EI} \left( 3 \cdot 0{,}5 \cdot \frac{1}{2} \cdot \frac{2}{3} \cdot 9 + \frac{3}{6} \left( 0{,}5 \cdot 9 + 1\cdot 0 + 4\cdot 4,5 \cdot 0{,}75 \right) \right) = \frac{13{,}5}{EI} \]
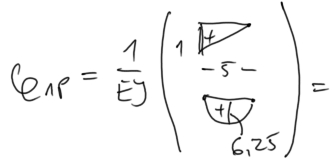
\[ = \frac{1}{EI} \left( \frac{5}{6} \left( 1\cdot 0 + 0 \cdot 0 + 4 \cdot 0{,}5 \cdot 6{,}25 \right) \right) = \frac{125}{12EI} \]
Do całkowania powyższych przykładów użyto wzoru Simpsona
\[ N_{1P} = -6EI \cdot (\varphi_{1L} + \varphi_{1P}) = -6EI \cdot \left( \frac{13{,}5}{EI} + \frac{125}{12EI} \right) \]
\[ N_{1P} = -143{,}5 \]
Równanie 3M:
\[ 22x_1 = N_{1P} + 18 = -143{,}5 + 18 \]
\[ x_1 = -5{,}7\ \text{kNm} \]
\[ M_{\text{ost}} = M_1 \cdot x_1 + M_P \]
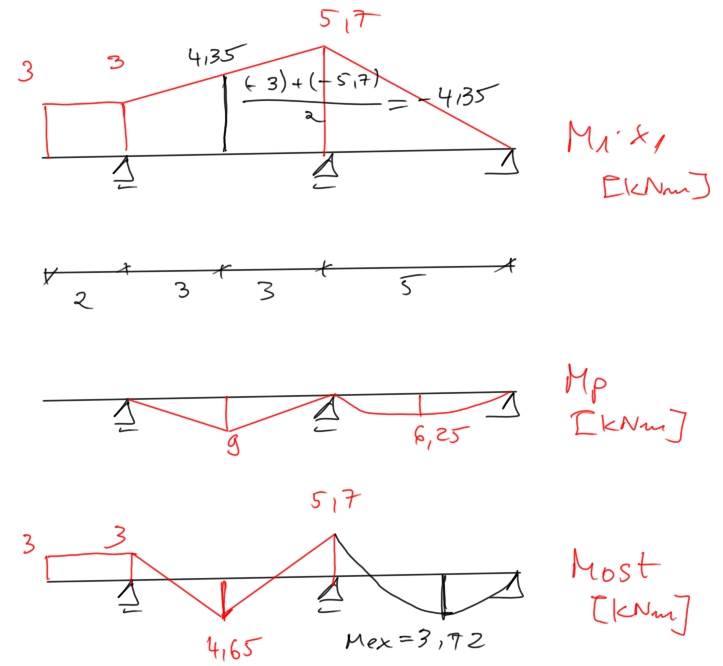
Wyznaczenie ostatecznych reakcji i sił tnących
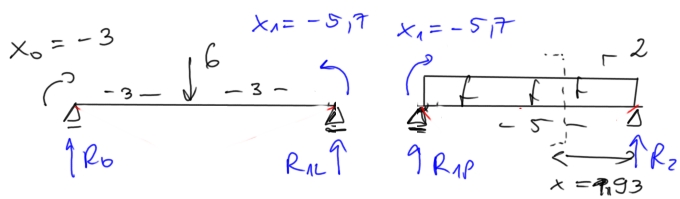
|
\[ \sum M_0 = 0 \quad \curvearrowright \] \[ -3 + 6 \cdot 3 + 5{,}7 - R_{1L} \cdot 6 = 0 \] \[ R_{1L} = 3{,}45\ \text{kN} \] \[ \sum Y = 0 \] \[ R_0 - 6 + R_{1L} = 0 \] \[ R_0 = 2{,}55\ \text{kN} \] |
\[ \sum M_1 = 0 \] \[ -5{,}7 + 2{,}5 \cdot 2{,}5 - R_2 \cdot 5 = 0 \] \[ R_2 = 3{,}86\ \text{kN} \] \[ \sum Y = 0 \] \[ R_{1P} - 2{,}5 + R_2 = 0 \] \[ R_{1P} = 6{,}14\ \text{kN} \] |
sprawdzenie
\[ R_1=R_{1L}+R_{1P}=9,59 \ kN \\ \sum y=0 \ \ R_0+R_1+R_2-6-2\cdot 5=0 \\ 0=0 \\ \] Ostateczny wykres sił tnących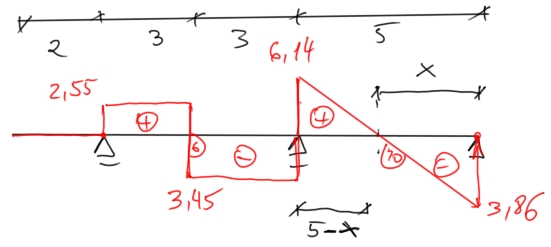
Obliczenie ekstremum na wykresie momentów:
\[\frac{3,86}{x} = \frac{6,14}{5-x}\]
\[6,14x = 3,86 \cdot (5-x)\]
\[6,14x = 19,3 - 3,86x\]
\[10x = 19,3 \quad (:10)\]
\[x = 1,93\text{m}\]
\[M_{ex} = R_z \cdot x - 2 \cdot x \cdot \frac{x}{2} = 3,72\text{ kNm}\]
Przykład 2
Zobaczmy częściowo rozwiązany kolejny przykład - celem pokazania jak traktować podporę typu utwierdzenie przy metodzie trzech momentów, a także jak uwzględnić różne sztywności przęseł.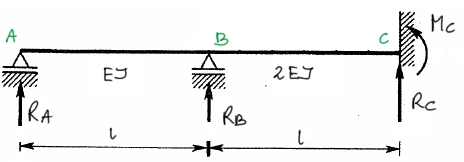
Rys3. Temat zadania 2
Wykorzystując równanie trzech momentów, sporządzić wykresy sił tnących i momentów gnących dla belki przedstawionej na rys3.
Dane: \( q,\ l,\ c = \frac{2EI}{EI} = 2 \)
Rozwiązanie:
Belka jest dwukrotnie statycznie niewyznaczalna. Brakujące dwa równania uzyskujemy stosując metodę trzech momentów dla przęseł 1 i 2 oraz 2 i 3
(przęsło 3 o długości zerowej!).
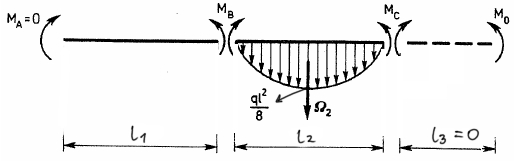
Rys4. Opisanie długości przęseł, zaznaczenie momentów na końcach elementów.
\[ cM_A l_1 + 2M_B(c l_1 + l_2) + M_C l_2 = -6c \cdot \frac{\Omega_1 a_1}{l_1} - 6 \cdot \frac{\Omega_2 b_2}{l_2} \]
\[ M_B l_2 + 2M_C(l_2 + l_3) + M_0 l_3 = -6 \cdot \frac{\Omega_2 a_2}{l_2} - 6 \cdot \frac{\Omega_3 b_3}{l_3} \]
Do równań należy wstawić:
- \( l_1 = l_2 = l \),
- \( l_3 = 0 \),
- \( c = 2 \),
- \( M_A = 0 \),
- \( \Omega_1 = 0 \),
- \( \Omega_2 = \frac{2}{3} \cdot \frac{1}{8} q l^2 \cdot l = \frac{1}{12} q l^3 \),
- \( \Omega_3 = 0 \),
- \( a_2 = \frac{1}{2} l \)
Po przekształceniu równań trzech momentów otrzymujemy układ równań:
\[ \begin{cases} 6M_B + M_C = -\frac{1}{4} ql^2 \\ M_B + 2M_C = -\frac{1}{4} ql^2 \end{cases} \]
Rozwiązując ten układ równań, otrzymujemy wartości momentów w podporach:
\[ M_B = -\frac{1}{44} ql^2, \quad M_C = -\frac{5}{44} ql^2 \]
Wyznaczenie reakcji podporowych
Aby obliczyć reakcje podporowe, rozpatrujemy równowagę poszczególnych przęseł. Z równania momentów względem punktu B (dla przęsła AB) otrzymujemy:
\[ R_A = \frac{M_B}{l} = -\frac{1}{44} ql \]
Równoważąc siły działające na przęśle AB, otrzymujemy wartość siły reakcji od strony przęsła:
\[ R'_B = -R_A = \frac{1}{44} ql \]
Dla przęsła BC, korzystając z równania równowagi momentów względem punktu B:
\[ R_C = \frac{M_B - M_C}{l} + \frac{ql}{2} = \frac{13}{22} ql \]
Następnie wyznaczamy siłę przekazywaną z prawej strony przęsła do punktu B:
\[ R''_B = ql - R_C = \frac{9}{22} ql \]
Całkowita reakcja w podporze B to suma reakcji z lewej i prawej strony:
\[ R_B = R'_B + R''_B = \frac{1}{44} ql + \frac{9}{22} ql = \frac{19}{44} ql \]
Dysponując obliczonymi momentami i reakcjami, możemy teraz sporządzić wykresy sił tnących i momentów gnących dla całej belki.
Źródło: zadanie 10.15 (str. 379) z:
M. Banasiak, K. Grossman, M. Trombski, „Zbiór zadań z wytrzymałości materiałów”, Wydawnictwo Naukowe PWN, Warszawa 2012.

