Żeby uzyskać dostęp do tego zadania musisz wykupić abonament ->
Sklep
Jeżeli masz już abonament a nadal widzisz ten komunikat upewnij się czy jesteś zalogowany
Przykład 14
Problem brzegowy:
\[ \begin{cases} y''(x) = -4, \\ y'(-2) = 1{,}5, \\ y(2) = -1, \end{cases} \quad x \in [-2, 2] \]
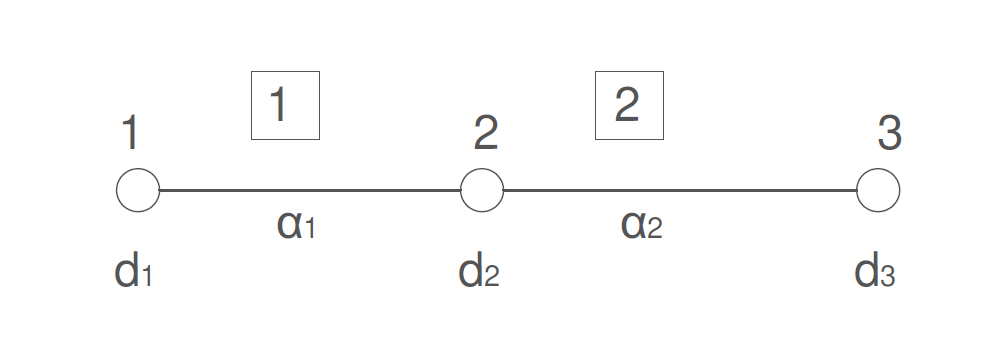
Rozwiązano MES dyskretyzując dziedzinę dwoma elementami skończonymi z kwadratowymi hierarchicznymi funkcjami kształtu. Zbudowano układ równań MES, uwzględniono warunki brzegowe, a następnie go rozwiązano. Rozwiązaniem tego układu równań są następujące wielkości: \[ d_1 = 25,\quad d_2 = 20,\quad \alpha_1 = -2,\quad \alpha_2 = -2,\quad y'(2) = 0 \] Zapisać rozwiązanie MES \( y_h \). Wyznaczyć estymator błędu dla obu elementów przyjmując, że rozwiązanie ścisłe wynosi \[ y_{\text{exact}} = 20 - \frac{13}{2}x - 2x^2. \]
UWAGA: Wartości brakujących stopni swobody należy wywnioskować na podstawie warunków brzegowych.