Solution
Classic Version
We encourage you to watch the solution to this example (as well as the others) on our YouTube channel. I explain how to solve this task from start to finish in the video. Watching this video will also help you understand the other examples on our website.
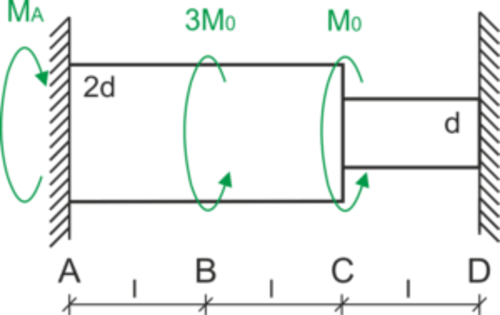
Geometric condition - the total angle of twist is equal to 0:
\begin{aligned}\\ &\varphi_c =0\\ &\varphi=\frac{M_S\cdot l}{G\cdot I}\\ \\ &M_{AB}=M_A\\ &M_{BC}=M_A-3M_0\\ &M_{CD}=M_A-4M_0\\ \\ &I=\frac{\pi \cdot d^4}{32}\\ \\ &I_{AB}=I_{BC}=\frac{\pi \cdot (2d)^4}{32}=\frac{\pi \cdot d^4}{2}\\ &I_{CD}=\frac{\pi \cdot d^4}{32}\\ \end{aligned}In order to simplify further calculations, we determine the ratio of the moments of inertia:
\begin{aligned}\\ &\frac{I_{AB}}{I_{CD}}=\frac{\pi d^4}{2}\cdot \frac{32}{\pi d^4}=16\ \Rightarrow I_{AB}=16I_{BC}\\ \\ &\varphi_c=\varphi_{AB}+\varphi_{BC}+\varphi_{CD}=0\\ &\varphi_c=\frac{M_A\cdot l}{G\cdot 16I_{CD}}+\frac{(M_A-3M_0)\cdot l}{G\cdot 16I_{CD}}+\frac{(M_A-4M_0)\cdot l}{G\cdot I_{CD}}=0\ |\cdot \frac{GI_{BC}}{l}\\ &\frac{1}{16}M_A+\frac{1}{16}M_A-\frac{3}{16}M_0+M_A-4M_0=0\\ &\frac{18}{16}M_A=\frac{67}{16}M_0\\ &M_A=\frac{67}{18}M_0=3.72M_0=3.72\ kNm\\ \end{aligned}Shear Stresses
\begin{aligned}\\ &\tau =\frac{M_S}{W_S}\\ &W_S=\frac{\pi \cdot d^3}{16}\\ \\ &W_{S_{AB}}=W_{S_{BC}}=\frac{\pi \cdot 0.1^3}{16}=1.96\cdot 10^{-4}\ m^3\\ &W_{S_{CD}}=\frac{\pi \cdot 0.05^3}{16}=2.45\cdot 10^{-5}\ m^3\\ \\ &\tau_{AB}=\frac{M_{AB}}{W_{S_{AB}}}=\frac{3.72\cdot 10^3}{1.96\cdot 10^{-4}}=18.98\ MPa\\ \\ &\tau_{BC}=\frac{0.72\cdot 10^3}{2.45\cdot 10^{-5}}=3.67\ MPa\\ &\tau_{CD}=\frac{-0.28\cdot 10^3}{2.45\cdot 10^{-5}}=-11.43\ MPa\\ \end{aligned}Angle of Twist at Section C
The angle of twist between two sections that are x units apart is given by:
\begin{aligned} &\varphi =\int\limits_{0}^{x} \frac{M_s(x)}{GI_0}dx\\ \end{aligned} \begin{aligned}\\ &I_{AB}=I_{BC}=\frac{\pi \cdot 0.1^4}{32}=9.82\cdot 10^{-6}\ m^4\\ &I_{CD}=\frac{\pi \cdot 0.05^4}{32}=6.14\cdot 10^{-7}\ m^4\\ \\ &\varphi_C=\varphi_{AB}+\varphi_{BC}\\ &\varphi_C=\int\limits_{0}^{1} \frac{3.72\cdot 10^3}{80\cdot 10^9\cdot 9.82\cdot 10^{-6}}dx+\int\limits_{0}^{1} \frac{0.72\cdot 10^3}{80\cdot 10^9\cdot 9.82\cdot 10^{-6}}dx=4.74\cdot 10^{-3}+9.16\cdot 10^{-4}=5.66\cdot 10^{-3}\ rad\\ &5.66\cdot 10^{-3}\ rad=5.66\cdot 10^{-3}\cdot \frac{180}{\pi} [^o] =0.32^o\\ \end{aligned}Graphs
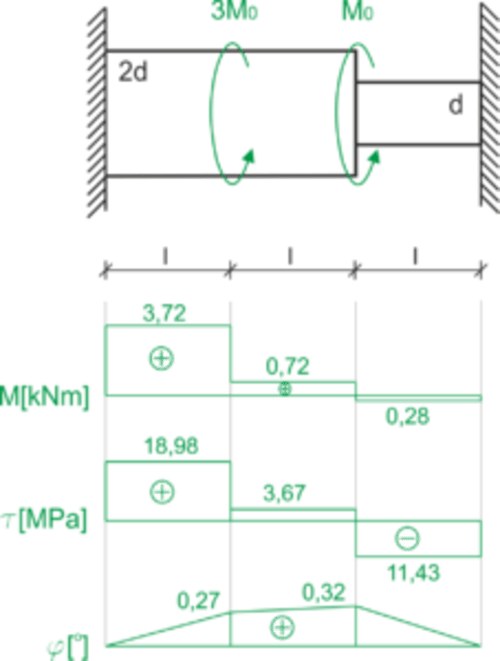
Source:
Niezgodziński Michał E., Tadeusz Niezgodziński, Zadania z wytrzymałości materiałów, WNT, Warszawa 2002, Przykład 5.10 s. 69
