Solution
We do encourage you to watch the solution of this example (and the others) on our YouTube channel. There is explained there how this task should be solved step-by-step. Watching this video will also help you understand the other examples on our website.
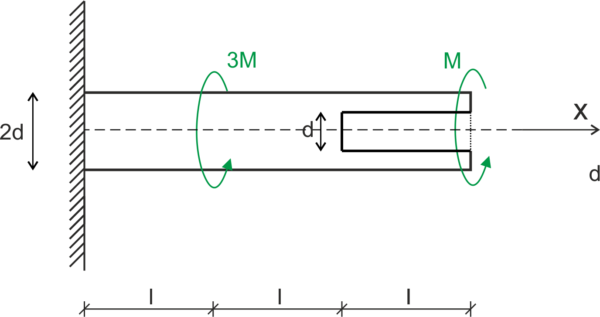
\begin{aligned} &\sum M=0 \\ &M_{A}-3 M-M=0 \\ &M_{A}=4 M \\ &M_{A B}=4 M \\ &M_{B C}=M \\ &M_{C D}=M \end{aligned}The carrying capacity limit state:
\begin{aligned} &\tau_{\max } \geq k_{s}\\ &\tau=\frac{M_{S}}{W_{S}}\\ &W_{A B}=W_{B C}=\frac{\pi \cdot(2 d)^{3}}{16}=\frac{\pi \cdot d^{3}}{2}\\ &W_{C D}=\frac{\pi \cdot\left((2 d)^{4}-d^{4}\right)}{16 \cdot(2 d)}=\frac{15 \cdot \pi \cdot d^{3}}{32}\\ &\tau_{A B}=\frac{4 M}{\frac{\pi \cdot d^{3}}{2}}=\frac{8 M}{\pi \cdot d^{3}}\\ &\tau_{A B}=\frac{M}{\frac{15 \cdot \pi \cdot d^{3}}{32}}=\frac{32 M}{15 \cdot \pi \cdot d^{3}}\\ &\tau_{\max }=\tau_{A B}\\ &\frac{8 M}{\pi \cdot d^{3}} \leq k_{s} \Rightarrow M \leq \frac{k_{s} \cdot \pi \cdot d^{3}}{8}\\ &\varphi=\frac{M_{S} \cdot l}{G \cdot I}\\ &I_{A B}=\frac{\pi \cdot(2 d)^{4}}{32}=\frac{\pi \cdot d^{4}}{2}\\ &I_{C D}=\frac{\pi \cdot\left((2 d)^{4}-d^{4}\right)}{32}=\frac{15 \pi \cdot d^{4}}{32}\\ &\varphi_{A B}=\frac{4 M \cdot l}{G \cdot \frac{\pi d^{4}}{2}}=\frac{8 M \cdot l}{G \cdot \pi d^{4}}\\ &\varphi_{B C}=\frac{M \cdot l}{G \cdot \frac{\pi d^{4}}{2}}=\frac{2 M \cdot l}{G \cdot \pi d^{4}}\\ &\varphi_{C D}=\frac{M \cdot l}{G \cdot \frac{15 \pi d^{4}}{32}}=\frac{32 M \cdot l}{15 G \cdot \pi d^{4}}\\ &\varphi_{C}=\varphi_{A B}+\varphi_{B C}+\varphi_{C D}\\ &\varphi_{C}=\frac{8 M \cdot l}{G \cdot \pi d^{4}}+\frac{2 M \cdot l}{G \cdot \pi d^{4}}+\frac{32 M \cdot l}{15 G \cdot \pi d^{4}}\\ &\varphi_{C}=\frac{182 M l}{15 G \pi d^{4}} \end{aligned}Source (topic od the task): Niezgodziński Michał E., Tadeusz Niezgodziński, Zadania z wytrzymałości materiałów, WNT, Warszawa 2002, Przykład 5.6 s. 68
If you have any questions, comments, or think you have found a mistake in this solution, please send us a message at kontakt@edupanda.pl.