Solution
 \begin{aligned}
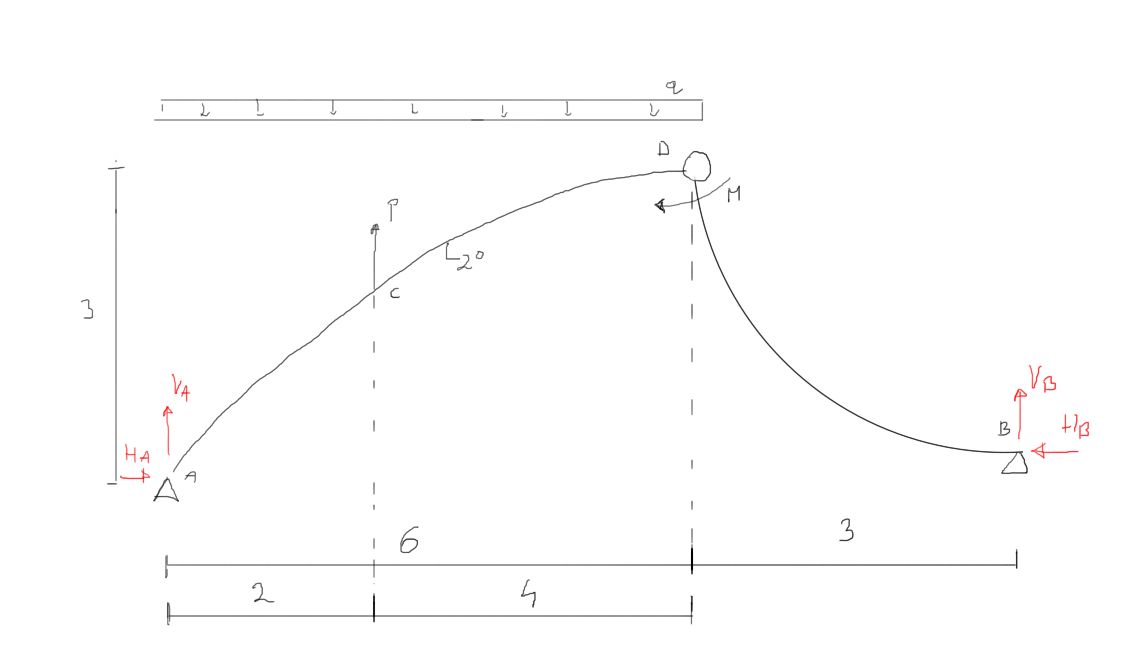
&\Sigma M_{A}=0 \\
&-P \cdot 2+q \cdot 6 \cdot 3+M-V_{B} \cdot 9=0 \\
&V_{B}:=\frac{-P \cdot 2+q \cdot 6 \cdot 3+M}{9}=84.444 k N \\
&\Sigma Y=0 \\
&V_{A}+V_{B}+P-6 q=0 \\
&V_{A}:=-\left(V_{B}+P-6 q\right)=125.556 k N \\
&\Sigma_{B}:=\frac{-1}{3}\left(M-V_{B} \cdot 3\right)=51.111 k N
\end{aligned}
$$
\begin{aligned}
&\Sigma X=0 \\
&H_{A}:=H_{B}=51.111 \quad k N
\end{aligned}
$$
Shape of a parabolic arc axis:
$$
\begin{aligned}
&y=\frac{4 f}{l^{2}} x \cdot(l-x) \\
&\frac{d y}{d x}=\tan (\varphi)=\frac{4 f}{l^{2}}(l-2 x)
\end{aligned}
$$
$$
\begin{aligned}
&\sin (\varphi)=\frac{\tan (\varphi)}{\sqrt{1+\tan (\varphi)^{2}}} \\
&\cos (\varphi)=\frac{1}{\sqrt{1+\tan (\varphi)^{2}}}
\end{aligned}
$$
\begin{aligned}
&f:=3 \quad l:=12 \\
&y^{\prime}=\tan \varphi=\frac{4 f}{l^{2}}(l-2 x)=1-\frac{x}{6} \\
&y=\frac{4 f}{l^{2}} x \cdot(l-x)=-\frac{x^{2}}{12}+x \\
&y(2)=-\frac{2^{2}}{12}+2=\frac{5}{3}
\end{aligned}
For a parabolic arc:
\begin{aligned}
&\Sigma M_{A}=0 \\
&-P \cdot 2+q \cdot 6 \cdot 3+M-V_{B} \cdot 9=0 \\
&V_{B}:=\frac{-P \cdot 2+q \cdot 6 \cdot 3+M}{9}=84.444 k N \\
&\Sigma Y=0 \\
&V_{A}+V_{B}+P-6 q=0 \\
&V_{A}:=-\left(V_{B}+P-6 q\right)=125.556 k N \\
&\Sigma_{B}:=\frac{-1}{3}\left(M-V_{B} \cdot 3\right)=51.111 k N
\end{aligned}
$$
\begin{aligned}
&\Sigma X=0 \\
&H_{A}:=H_{B}=51.111 \quad k N
\end{aligned}
$$
Shape of a parabolic arc axis:
$$
\begin{aligned}
&y=\frac{4 f}{l^{2}} x \cdot(l-x) \\
&\frac{d y}{d x}=\tan (\varphi)=\frac{4 f}{l^{2}}(l-2 x)
\end{aligned}
$$
$$
\begin{aligned}
&\sin (\varphi)=\frac{\tan (\varphi)}{\sqrt{1+\tan (\varphi)^{2}}} \\
&\cos (\varphi)=\frac{1}{\sqrt{1+\tan (\varphi)^{2}}}
\end{aligned}
$$
\begin{aligned}
&f:=3 \quad l:=12 \\
&y^{\prime}=\tan \varphi=\frac{4 f}{l^{2}}(l-2 x)=1-\frac{x}{6} \\
&y=\frac{4 f}{l^{2}} x \cdot(l-x)=-\frac{x^{2}}{12}+x \\
&y(2)=-\frac{2^{2}}{12}+2=\frac{5}{3}
\end{aligned}
For a parabolic arc:
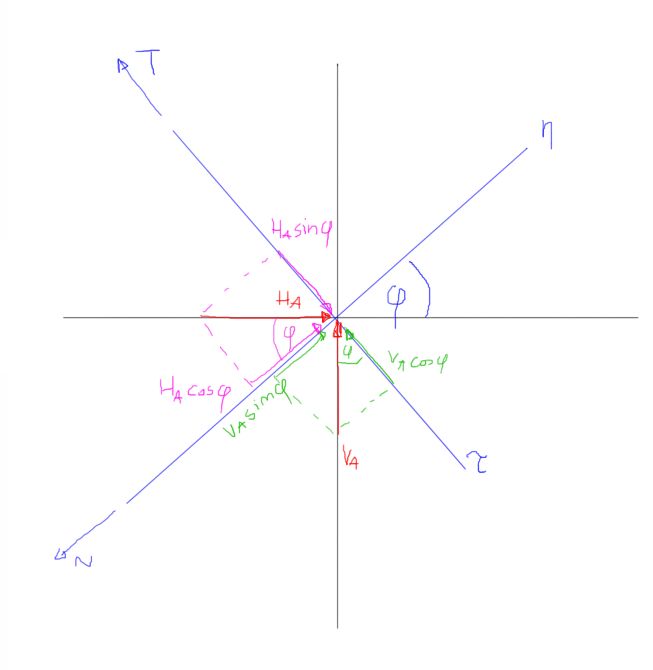 $$
\begin{aligned}
&N=-V_{A} \cdot \sin (\varphi)-H_{A} \cdot \cos (\varphi) \\
&T=V_{A} \cdot \cos (\varphi)-H_{A} \cdot \sin (\varphi)
\end{aligned}
$$
$$
\begin{aligned}
&N=-V_{A} \cdot \sin (\varphi)-H_{A} \cdot \cos (\varphi) \\
&T=V_{A} \cdot \cos (\varphi)-H_{A} \cdot \sin (\varphi)
\end{aligned}
$$
Section AC
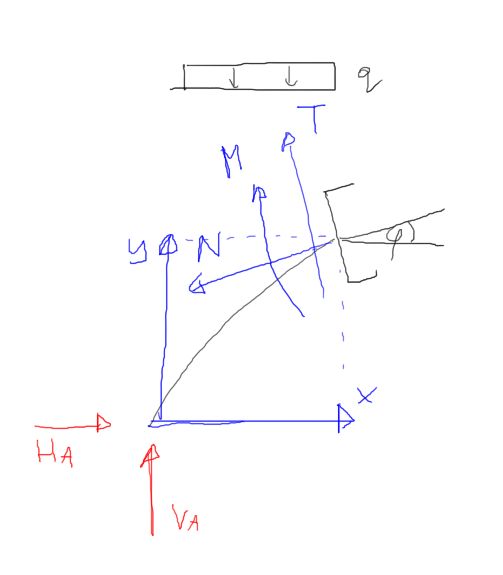 $$
\begin{aligned}
&x(0 ; 2) \\
&T(x)=125.556 \cdot \cos \varphi-51.111 \cdot \sin \varphi-40 x \cdot \cos (\varphi) \\
&N(x)=-125.556 \cdot \sin \varphi-51.111 \cdot \cos \varphi+40 x \cdot \sin (\varphi) \\
&M(x)=125.556 x-51.111 y-40 \cdot x \cdot \frac{x}{2} \\
&M(x)=125.556 x-51.111\left(x-\frac{x^{2}}{12}\right)-40 \cdot x \cdot \frac{x}{2}
\end{aligned}
$$
$$
\begin{aligned}
&x(0 ; 2) \\
&T(x)=125.556 \cdot \cos \varphi-51.111 \cdot \sin \varphi-40 x \cdot \cos (\varphi) \\
&N(x)=-125.556 \cdot \sin \varphi-51.111 \cdot \cos \varphi+40 x \cdot \sin (\varphi) \\
&M(x)=125.556 x-51.111 y-40 \cdot x \cdot \frac{x}{2} \\
&M(x)=125.556 x-51.111\left(x-\frac{x^{2}}{12}\right)-40 \cdot x \cdot \frac{x}{2}
\end{aligned}
$$
If you have any questions, comments, or think you have found a mistake in this solution, please send us a message at kontakt@edupanda.pl.
