Solution
The figure has one axis of symmetry, so we take one of the axes of the coordinate system on it. We can choose the second axis arbitrarily, for example along the bottom edge as shown below.
We are looking for the vertical coordinate of the center of gravity "yc". We calculate it as the ratio of the static moment of inertia to the total cross-sectional area. It is helpful to write down the "y-coordinate" of the center of gravity of each individual rectangular figure (y1 and y2) and their area (A1 and A2) as auxiliary values.
Calculation of the position of the center of gravity
\begin{aligned} &y_1=3.5a & A_1=3a^2\\ &y_2=1.5a & A_2=3a^2\\ &y_c=\frac{y_1A_1+y_2A_2}{A_1+A_2}=\frac{3.5a\cdot 3a^2+1.5a\cdot 3a^2}{3a^2+3a^2}=2.5a\\ \end{aligned}We mark the calculated center of gravity on the diagram, and the horizontal axis transferred to the center of gravity is the central principal axis.
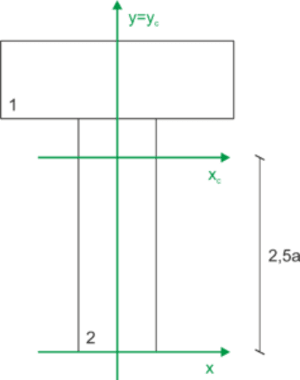
Calculation of the moment of inertia with respect to the central principal axes
To calculate the moment of inertia with respect to the horizontal axis, we need to use the Steiner's theorem, which is not necessary for the vertical axis.
\begin{aligned} &I_{XC}=I_{X1}+A_1(y_1-y_C)^2+I_{X2}+A_2(y_2-y_C)^2\\ &I_{XC}=\frac{3a\cdot a^3}{12}+3a^2(3.5a-2.5a)^2+\frac{a\cdot(3a)^3}{12}+3a^2(1.5a-2.5a)^2=8.5a^4\\ &I_{YC}=I_{Y1}+I_{Y2}\\ &I_{YC}=\frac{(3a)^3\cdot a}{12}+\frac{a^3\cdot 3a}{12}=2.5a^4\\ \end{aligned}