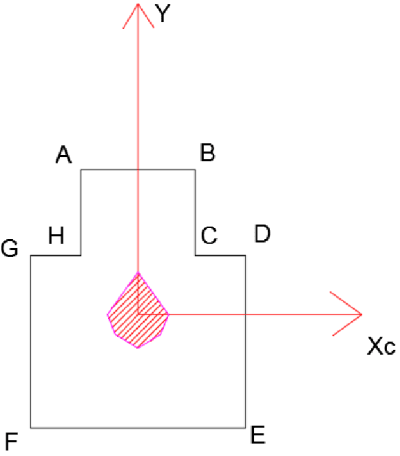
Solution
Geometric characteristics, central moments of inertia
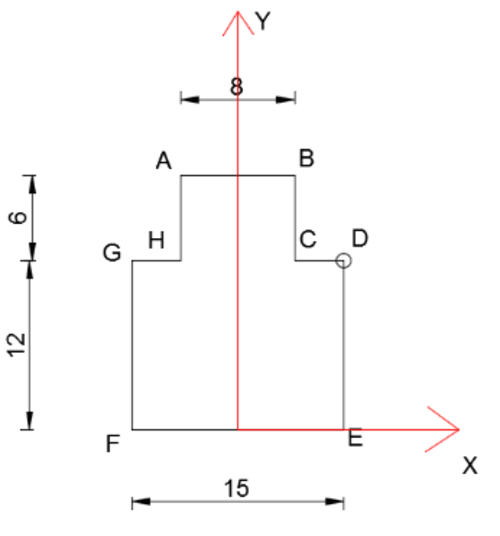
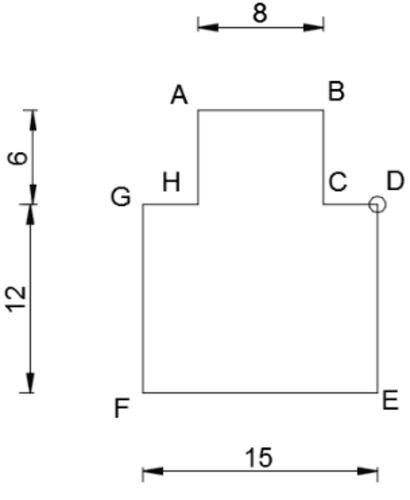
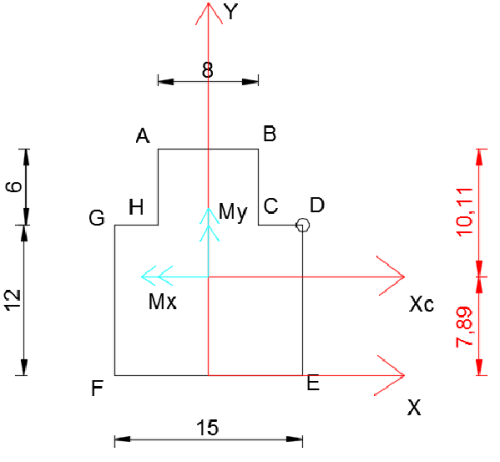
Figure 1 - larger rectangle, Figure 2 - smaller rectangle
\begin{aligned} a&A_1 =180 cm^2\\ &A_2 =48 cm^2\\ &A=A_1 +A_2=228 cm^2\\ &y_1 =6 cm\\ &y_2 =15 cm\\ &y_c=\frac{y_1 ⋅A_1+ y_2 ⋅A_2}{A_1 +A_2}=7.89 cm\\ \end{aligned}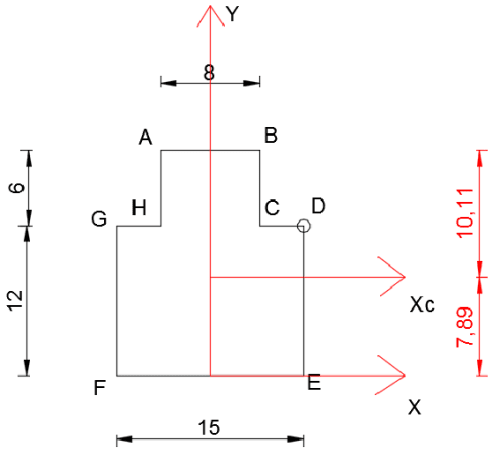 \begin{aligned} &I_{xc}=\frac{15\cdot 12^3}{12}+A_1\cdot (y_1-y_c)^2+\frac{8\cdot 6^3}{12}+A_2\cdot (y_2-y_c)^2=5373.47 cm^4\\ &I_{yc}=\frac{12\cdot 15^3}{12}+\frac{6\cdot 8^3}{12}=3631 cm^4\\ \end{aligned}
\begin{aligned} &I_{xc}=\frac{15\cdot 12^3}{12}+A_1\cdot (y_1-y_c)^2+\frac{8\cdot 6^3}{12}+A_2\cdot (y_2-y_c)^2=5373.47 cm^4\\ &I_{yc}=\frac{12\cdot 15^3}{12}+\frac{6\cdot 8^3}{12}=3631 cm^4\\ \end{aligned}
The force at point D directed "behind the page" (compressive) creates moments Mx and My with the directions shown in the image below (right-hand rule).
Determination of the neutral axis equation
\begin{aligned} &N=-60 kN\\ &M_y=-|N|\cdot 0.075=-4.5 kNm\\ &M_x=-|N|\cdot |(0.12-0.0789)|=-2.466 kNm\\ &\sigma_x=\frac{-60\cdot 10^3}{228\cdot 10^{-4}}-\frac{2.466\cdot 10^3}{5373.37\cdot 10^{-8}}y-\frac{4.5\cdot 10^3}{3631\cdot 10^{-8}}x=0\\ &y=-2.7x-5.7\\ \end{aligned}Two arbitrary points define a straight line (neutral axis).
\begin{aligned} &x=1, y=-8.4\\ &x=-1, y=-3\\ \end{aligned}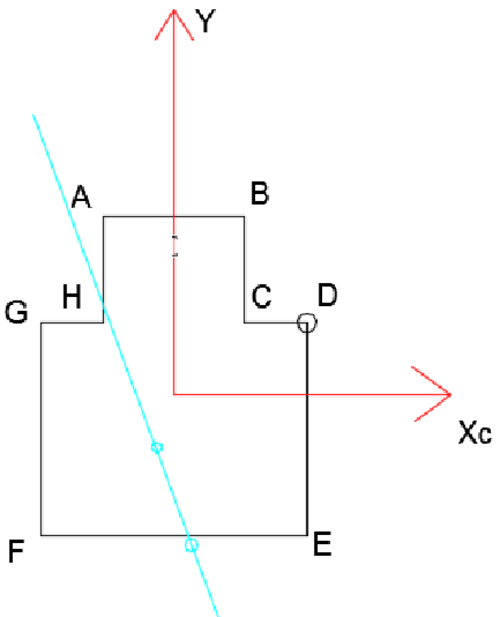
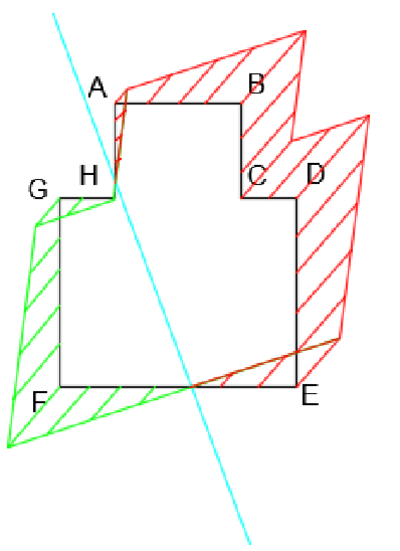
Stresses at characteristic points
\(\sigma=\frac{-60\cdot 10^3}{0.023}-\frac{2.466\cdot 10^3}{5373.37\cdot 10^{-8}}y-\frac{4.5\cdot 10^3}{3631\cdot 10^{-8}}x\)Point A (x=-4 cm, y=10.11 cm)
\(\sigma=-2.29 MPa\)Point B (x=4 cm, y=10.11 cm)
\(\sigma=-12.21 MPa\)Point C (x=4 cm, y=(12-7.89) cm)
\(\sigma=-9.45 MPa\)Point D (x=7.5 cm, y=(12-7.89) cm)
\(\sigma=-13.79 MPa\)Point E (x=7.5 cm, y=-7.89 cm)
\(\sigma=-8.28 MPa\)Point F (x=-7.5 cm, y=-7.89 cm)
\(\sigma=10.31 MPa\)Point G (x=-7.5 cm, y=(12-7.89) cm)
\(\sigma=4.8 MPa\)Point H (x=-4 cm, y=(12-7.89) cm)
\(\sigma=0.46 MPa\)Stress block
Core of the section
We mark tangents to the section (in purple), and for each tangent we determine one corner point of the core of the section.
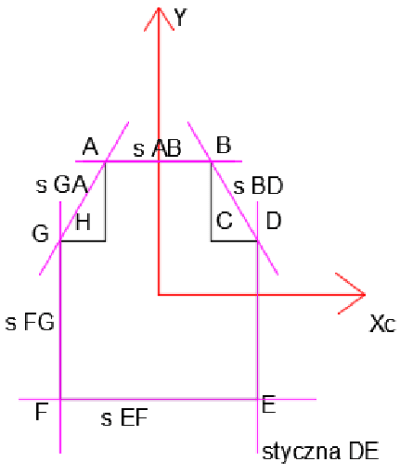 \begin{aligned} &i_x^2=\frac{I_{xc}}{A}=23.57 cm^2\\ &i_y^2=\frac{I_{yc}}{A}=15.93 cm^2\\ \end{aligned}
\begin{aligned} &i_x^2=\frac{I_{xc}}{A}=23.57 cm^2\\ &i_y^2=\frac{I_{yc}}{A}=15.93 cm^2\\ \end{aligned}
We will use the equation of a line passing through two points:
\begin{aligned} &y-y_1=\frac{y_2-y_1}{x_2-x_1}\cdot (x-x_1)\\ \end{aligned}Neutral axis D-E
\begin{aligned} &a_y=\infty\\ &a_x=7.5 cm\\ &y=-\frac{i_x}{a_y}=0 cm\\ &x=-\frac{i_y}{a_x}=-2.12 cm\\ \end{aligned}Neutral axis E-F
\begin{aligned} &a_y=-7.89 cm\\ &a_x=\infty\\ &y=-\frac{i_x}{a_y}=2.99 cm\\ &x=-\frac{i_y}{a_x}=0 cm\\ \end{aligned}Neutral axis F-G
\begin{aligned} &a_y=\infty\\ &a_x=-7.5 cm\\ &y=-\frac{i_x}{a_y}=0 cm\\ &x=-\frac{i_y}{a_x}=2.12 cm\\ \end{aligned}Neutral axis G-A
\begin{aligned} &y-y_G=\frac{y_A-y_G}{x_A-x_G}\cdot (x-x_G)\\ &x_G=-7.5 cm, y_G=4.11 cm\\ &x_A=-4 cm, y_A=10.11 cm\\ &y=1.71x+16.96\\ &a_y=16.96 cm\\ &a_x=-9.89 cm\\ &y=-\frac{i_x}{a_y}=-1.39 cm\\ &x=-\frac{i_y}{a_x}=1.61 cm\\ \end{aligned}Neutral axis A-B
\begin{aligned} &a_y=10.11 cm\\ &a_x=\infty\\ &y=-\frac{i_x}{a_y}=-2.33 cm\\ &x=-\frac{i_y}{a_x}=0 cm\\ \end{aligned}Neutral axis B-D
\begin{aligned} &x_B=4 cm, y_B=10.11 cm\\ &x_D=7.5 cm, y_D=4.11 cm\\ &y=-1.71x+16.96\\ &a_y=16.96 cm\\ &a_x=9.89 cm\\ &y=-\frac{i_x}{a_y}=-1.39 cm\\ &x=-\frac{i_y}{a_x}=-1.61 cm\\ \end{aligned}Core of the section