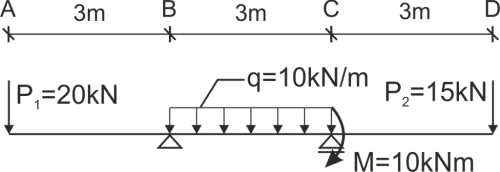
Solution
Attention - understanding this example may be helpful by reading the theoretical introduction and watching the video course below:
Classical solution
We calculate the support reactions
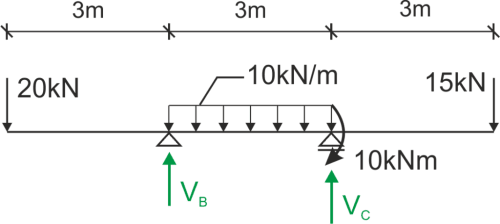 \begin{aligned} &\sum{M_B}=0 -20\cdot 3+30\cdot 1.5+10+15\cdot 6-R_C\cdot 3=0 R_A=28.33kN\\ &\sum{M_C}=0 -20\cdot 6+R_B\cdot 3-30\cdot 1.5+10+15\cdot 3=0 R_B=36.67kN\\ &\sum{P_iY}=0 -20+R_B-30+R_C-15=0 L=P\\ \end{aligned}
\begin{aligned} &\sum{M_B}=0 -20\cdot 3+30\cdot 1.5+10+15\cdot 6-R_C\cdot 3=0 R_A=28.33kN\\ &\sum{M_C}=0 -20\cdot 6+R_B\cdot 3-30\cdot 1.5+10+15\cdot 3=0 R_B=36.67kN\\ &\sum{P_iY}=0 -20+R_B-30+R_C-15=0 L=P\\ \end{aligned}
We write down the moment function on the left side.
The function can also be written on the right side. We encourage you to check this variant, calculate the desired displacement, and compare the results.
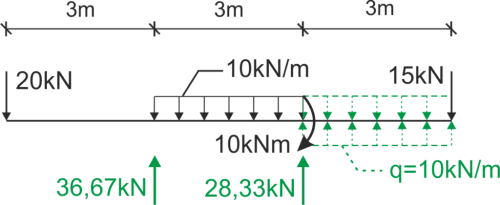 \begin{aligned} &M_g=-20x+R_B(x-3)-\frac{1}{2}q(x-3)^2+R_C(x-6)+10(x-6)^0+\frac{1}{2}q(x-6)^2\\ &EJW"=-M_g\\ &-M_g=20x-R_B(x-3)+5(x-3)^2- 28.33(x-6)-10(x-6)^0-5(x-6)^2\\ &EJW'=20\frac{x^2}{2}-36.67\frac{(x-3)^2}{2}+5\frac{(x-3)^3}{3}-28.33\frac{(x-6)^2}{2}-10(x-6)-5\frac{(x-6)^3}{3}+C\\ &EJW=20\frac{x^3}{6}-36.67\frac{(x-3)^3}{6}+5\frac{(x-3)^4}{12}-28.33\frac{(x-6)^3}{6}-10\frac{(x-6)^2}{2}-5\frac{(x-6)^4}{12}+Cx+D\\ \end{aligned}
\begin{aligned} &M_g=-20x+R_B(x-3)-\frac{1}{2}q(x-3)^2+R_C(x-6)+10(x-6)^0+\frac{1}{2}q(x-6)^2\\ &EJW"=-M_g\\ &-M_g=20x-R_B(x-3)+5(x-3)^2- 28.33(x-6)-10(x-6)^0-5(x-6)^2\\ &EJW'=20\frac{x^2}{2}-36.67\frac{(x-3)^2}{2}+5\frac{(x-3)^3}{3}-28.33\frac{(x-6)^2}{2}-10(x-6)-5\frac{(x-6)^3}{3}+C\\ &EJW=20\frac{x^3}{6}-36.67\frac{(x-3)^3}{6}+5\frac{(x-3)^4}{12}-28.33\frac{(x-6)^3}{6}-10\frac{(x-6)^2}{2}-5\frac{(x-6)^4}{12}+Cx+D\\ \end{aligned}
Boundary conditions
\begin{aligned} &W(3)=0 ---> 90+3C+D=0\\ &w(6)=0---> 588.735+6C+D=0\\ &C=-166,245\\ &D=408.735\\ \end{aligned}We calculate the deflection at point A.
\begin{aligned} &W_A=\frac{1}{EI}\cdot (408.735)\\ \end{aligned}
If you have any questions, comments, or think you have found a mistake in this solution, please send us a message at kontakt@edupanda.pl.