Solution
We encourage you to watch the solution of this example (as well as others) on our YouTube channel. I explain step by step how to solve this task in it. Watching this video will also help you understand the remaining examples on our website.
Reactions
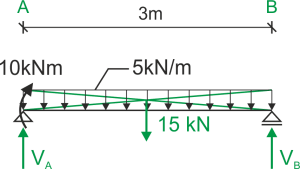 \begin{aligned}\\
&\sum{M_A}=0\\
&10+5\cdot 3\cdot \frac{3}{2}-3\cdot V_B=0 & V_B=10.83\ kN\\
&\sum{M_B}=0\\
&10+3\cdot V_A-3\cdot 5\cdot \frac{3}{2}=0 & V_A=4.17\ kN\\
&\sum{Y}=0 & V_A+V_C-5\cdot 3=0\\
\end{aligned}
\begin{aligned}\\
&\sum{M_A}=0\\
&10+5\cdot 3\cdot \frac{3}{2}-3\cdot V_B=0 & V_B=10.83\ kN\\
&\sum{M_B}=0\\
&10+3\cdot V_A-3\cdot 5\cdot \frac{3}{2}=0 & V_A=4.17\ kN\\
&\sum{Y}=0 & V_A+V_C-5\cdot 3=0\\
\end{aligned}
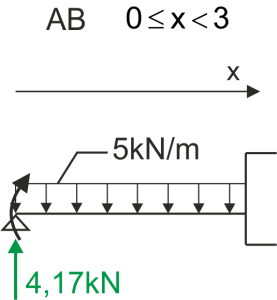 \begin{aligned}\\
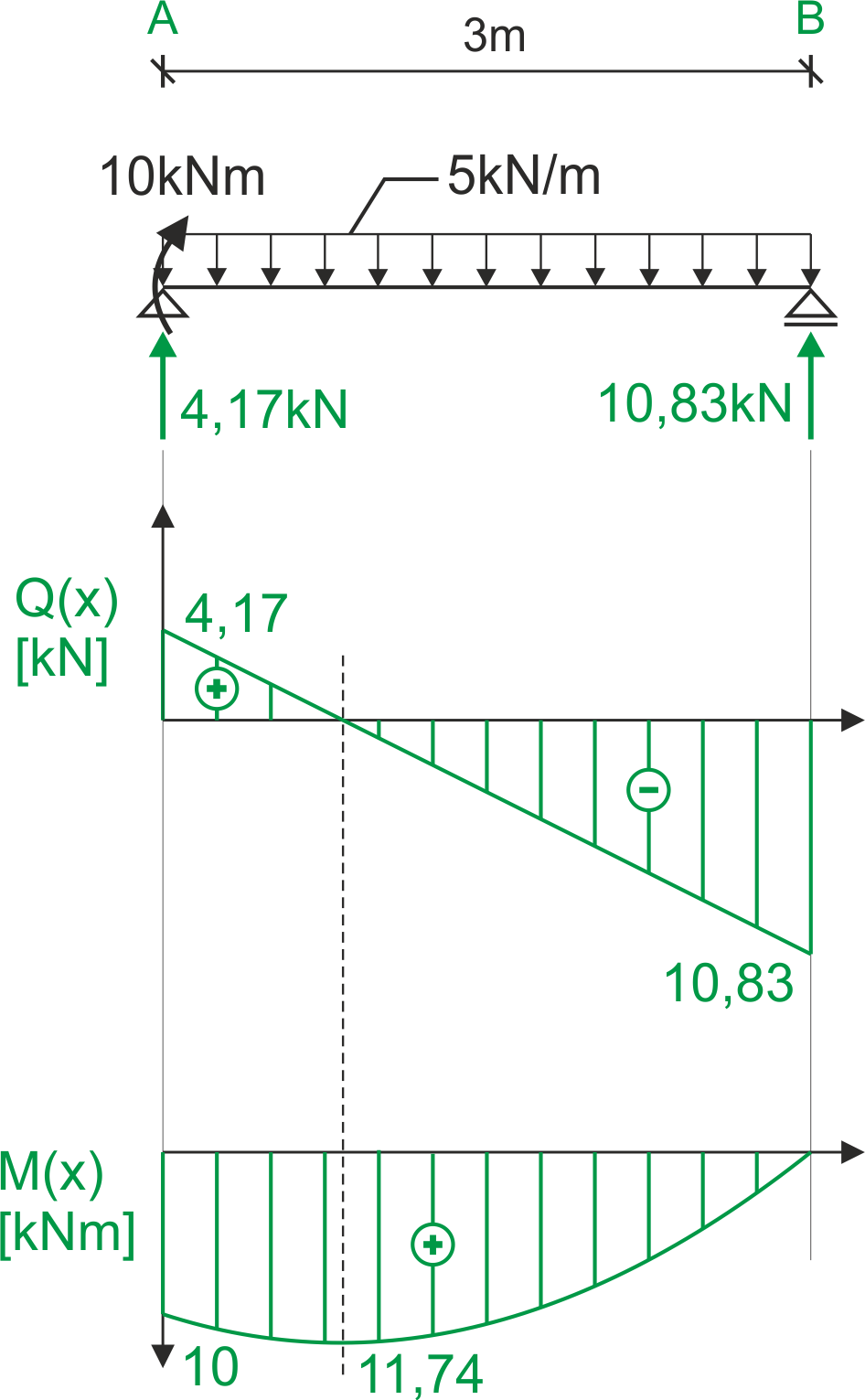
&Q_{AB}=4.17-5x & Q_{AB}=0\\
&Q_A(0)=4.17\ kN & x=0.834\ m\\
&Q_B(3)=-10.83\ kN\\
&M_{AB}=10+4.17x-5x\cdot \frac{x}{2}\\
&M_A(0)=10\ kNm & M_B(3)=0\ kNm\\
&M_{max}(0.834)=11.739\approx 11.74\ kNm
\end{aligned}
\begin{aligned}\\
&Q_{AB}=4.17-5x & Q_{AB}=0\\
&Q_A(0)=4.17\ kN & x=0.834\ m\\
&Q_B(3)=-10.83\ kN\\
&M_{AB}=10+4.17x-5x\cdot \frac{x}{2}\\
&M_A(0)=10\ kNm & M_B(3)=0\ kNm\\
&M_{max}(0.834)=11.739\approx 11.74\ kNm
\end{aligned}
Shear force and bending moment diagram
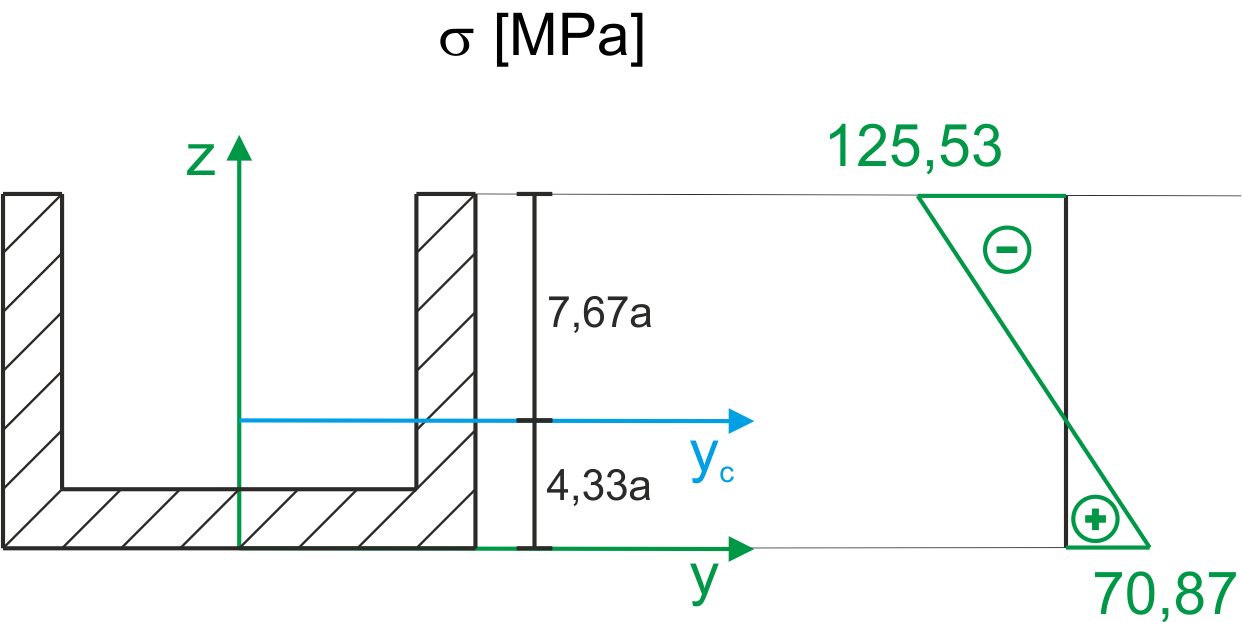
Dimensioning
\begin{aligned}\\ &k_r=120\ MPa & k_c=160\ MPa\\ &z_1=6a & A_1=12a\cdot 16a=192a^2\\ &z_2=a & A_2=10a\cdot 12a=120a^2\\ &z_c=\frac{z_1\cdot A_1-z_2\cdot A_2}{A_1-A_2}=4.33a\\ &I_{y_c}=\frac{16\cdot 12^3}{12}+192(6-4.33)^2-[\frac{12\cdot 10^3}{12}+120(7-4.33)^2]=984a^4\\ \end{aligned}The distance from the center of gravity to the upper fibers is greater, so the stresses on the upper fibers will be greater. The upper fibers are compressed, and the lower ones are subjected to tension. Higher compressive stresses on the upper fibers meet with higher compressive strength, and (lower) tensile stresses meet with lower tensile strength. Therefore, we cannot unequivocally determine which condition will be decisive, so both conditions should be checked.
\begin{aligned}\\ &W_g=\frac{I_{y_c}}{z_g}=\frac{984a^4}{7.67a}=128.29a^3\\ &W_d=\frac{I_{y_c}}{z_d}=\frac{984a^4}{4.33a}=227.25a^3\\ \\ &\frac{M_{max}}{W_g}\le k_c \Rightarrow \frac{11.74\cdot 10^3}{128.29a^3}\le 160\cdot 10^6\\ &a\ge 8.3\ mm\\ &\frac{M_{max}}{W_d}\le k_r \Rightarrow \frac{11.74\cdot 10^3}{227.25a^3}\le 120\cdot 10^6\\ &a\ge 7.55\ mm\\ \\ &a=9\ mm\\ &\sigma_g=\frac{11.74\cdot 10^3}{128.29\cdot (9\cdot 10^{-3})^3}=125.53\ MPa\\ &\sigma_d=\frac{11.74\cdot 10^3}{227.25\cdot (9\cdot 10^{-3})^3}=70.866\ MPa\\ \end{aligned}Stress diagram
If you have any questions, comments, or think you have found a mistake in this solution, please send us a message at kontakt@edupanda.pl.
