Solution
We encourage you to watch the solution to this example (and others) on our YouTube channel. We explain step by step how to solve this task. Watching this video will also help you understand other examples on our website.
\begin{aligned}\\ &Q(x)=-30+15x\\ &Q(x=0)=-30\ kN\\ &Q(x=6)=60\ kN\\ &Extremum \\ &Q(x)=-30+15x=0\\ &x=2[m]\\ &M(x=0)=30\cdot 6-\frac{1}{2}\cdot 15\cdot 6^2=-90\ kNm\\ &M_{max}(x-2)=30\ kNm\\ &M(x=6)=30\cdot 6-\frac{1}{2}\cdot 15\cdot 6^2=-90\ kNm\\ \end{aligned}Diagram of shear forces and bending moments
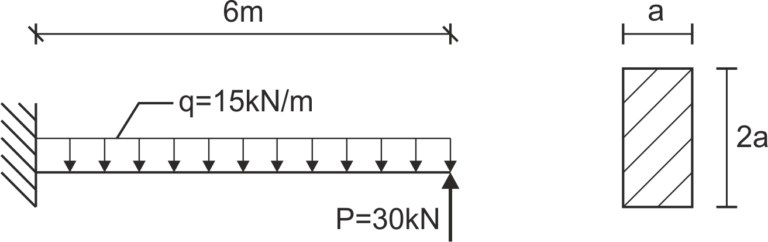
Dimensioning
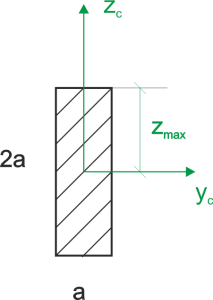 \begin{aligned}\\ &I_{y_c}=\frac{b*h^3}{12}=\frac{a*(2a)^3}{12}=\frac{2}{3}a^4 \\ &W=\frac{I_{y_c}}{z_{max}}=\frac{\frac{2}{3}a^4}{a}=\frac{2}{3}a^3\\ \end{aligned}
\begin{aligned}\\ &I_{y_c}=\frac{b*h^3}{12}=\frac{a*(2a)^3}{12}=\frac{2}{3}a^4 \\ &W=\frac{I_{y_c}}{z_{max}}=\frac{\frac{2}{3}a^4}{a}=\frac{2}{3}a^3\\ \end{aligned}
Strength condition
\begin{aligned}\\ &|\frac{M_{max}}{W}|\le k_g\\ &\frac{90*10^3}{\frac{2}{3}a^3}\le 160*10^6\\ &a\ge 0.09449 \ m\\ & a=95\ mm\\ \end{aligned}Stresses
\begin{aligned}\\ &\sigma=\frac{M}{W}=\frac{90*10^3}{\frac{2}{3}*(0.095)^3}=157.46 \ MPa\\ \end{aligned}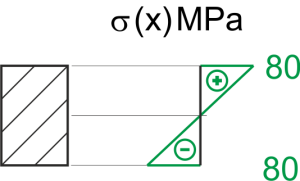
If you have any questions, comments, or think you have found a mistake in this solution, please send us a message at kontakt@edupanda.pl.
