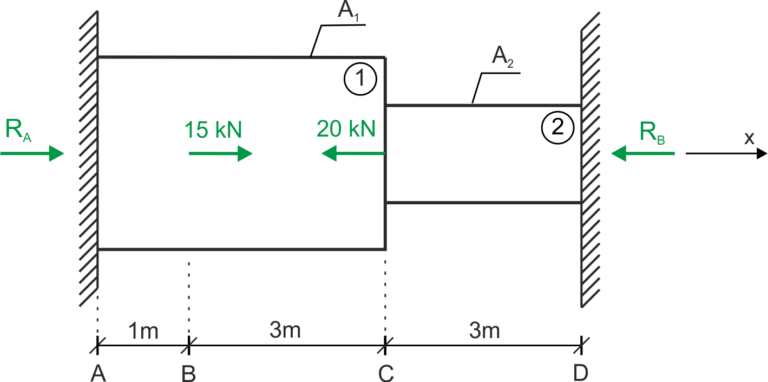
Solution
Calculation of reactions
Static equilibrium condition
\begin{aligned}
&\sum X=0 \\
&R_{A}+15-20-R_{B}=0 \\
\end{aligned}
Geometric condition
\begin{aligned}
&\Delta l_{c}=0 \\
&\Delta l_{A B}+\Delta l_{B C}+\Delta l_{C D}=0 \\
&\Delta l=\frac{N \cdot l}{E \cdot A} \\
\end{aligned}
Expanding normal forces on characteristic intervals
\begin{aligned} &N_{AB}=R_{A}\\ &N_{BC}=R_{A}+15\\ &N_{CD}=R_{A} + 15 - 20=R_{A} - 5\\ \end{aligned}
Solving the geometric condition
\begin{aligned} &\frac{R_{A}\cdot 1}{E_{1}\cdot A_{1}}+\frac{(R_{A}+15)\cdot 3}{E_{1}\cdot A_{1}}+\frac{(R_{A}-5)\cdot 3}{E_{2}\cdot A_{2}}=0\\ &\frac{R_{A}}{E_{1}\cdot 2A_{2}}+\frac{3R_{A}+45}{E_{1}\cdot 2A_{2}}+\frac{3R_{A}-15}{2E_{1}\cdot A_{2}}=0 & |\cdot E_{1}\cdot A_{2}\\ &\frac{1}{2}R_{A}+\frac{3}{2}R_{A}+22,5+\frac{3}{2}R_{A}-7,5=0\\ &3,5R_{A}=-15\\ &R_{A}=-4,286 \ kN\\ &R_{A}+15 - 20 - R_{B}=0\\ &R_{B}=-9,286 \ kN\\ \end{aligned}
After calculating the reactions RA, the final values of forces on intervals are:
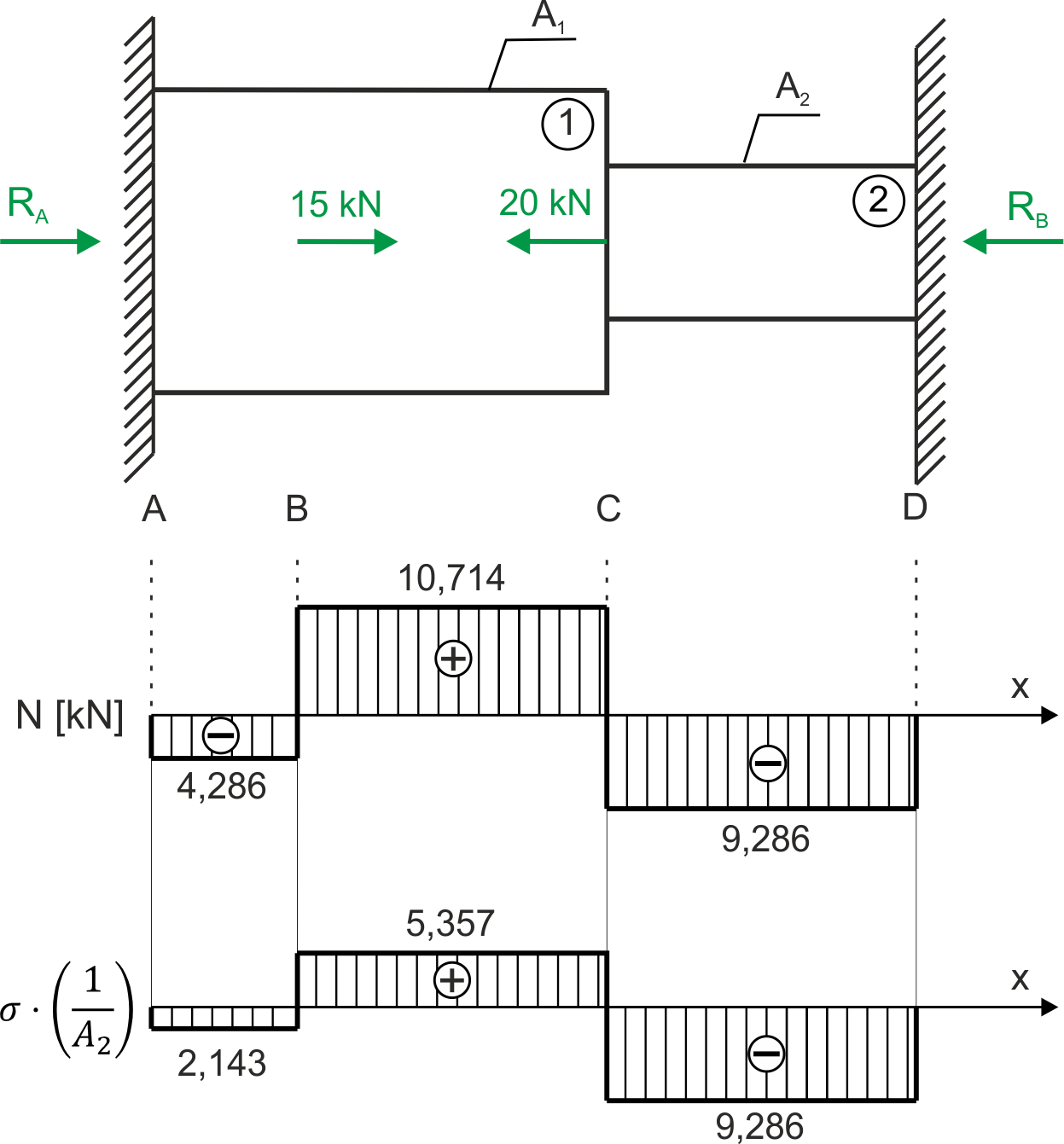
\begin{aligned} &N_{AB}=R_{A}=-4,286 \ kN\\ &N_{BC}=R_{A}+15=10,714 \ kN\\ &N_{CD}=R_{A}+15-20=R_{A}-5=-9,286 \ kN \\ \end{aligned}
Expanding normal stresses on characteristic intervals
\begin{aligned} &\sigma=\frac{N}{A}\\ &\sigma_{AB}=\frac{-4,286}{A_{1}}=\frac{-4,286}{2A_{2}}=-2,143\cdot\frac{1}{A_{2}}\\ &\sigma_{BC}=\frac{10,714}{A_{1}}=\frac{10,714}{2A_{2}}=5,357\cdot\frac{1}{A_{2}}\\ &\sigma_{CD}=\frac{9,286}{A_{2}}=9,286\cdot\frac{1}{A_{2}}\\ \end{aligned}
Graphs

If you have any questions, comments, or think you have found a mistake in this solution, please send us a message at kontakt@edupanda.pl.