Edupanda » Strength of materials » Axial Tension and Compression » Statically Indeterminate
List of examples
Example 1
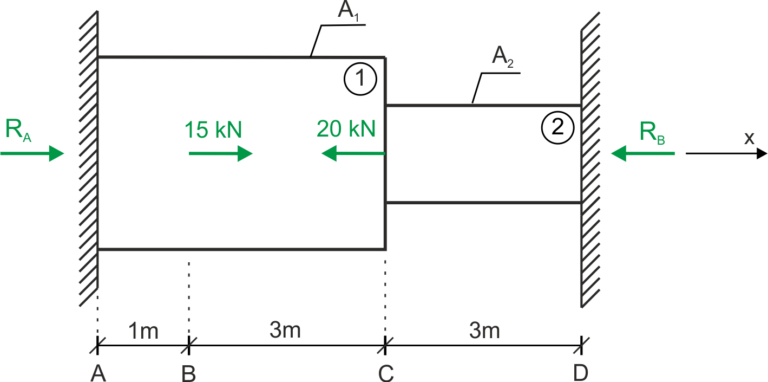
Two-level rod has been permanently fixed at end A, end D, and loaded with forces as shown in the figure. Calculate the reactions at the fixations and indicate in which part of the rod the highest stresses occur. Data: \( A_1=2\cdot A_2, 2\cdot E_1=E_2 \)
Example 2
The beam is hinged and attached with two rods and loaded constantly. Calculate the diameter of the rods based on the strength condition. Data: \( A_1 = A_2, E_1 = 2\cdot E_2, k_r = 60\ MPa, k_c = 90\ MPa \)
Example 3
The wooden beam is suspended on three bars - the first and third are made of steel, and the second is made of copper, with lengths \( l_1=3m, l_2=2m, l_3=4m \). Calculate the stresses that occur in the bars. Data: \( k_{r_s}t=120 MPa, k_{r_m}=30 MPa, A_1=A_2=2\cdot A_3, E_2=105 GPa, E_1=E_3=210 GPa\)
Example 4
Calculate the normal forces and dimension the cross-sectional area of the bar. Data: P, k
Example 5
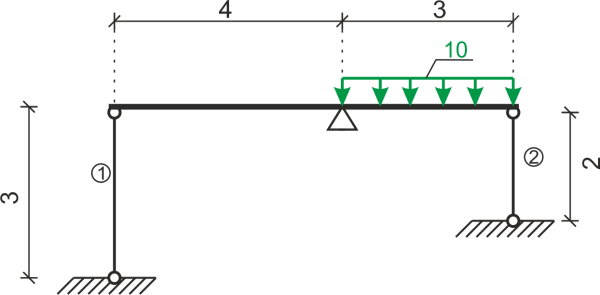
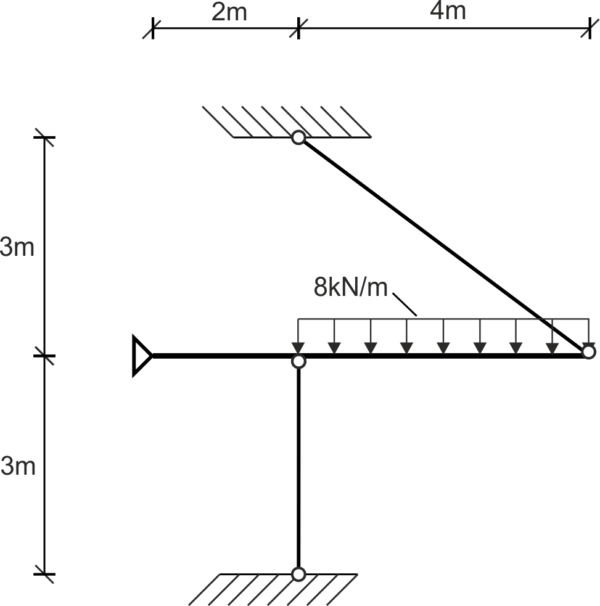
Calculate the diameter of the tendons on which the beam is supported. Data: \( E=210 GPa, A_1=A_2, k_r=100 MPa, k_c=120 MPa \)
Example 6
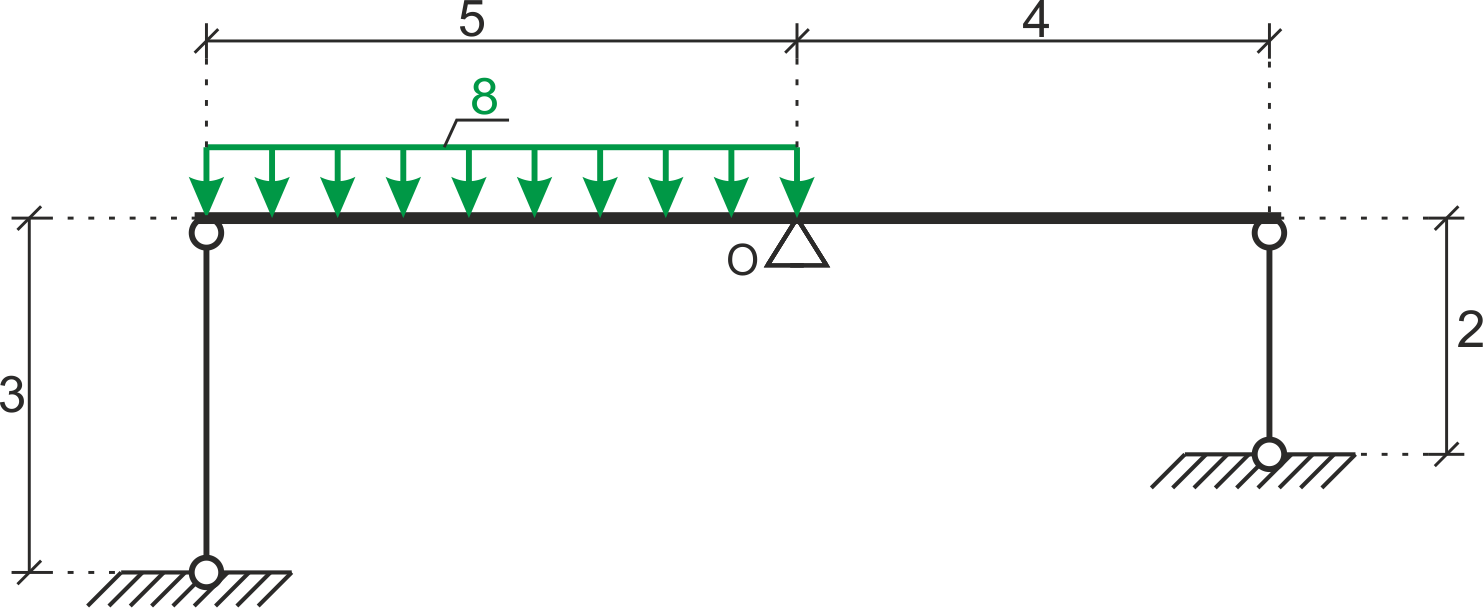
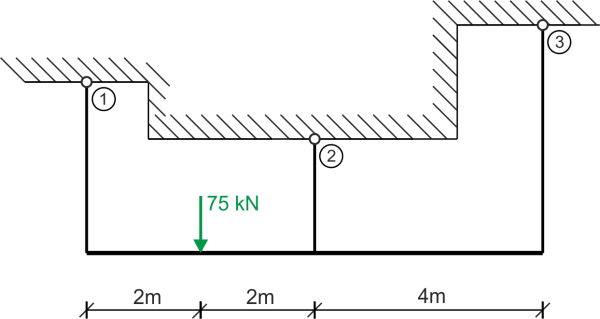
Calculate the forces in the rods supporting the beam. Data: \( A_1=A_2=A, E_1=E_2=E \)
Example 7
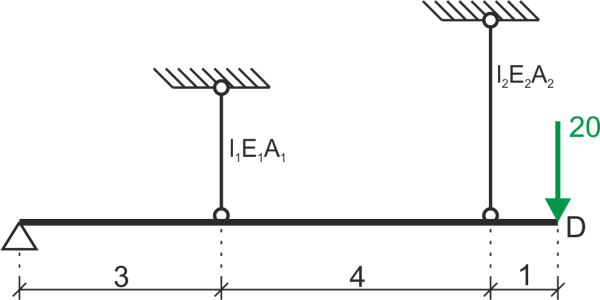
Calculate the vertical displacement of point D. Data: \( E_1=2\cdot E_2, E_1=210\ GPa, l_1=2 m, l_2=3 m, 2\cdot A_1=A_2, A_1=20 cm^2 \)
Example 8
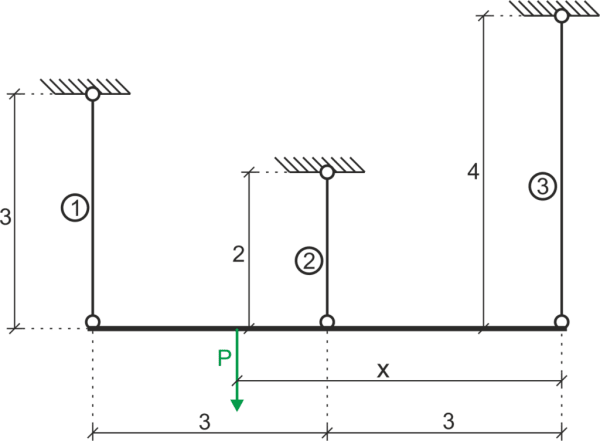
At what distance \(x\) from rod number \(3\) should force \(P\) be applied in order for the beam to move parallelly downwards. Data: \(E_1=E_3=210 GPa, E_2=110 GPa, A_1=A_2=2\cdot A_3, P=20 kN\)
Example 9
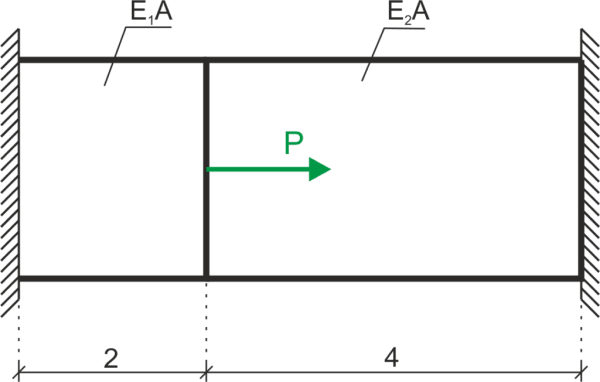
Calculate the normal forces in the bar below. Data: \(P=20 kN, E_1=2.1 \cdot 10^5 MPa, E_2=1 \cdot 10^5 MPa\)
Example 10
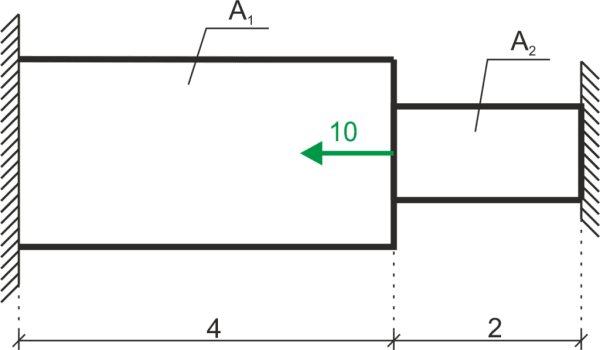
Calculate the reaction at the support on the left side from the static and thermal load, and draw a graph of normal forces. Calculate the stresses in two segments of the rod. Data:\(\Delta_T=20^o\ C, \alpha=1.2\cdot 10^{-5}, E=205\cdot 10^9, A_1=20\ cm^2, A_2=15\ cm^2\)
Example 11
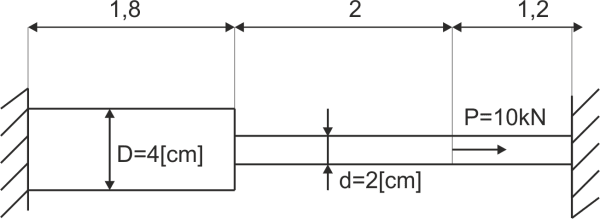
Calculate and plot the charts of normal forces, stresses and elongations for all sections of the two-stage shaft. Data as shown in the figure. The entire rod was heated by \(20^o C\). The coefficient of thermal expansion is \(\alpha =1.2\cdot 10^{-5}\).
Example 13
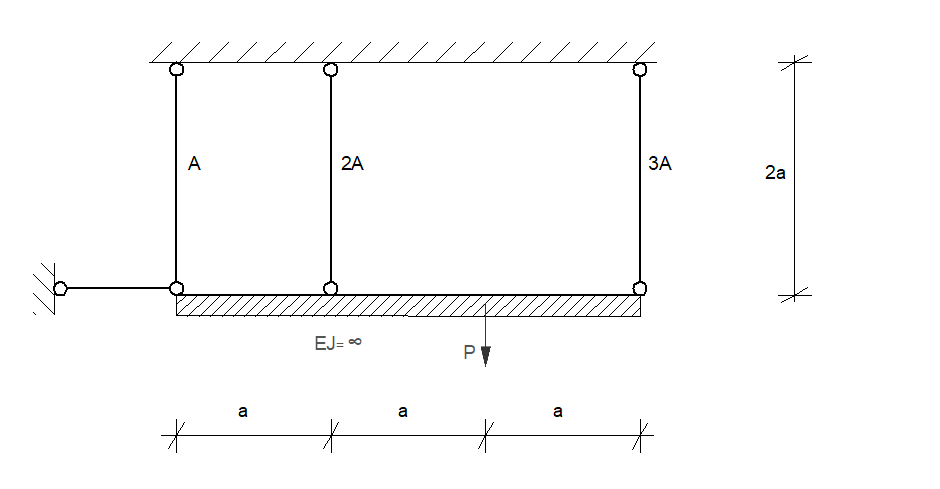
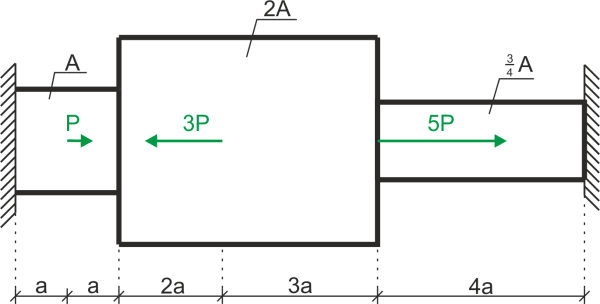
Determine the elastic load capacity \( P = P_s \) and the ultimate load capacity \( P = P_n \). Determine the ultimate load capacity using static and kinematic approaches. Check whether the obtained solution is complete. Additionally, determine the load capacity reserve factor \( m = \frac{P_n}{P_s} \). When providing the final results, assume: \( a = 1 \, \text{m} \), \( A = 4 \, \text{cm}^2 \), \( R_{pl} = 200 \, \text{MPa} \).