Solution
Classic solution
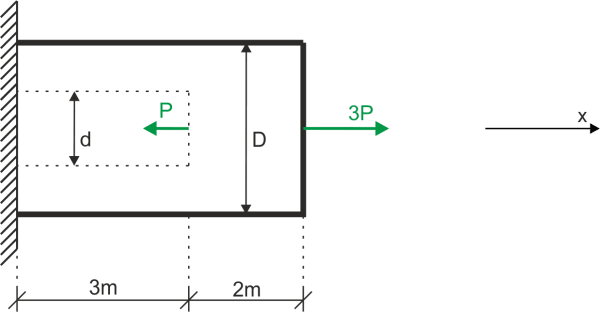
The condition of the problem is for the maximum displacement "u". It will occur at one of the characteristic points A or B. \begin{aligned} & amp;u_{B}=\Delta l_{BC}\\ & amp;u_{A}=\Delta l_{BC}+\Delta l_{AB}\\ \end{aligned} Normal forces on the characteristic intervals \begin{aligned} & amp;N_{AB}=3P\\ & amp;N_{BC}=3P-P=2P\\ \end{aligned} Normal forces on both intervals are positive, so the whole rod is being stretched, so the maximum displacement will be at its end (point A) \begin{aligned} & amp;u_{max}=0.15 \ mm=0.15\cdot 10^{-3} \ m\\ & amp;u_{max}=u_{A}=\Delta l_{BC}+\Delta l_{AB}\\ \end{aligned} Cross-sectional areas of intervals AB and BC \begin{aligned} & amp;A_{AB}=\frac{\pi D^{2}}{4}\\ & amp;A_{BC}=\frac{\pi D^{2}}{4} - \frac{\pi d^{2}}{4} = \frac{\pi(D^{2}-d^{2})}{4}\\ \end{aligned} Formula for elongation of a part of the rod \begin{aligned} & amp;\Delta l = \frac{N\cdot l}{E\cdot A}\\ \end{aligned} Finally, I write down and solve the condition of the problem \begin{aligned} & amp;\frac{3P\cdot 2}{E\cdot\frac{\pi D^{2}}{4}} + \frac{2P\cdot 3}{E\cdot\frac{\pi(D^{2}-d^{2})}{4}} \le 0.15\cdot 10^{-3} \ \ \ \ |\cdot E\pi\\ & amp;\frac{24P}{D^{2}}\cdot (D^{2}-d^{2}) + \frac{24P}{D^{2}-d^{2}}\cdot (D^{2}-d^{2}) \le 0.15\cdot 10^{-3}\cdot\pi\cdot E\cdot (D^{2}-d^{2})\\ & amp;\frac{24P}{D^{2}}\cdot D^{2} - \frac{24P}{D^{2}}\cdot d^{2} + 24P \le 0.15\cdot 10^{-3}\cdot\pi\cdot E\cdot D^{2} - 0.15\cdot 10^{-3}\cdot\pi\cdot E\cdot d^{2}\\ & amp;48\cdot 15\cdot 10^{3} - 9\cdot 10^{6}\cdot d^{2}\le 1.6\cdot 10^{6} - 40.06\cdot 10^{6}\cdot d^{2}\\ & amp;48\cdot 15\cdot 10^{3} - 1.6\cdot 10^{6} \le (-40.06\cdot 10^{6} + 9\cdot 10^{6})\cdot d^{2}\\ \\ & amp;d^{2}\ge \frac{48\cdot 15\cdot 10^{3} - 1.6\cdot 10^{6}}{-40.06\cdot 10^{6} + 9\cdot 10^{6}}\\ \\ & amp;d\ge \sqrt\frac{48\cdot 15\cdot 10^{3} - 1.6\cdot 10^{6}}{-40.06\cdot 10^{6} + 9\cdot 10^{6}}\\ & amp;d\ge 0.168 \ m\\ & amp;d\ge 16.8 \ cm\\ \end{aligned}
If you have any questions, comments, or think you have found a mistake in this solution, please send us a message at kontakt@edupanda.pl.