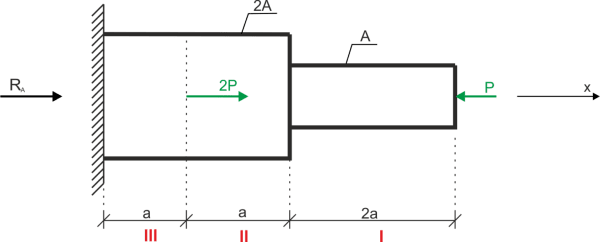
Solution
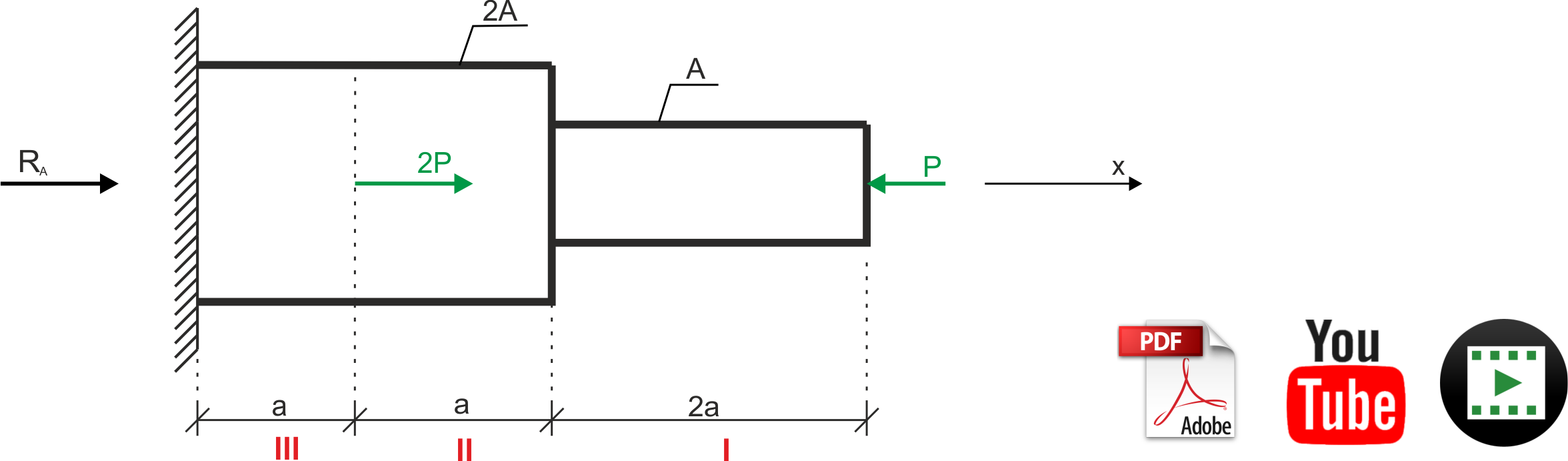
Calculation of reactions
\begin{aligned} &\sum X=0 \\ &R_{A}+2 P-P=0 \\ &R_{A}=-P \\ \end{aligned} Recording normal forces on characteristic sections
\begin{aligned} &N_{1}=-P=-10 kN \\ &N_{2}=-P=-10 kN \\ &N_{3}=-P+2 P=P=10 kN \\ \end{aligned} Strength condition
\begin{aligned} &\sigma=\left|\frac{N}{A}\right| \leq k_{r}, k_{c} \end{aligned} Compression \begin{aligned} &\frac{10 \cdot 10^{3}}{A} \leq 80 \cdot 10^{6} \\ &A \geq \frac{10 \cdot 10^{3}}{80 \cdot 10^{6}} \\ &A \geq 1.25 \times 10^{-4}\left[\mathrm{~m}^{2}\right] \end{aligned}
Tension
\begin{aligned} &\frac{10 \cdot 10^3}{2 A} \leq 60 \cdot 10^{6} \\ &2 A \geq \frac{10 \cdot 10^{3}}{60 \cdot 10^{6}} \\ &A \geq 8.33 \times 10^{-5}=0.833 \times 10^{-4}\left[\mathrm{~m}^{2}\right] \end{aligned} The tension condition decides. Dimensioning the diameter: \begin{aligned} &A \geq 1.25 \times 10^{-4} \\ &\frac{\pi d^{2}}{4} \geq 1.25 \times 10^{-4} \\ &d \geq \sqrt{\frac{4 \times 1.25 \times 10^{-4}}{\pi}} \\ &d \geq 0.0126 \\ &d=0.013 \ [m]\\ \end{aligned} Cross-sectional area at the dimensioned diameter: \begin{aligned} &A=\frac{\pi \times 0.013^{2}}{4}=1.327 \times 10^{-4} \end{aligned} Stresses on characteristic sections: \begin{aligned} \sigma_{1} &=\frac{N_{1}}{A}=-\frac{10 \times 10^{3}}{1.327 \times 10^{-4}}=-75.36 \mathrm{MPa} \\ \sigma_{2} &=\frac{N_{2}}{2 A}=-\frac{10 \times 10^{3}}{2 \times 1.327 \times 10^{-4}}=-37.68 \mathrm{MPa} \\ \sigma_{3} &=\frac{N_{3}}{2 A}=\frac{10 \times 10^{3}}{2 \times 1.327 \times 10^{-4}}=37.68 \mathrm{MPa} \end{aligned} Elongations \begin{aligned} &\Delta l=\frac{N \times l}{E \times A} \\ &\Delta l_{1}=\frac{N_{1} \times l_{1}}{E \times A}=\frac{-10 \times 10^{3} \times 2 \times 1}{2.1 \times 10^{11} \times 1.327 \times 10^{-4}}=-7.18 \times 10^{-4}[\mathrm{~m}]=-7.18 \times 10^{-4}[\mathrm{~mm}]=-0.718[\mathrm{~mm}] \\ &\Delta l_{1}=\frac{N_{1} \times l_{1}}{E \times 2 A}=\frac{-10 \times 10^{3} \times 1 \times 1}{2.1 \times 10^{11} \times 2 \times 1.327 \times 10^{-4}}=-1.79 \times 10^{-4}[\mathrm{~m}]=-0.179[\mathrm{~mm}] \\ &\Delta l_{1}=\frac{N_{1} \times l_{1}}{E \times 2 A}=\frac{10 \times 10^{3} \times 2 \times 1}{2.1 \times 10^{11} \times 2 \times 1.327 \times 10^{-4}}=1.79 \times 10^{-4}[\mathrm{~m}]=0.179[\mathrm{~mm}] \end{aligned} Summary: \begin{aligned} &N_{1}=10 kN \\ &N_{2}=-10 kN \\ &N_{3}=10 kN \\ &\sigma_{1}=-75.36 \mathrm{MPa} \\ &\sigma_{2}=-37.68 \mathrm{MPa} \\ &\sigma_{3}=37.68 \mathrm{MPa} \\ &\Delta l_{3}=0.179 \mathrm{~mm} \\ &\Delta l_{2}=-0.179 \mathrm{~mm} \\ &\Delta l_{1}=-0.718 \mathrm{~mm} \\ \end{aligned} Displacements \begin{aligned} &u_{III}=\Delta l_{3}=0.179 \mathrm{~mm} \\ &u_{II}=\Delta l_{3}+\Delta l_{2}=0.179-0.179=0 \mathrm{~mm} \\ &u_I=\Delta l_{3}+\Delta l_{2}+\Delta l_{1}=-0.718 \mathrm{~mm} \end{aligned} Graphs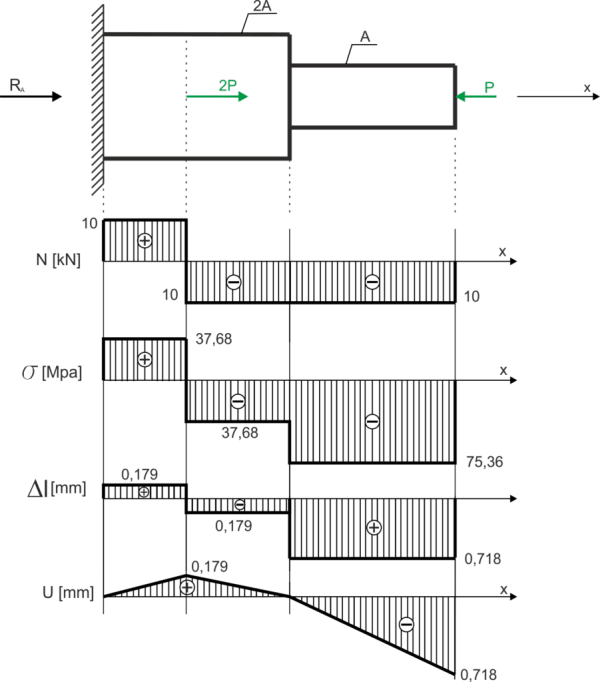
If you have any questions, comments, or think you have found a mistake in this solution, please send us a message at kontakt@edupanda.pl.