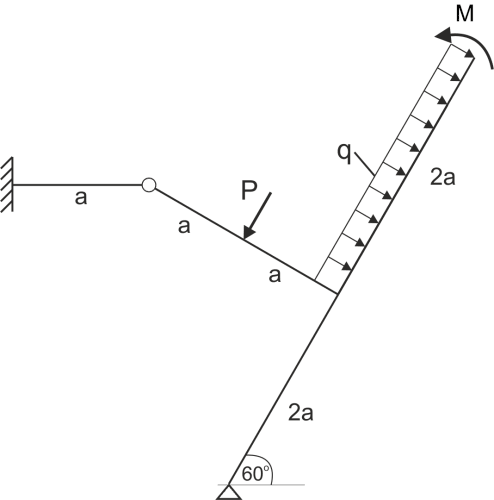
Solution
Classic Solution
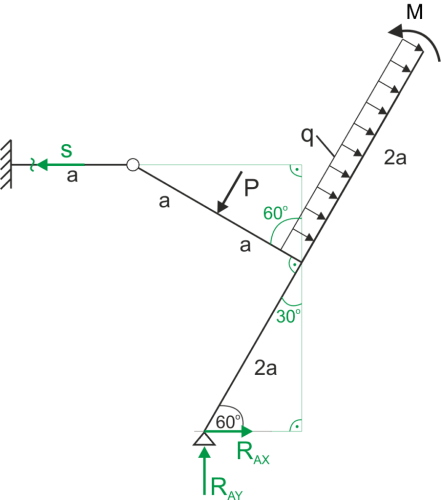 Force in the rod
\begin{aligned} & \sum{M_A}=0\\ & -Pa+2qa\cdot 3a-M-S(2a\cdot sin60+2a\cdot cos60)=0\\ & S=\frac{-Pa+2qa\cdot 3a-M}{(2a\cdot sin60+2a\cdot cos60)}\\ & S=\frac{-15\cdot 1 + 2\cdot 8\cdot 3 - 6}{2\cdot\frac{\sqrt 3}{2}+2\cdot\frac{1}{2}}=9.88 \ kN\\ & S=9.88 kN\\ \end{aligned}
Diameter from strength condition
\begin{aligned} & \sigma=|\frac{N}{A}|\le k_{r},k_{c}\\ & A=\frac{\pi d^{2}}{4}\\ & N=9.88\cdot 10^{3} \ N\\ & k_{r}=80 \ MPa\\ & \frac{9.88\cdot 10^{3}}{\frac{\pi d^{2}}{4}} \le 80\cdot 10^{6}\\ & \frac{9.88\cdot 10^{3}\cdot 4}{80\cdot 10^{6}\cdot\pi}\le d^{2}\\ & d\ge 0.0125 \ m\\ & d\ge 1.25 \ cm\\ \end{aligned}
Rod elongation
\begin{aligned} & \Delta l=\frac{N\cdot l}{E\cdot A}\\ & A=\frac{\pi d^{2}}{4}\\ & d \ge 1.25 \ cm\\ & d=1.3 \ cm\\ & A=\frac{\pi(1.3\cdot 10^{-2})^{2}}{4}=1.33\cdot 10^{-4} \ m^{2}\\ & E=2\cdot 10^{5}\cdot 10^{6} Pa\\ & N=9.88\cdot 10^3 \ N\\ & \Delta l=\frac{9.88\cdot 10^{3}\cdot 1}{2\cdot 10^{11}\cdot 1.33\cdot 10^{-4}}=3.8\cdot 10^{-4} \ m=0.38 \ mm\\ \end{aligned}
Force in the rod
\begin{aligned} & \sum{M_A}=0\\ & -Pa+2qa\cdot 3a-M-S(2a\cdot sin60+2a\cdot cos60)=0\\ & S=\frac{-Pa+2qa\cdot 3a-M}{(2a\cdot sin60+2a\cdot cos60)}\\ & S=\frac{-15\cdot 1 + 2\cdot 8\cdot 3 - 6}{2\cdot\frac{\sqrt 3}{2}+2\cdot\frac{1}{2}}=9.88 \ kN\\ & S=9.88 kN\\ \end{aligned}
Diameter from strength condition
\begin{aligned} & \sigma=|\frac{N}{A}|\le k_{r},k_{c}\\ & A=\frac{\pi d^{2}}{4}\\ & N=9.88\cdot 10^{3} \ N\\ & k_{r}=80 \ MPa\\ & \frac{9.88\cdot 10^{3}}{\frac{\pi d^{2}}{4}} \le 80\cdot 10^{6}\\ & \frac{9.88\cdot 10^{3}\cdot 4}{80\cdot 10^{6}\cdot\pi}\le d^{2}\\ & d\ge 0.0125 \ m\\ & d\ge 1.25 \ cm\\ \end{aligned}
Rod elongation
\begin{aligned} & \Delta l=\frac{N\cdot l}{E\cdot A}\\ & A=\frac{\pi d^{2}}{4}\\ & d \ge 1.25 \ cm\\ & d=1.3 \ cm\\ & A=\frac{\pi(1.3\cdot 10^{-2})^{2}}{4}=1.33\cdot 10^{-4} \ m^{2}\\ & E=2\cdot 10^{5}\cdot 10^{6} Pa\\ & N=9.88\cdot 10^3 \ N\\ & \Delta l=\frac{9.88\cdot 10^{3}\cdot 1}{2\cdot 10^{11}\cdot 1.33\cdot 10^{-4}}=3.8\cdot 10^{-4} \ m=0.38 \ mm\\ \end{aligned}
If you have any questions, comments, or think you have found a mistake in this solution, please send us a message at kontakt@edupanda.pl.