Zginanie poprzeczne - wstęp
Zginanie poprzeczne dotyczy sytuacji, w której element konstrukcyjny, taki jak belka, jest poddawany obciążeniom działającym prostopadle do jego osi podłużnej. Kluczowy aspekt analizy zginania poprzecznego obejmuje wyznaczenie naprężeń tnących (inaczej stycznych, ścinających). Siły tnące powstają równolegle do obciążenia poprzecznego i powodują naprężenia styczne w materiale.
Z tego kursu dowiesz się
- jak wyznaczyć reakcje i narysować wykresy sił wewnętrznych,- jak narysować wykres naprężeń stycznych,
- jak narysować wykres naprężeń normalnych (powtórka zginania prostego),
- jak na podstawie naprężeń normalnych i tnących obliczyć naprężenia zredukowane
z hipotezy Hubera Missesa Henkyego,
- jak zwymiarować grubość spoiny łączącej półkę dwuteownika z środnikiem,
W zginaniu poprzecznym naprężenia styczne można wyrazić wzorem (podajemy dwa warianty, w zależności od kierunku działania siły poprzecznej – oczywiście może działać w jednej i drugiej płaszczyźnie na raz):
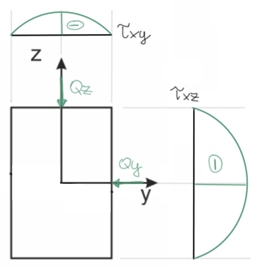
$$\tau_{xz} = \frac{-Q_z \cdot S_y}{I_y \cdot b}$$ $$\tau_{xy} = \frac{-Q_y \cdot S_z}{I_z \cdot h}$$
gdzie:
• \( \tau \) to naprężenie styczne,
• \( Q \) to siła tnąca w danym przekroju,
• \( S \) to statyczny moment przekroju powyżej punktu, w którym obliczane jest naprężenie styczne
( \( S_y \) – moment względem osi y, \( S_z \) – względem osi z),
• \( I \) to moment bezwładności całego przekroju,
• \( b/h \) to szerokość/wysokość przekroju w punkcie, gdzie obliczane jest naprężenie.
Rys1. Wykres naprężeń stycznych dla przekroju prostokątnego
Maksymalne naprężenia styczne występują zazwyczaj w osi obojętnej przekroju belki.
Mając policzone naprężenia normalne (zginanie proste) i naprężenia styczne (zginanie poprzeczne) można zajmować się kolejnymi zagadnieniami, m.in. można obliczyć z hipotez wytężeniowych naprężenia zredukowane – najczęściej według hipotezy Hubera-Misesa-Henckyego lub Tresci-Guesta. Można również narysować kostkę naprężeń dla danego punktu przekroju i policzyć naprężenia minimalne oraz maksymalne dla tego punktu.
Do dyspozycji masz kursy wideo oraz szeroką bazę zadań z rozwiązaniami dla każdego rodzaju zginania osobno.
ZOBACZ TEŻ

