Twierdzenia o prętach zerowych
Z tego tekstu dowiesz się jakie są twierdzenia o prętach zerowych oraz znajdziesz przykłady kratownic z wyznaczeniem prętów zerowych
Kratownica (ang. truss) – układ złożony z prętów prostych, połączonych między sobą w węzłach przegubowo, obciążony siłami skupionymi w przegubach. Połączenia przegubowe ciągną za sobą konsekwencję taką, że siły przekrojowe w prętach kratownicy to wyłącznie siły osiowe (podłużne, normalne).
Kratownica (ang. truss) – układ złożony z prętów prostych, połączonych między sobą w węzłach przegubowo, obciążony siłami skupionymi w przegubach. Połączenia przegubowe ciągną za sobą konsekwencję taką, że siły przekrojowe w prętach kratownicy to wyłącznie siły osiowe (podłużne, normalne).
Twierdzenia o prętach zerowych
Twierdzenie I
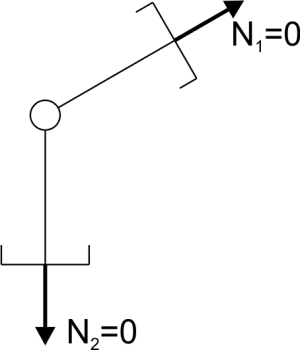
Jeżeli w węźle kratownicy schodzą się 2 pręty i węzeł jest nieobciążony, to siły wewnętrzne w obu prętach są równe zeru.
Twierdzenie II
Jeżeli w węźle kratownicy schodzą się 2 pręty i węzeł jest obciążony siłą leżącą na kierunku jednego z nich, to siła wewnętrzna w drugim pręcie jest równa zero.
Twierdzenie III
Jeżeli w węźle kratownicy schodzą się 3 pręty, z których dwa leżą na tej samej prostej i węzeł jest nieobciążony, to siła w trzecim pręcie jest równa zero.Przykład 1
Przykład 2
Treść
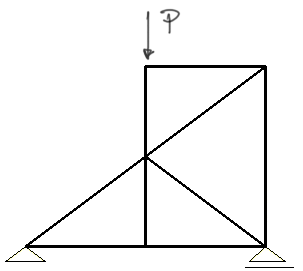
Dla kratownicy jak na rysunku podaj ile jest prętów zerowych?
Rozwiązanie
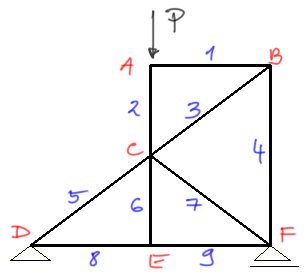
Krok 1
Ponumerowanie prętów, oznaczenie węzłów.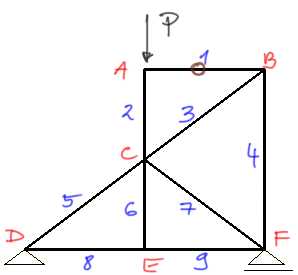
Krok 2
Zauważam z II twierdzenia, że pręt nr 1 jest zerowy i zaznaczam ten pręt na brązowo "0".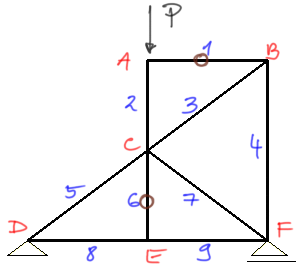
Krok 3
Równocześnie zauważam, że z III twierdzenia pręt numer 6 jest zerowy - zaznaczam go.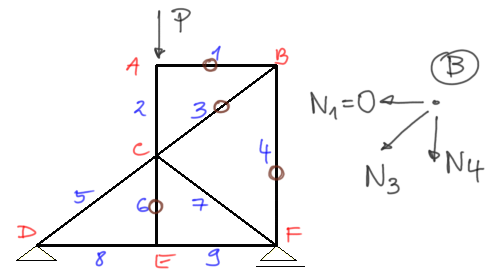
Krok 4
I teraz najciekawszy krok, musimy spojrzeć na węzeł B, jeżeli wytypowaliśmy wcześniej pręt nr 1 jako zerowy, to teraz można powiedzieć że do węzła B schodzą się dwa, a nie trzy pręty (bo jeden w tym przypadku jest zerowy). W takim razie z pierwszego twierdzenia - jeżeli w węźle schodzą się dwa pręty i jest on nieobciążony to obydwa pręty są zerowe - pręty numer 3 i 4 będą zerowe.Przykład 3
Treść
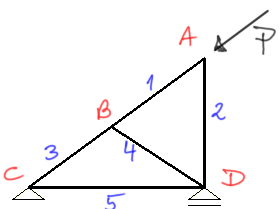
Dla kratownicy jak na rysunku podaj ile jest prętów zerowych?
Rozwiązanie
Krok 1
Ponumerowanie prętów, oznaczenie węzłów.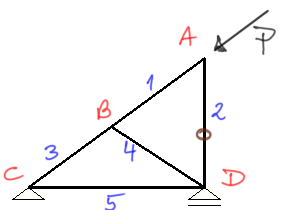
Krok 2
Zauważam z II twierdzenia, że pręt nr 2 jest zerowy i zaznaczam ten pręt na brązowo "0".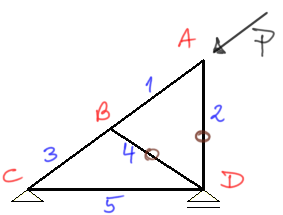
Krok 3
Równocześnie zauważam, że z III twierdzenia pręt numer 4 jest zerowy (patrzę na węzeł B).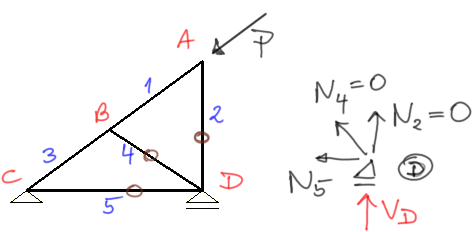
Krok 4
Z uwagi na to że pręty 2 i 4 są zerowe, to jak spojrzymy na węzeł D, zobaczymy, że działa na niego teraz siła w pręcie 5 oraz reakcja VD.Z twierdzenia II określamy, że pręt nr 5 jest zerowy.
Przykład 4
Treść
Dla kratownicy jak na rysunku podaj ile jest prętów zerowych?
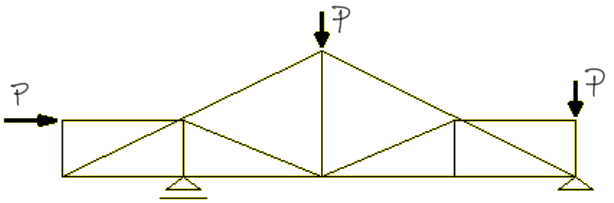
Rozwiązanie
Krok 1
Ponumerowanie prętów, oznaczenie węzłów.
Krok 2
Zauważam z II twierdzenia, że pręty: nr 5 oraz nr 6 są zerowe. Zauważam również, że pręt nr 11 jest zerowy (z III twierdzenia) i zaznaczam te pręty na brązowo "0".
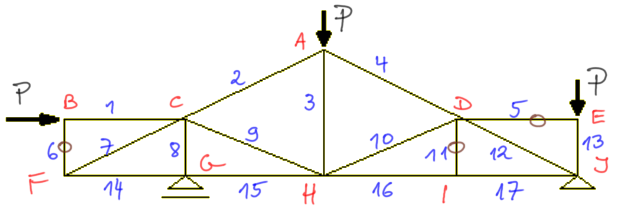
Krok 3
Usuwam z kratownicy myślowo zerowe pręty i zauważam, że w węźle F zostały dwa pręty i jest on nieobciążony - wobec tego pręt nr 7 i nr 14 są zerowe (I twierdzenie).
W węźle D zostały trzy pręty, z czego dwa są współliniowe i węzeł jest nieobciążony, więc z III twierdzenia pręt nr 10 jest zerowy.
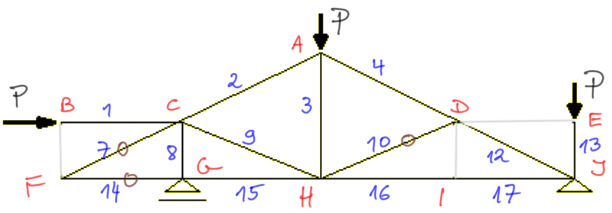
Krok 4
Usunąłem myślowo kolejne zerowe pręty i teraz zauważam, że w węźle G ma zastosowanie II twierdzenie. W węźle są dwa pręty, z czego reakcja VG działa pionowo, czyli współliniowo do pręta 8, a więc pręt nr 15 będzie zerowy.
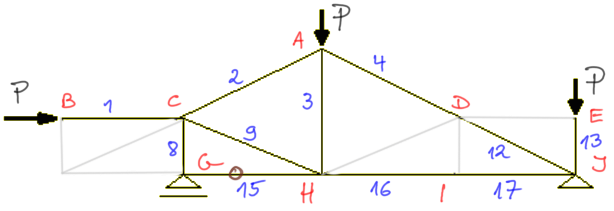
Tym sposobem aż 7 prętów wytypowaliśmy jako pręty zerowe.
↓ odnośnik do bazy zadań z rozwiązaniami oraz do kursów wideo ↓
ZOBACZ TEŻ
Teoria
Nagrania
ŁUKASZ
CICHOWICZ
Korepetytor
150 PLN
60 MIN
Zobacz mój profil na
