Skręcanie prętów kołowych
Z tego tekstu dowiesz się:
- kiedy mamy do czynienia ze skręcaniem
- jak może być rysowany moment skręcający
- o konwencji dodatniego znakowania momentu skręcającego
- czym jest i jaki jest wzór na:
a) kąt skręcenia
b) moment bezwładności na skręcanie dla przekroju kołowego i pierścieniowego
c) jednostkowy kąt skręcenia
d) kąt odkształcenia postaciowego
e) naprężenia styczne
f) wskaźnik wytrzymałości na skręcanie
- jaka jest postać tensora naprężenia i odkształcenia dla pręta skręcanego
- jak obliczyć energię sprężystą dla pręta skręcanego
- jak wygląda kostka naprężeń oraz koło Mohra dla przypadku czystego ścinania
Znajdziesz również przykłady obliczeniowe oraz
↓ odnośnik do bazy zadań z rozwiązaniami oraz do kursów wideo ↓
- kiedy mamy do czynienia ze skręcaniem
- jak może być rysowany moment skręcający
- o konwencji dodatniego znakowania momentu skręcającego
- czym jest i jaki jest wzór na:
a) kąt skręcenia
b) moment bezwładności na skręcanie dla przekroju kołowego i pierścieniowego
c) jednostkowy kąt skręcenia
d) kąt odkształcenia postaciowego
e) naprężenia styczne
f) wskaźnik wytrzymałości na skręcanie
- jaka jest postać tensora naprężenia i odkształcenia dla pręta skręcanego
- jak obliczyć energię sprężystą dla pręta skręcanego
- jak wygląda kostka naprężeń oraz koło Mohra dla przypadku czystego ścinania
Znajdziesz również przykłady obliczeniowe oraz
↓ odnośnik do bazy zadań z rozwiązaniami oraz do kursów wideo ↓
Kiedy mamy do czynienia ze skręcaniem?
Ze skręcaniem mamy do czynienia wówczas, gdy układ sił zewnętrznych redukuje się do momentu skręcającego (czyli momentu, którego wektor jest równoległy do wzdłużnej osi pręta, tj. prostopadły do przekroju). W tym wstępie teoretycznym zajmiemy się skręcaniem prętów kołowych, jest to szczególny przypadek skręcania dla którego zastosowanie ma zasada płaskich przekrojów Bernoulliego, która mówi że przekrój płaski i prostopadły do osi pręta, po deformacji pozostaje płaski i prostopadły do odkształconej osi pręta.Moment skręcający może być rysowany na trzy sposoby:


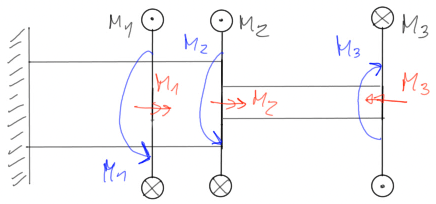
Rys1. Sposoby zaznaczania momentu skręcającego
Konwencja dodatniego znakowania momentu skręcającego

Rys2. Konwencja dodatniego znakowania momentu skręcającego
Przy założeniu:
- materiału pręta jako liniowo sprężysty o stałych materiałowych E oraz v,
- małych przemieszczeń,
- zastosowania płaskich przekrojów Bernoulliego,
możemy przyjąć obraz deformacji jak na rys3. poniżej.
Przeanalizujmy ruch linii AB przed przyłożeniem momentu skręcającego i po przyłożeniu momentu.
Rys3. Obraz obrotu pręta kołowego
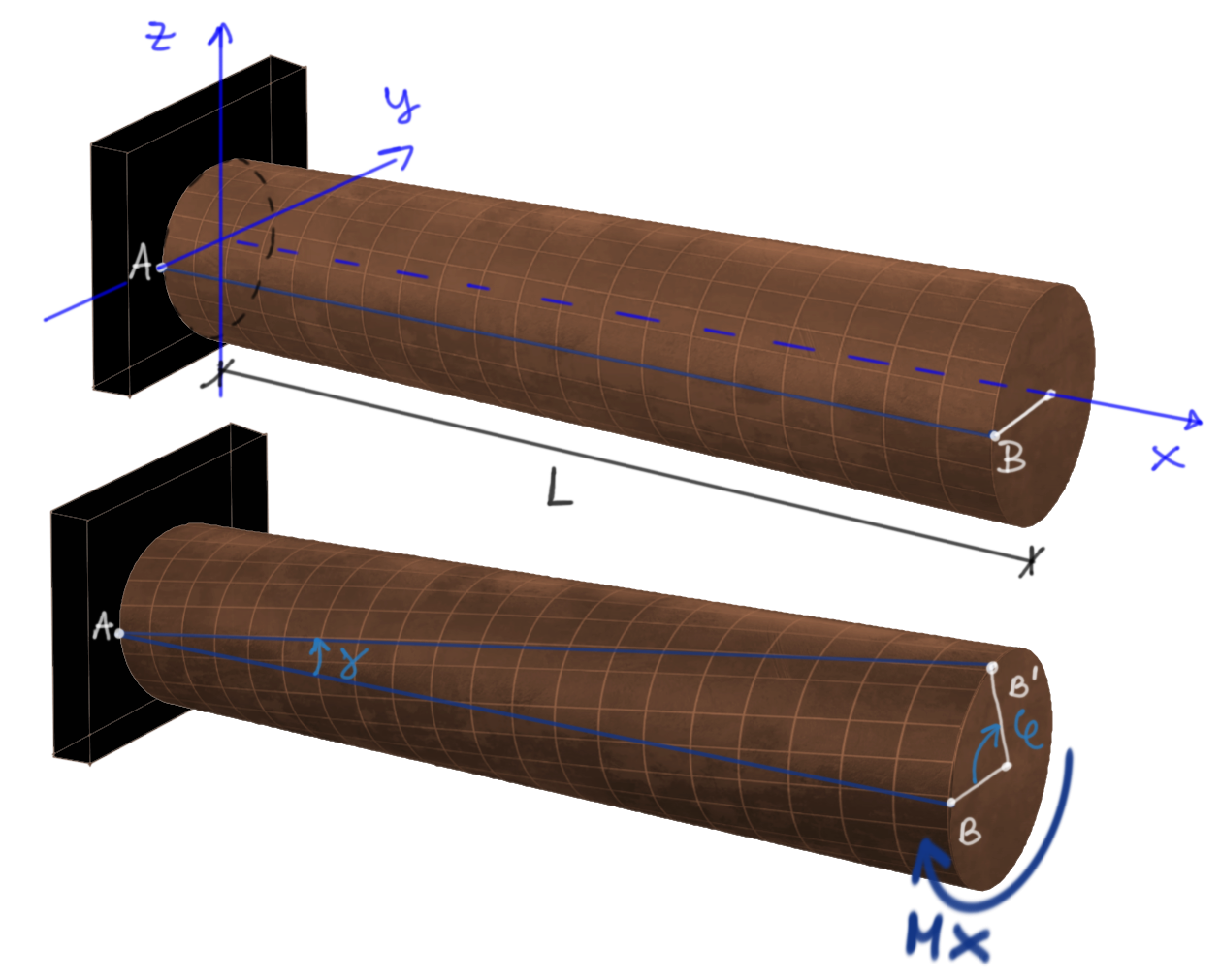
\(\boldsymbol{\varphi}\) - kąt skręcenia w przekroju końcowym
\(\boldsymbol{\gamma}\) - kąt odkształcenia postaciowego
\(\boldsymbol{\theta}\) - kąt skręcenia na jednostkę długości
Kąt skręcenia w przekroju końcowym względem utwierdzenia obliczamy ze wzoru:
\begin{aligned} &\varphi=\frac{\mathrm{M}_{\mathrm{x}} \cdot \mathrm{L}}{\mathrm{G} \cdot \mathrm{I}_s}\\ \end{aligned} Gdyby pręt był obciążony ciągłym, a nie skupionym momentem skręcającym, wówczas musimy skorzystać z takiej wersji wzoru: \begin{aligned} &\varphi=\int_{x_p}^{x_k} \frac{M_x(x)}{G \cdot I_s} d x \end{aligned}
Tego typu zadania (z obciążeniem ciągłym momentem skręcającym) znajdziesz w naszym kursie online z wytrzymałości materiałów
w dziale skręcanie statycznie wyznaczalne przykłady 9-12 oraz
w dziale skręcanie statycznie niewyznaczalne, przykład 9.
gdzie:Mx - moment skręcający lub Mx(x) - funkcja momentu skręcającego
L - długość pręta, lub części pręta
G - moduł Kirchoffa (stała materiałowa)
Is - moment bezwładności na skręcanie
Moment bezwładności na skręcanie
Dla przekroju kołowego lub pierścieniowego moment bezwładności na skręcanie jest równy biegunowemu momentowi bezwładności. Biegunowy moment bezwładności to po prostu suma momentów bezwładności dwóch prostopadłych osi przechodzących przez punkt (biegun, tutaj środek ciężkości) i jest to po prostu:- dla przekroju pierścieniowego \[ I_s=\frac{\pi \cdot\left(D^4-d^4\right)}{32} \] D - zewnętrzna średnica pierścienia,
d - wewnętrzna średnica pierścienia
- dla przekroju kołowego \[ I_s=\frac{\pi \cdot D^4}{32} \]
Kąt skręcenia na jednostkę długości (jednostkowy kąt skręcenia)
liczymy ze wzoru: \[ \theta=\frac{\mathrm{M}_{\mathrm{x}}}{\mathrm{G} \cdot \mathrm{I}_{\mathrm{s}}} \]Kąt odkształcenia postaciowego \( \gamma \)
Wzór na kąt odkształcenia postaciowego możemy wyprowadzić wprost z Rys3.Po pierwsze założyliśmy na początku małe przemieszczenia, a więc kąt \( \gamma \) będzie bardzo mały, ponieważ jest to stosunek niewielkiego wycinku łuku z obwodu przekroju BB' pręta do wielokrotnie większej długości samego pręta. Dla małych kątów wystarczające jest przybliżenie: \( \gamma = tg(\gamma) \) , czyli że wartość kąta gamma jest równa swojemu tangensowi.
Po drugie szybkie przypomnienie z matematyki - wzór na wycinek łuku (interesuje nas wycinek łuku między B a B'): \[Ł=\frac{\varphi}{360^{\circ}} 2 \pi r = \varphi \cdot r\] pierwsza postać jeśli wstawiamy kąt skręcenia w stopniach, druga - z której korzystamy - jeśli wstawiamy w radianach, czyli jednostce podstawowej.
Wobec powyższego \[ \gamma=\frac{BB'}{L}=\frac{\varphi \cdot r}{L} \] jest to kąt odkształcenia postaciowego na powierzchni pręta (na obwodzie przekroju), jeśli za \( \rho \) przyjmiemy dowolną promieniową odległość od środka ciężkości do punktu przekroju, wówczas wzór możemy zapisać: \[ \gamma=\frac{BB'}{L}=\frac{\varphi \cdot \rho}{L} \]

Rys4. Przekrój kołowy, współrzędna \( \rho \)
Naprężenia styczne

Rys5. Rozkład naprężeń stycznych w przekroju kołowym i pierścieniowym
Wzór na wypadkowe naprężenia styczne w dowolnym punkcie przekroju poprzecznego wygląda nastepujaco: $$ \tau=\frac{\mathrm{M}_{\mathrm{x}}}{\mathrm{I}_{\mathrm{S}}} \cdot \rho=\frac{\mathrm{M}_{\mathrm{X}}}{\mathrm{W}_{\mathrm{s}}(\rho)} $$ Najczęściej będziemy potrzebowali obliczyć maksymalne naprężenia styczne, czyli naprężenia na obwodzie koła lub pierścienia, a więc dla \(\rho=R=\frac{D}{2}\).
Wskaźnik wytrzymałości na skręcanie dla skrajnych włókien : \(\mathrm{W}_{\mathrm{S}}=\frac{\mathrm{I}_{\mathrm{S}}}{\mathrm{R}}\)
Dla przekroju kołowego: \(\mathrm{W}_{\mathrm{s}}=\frac{\frac{\pi \cdot \mathrm{D}^4}{32}}{\frac{\mathrm{D}}{2}}=\boldsymbol{\frac{\pi \cdot \mathrm{D}^3}{16}} \)
Dla przekroju pierścieniowego: \(\mathrm{W}_{\mathrm{s}}=\frac{\frac{\pi \cdot\left(\mathrm{D}^4-\mathrm{d}^4\right)}{32}}{\frac{\mathrm{D}}{2}}=\boldsymbol{\frac{\pi \cdot\left(\mathrm{D}^4-\mathrm{d}^4\right)}{16 \cdot \mathrm{D}}} \)
Jednak raczej nie ma sensu zapamiętywanie wzorów na wskaźnik wytrzymałości na skręcanie, wystarczy znać wzór na moment bezwładności i skorzystać z wyrażenia które jest zapisane na początku na naprężenia styczne.
Jeżeli potrzebujemy składowe naprężenia stycznego \(\tau_{x z}\) oraz \(\tau_{x y}\) to musimy mieć określone współrzędne punktu na przekroju \((y, z)\) w którym mamy policzyć te naprężenia i wówczas:
\begin{aligned} & \tau_{\mathrm{xz}}=\frac{\mathrm{M}_{\mathrm{x}}}{\mathrm{I}_{\mathrm{s}}} \cdot \mathrm{y} \\ & \tau_{\mathrm{xy}}=\frac{\mathrm{M}_{\mathrm{x}}}{\mathrm{I}_{\mathrm{s}}} \mathrm{z} \end{aligned} oraz oczywiście zachodzi: \(\tau=\sqrt{\tau_{x z}^2+\tau_{x y}^2}\)
Znając naprężenia można policzyć odkształcenia postaciowe z zależności \[\gamma_{xz}=\frac{\tau_{xz}}{G}, \gamma_{xy}=\frac{\tau_{xy}}{G} \]
Postać tensora naprężenia i odkształcenia dla pręta skręcanego:
\begin{aligned} T_\sigma=\left[\begin{array}{ccc} 0 & \tau_{x y} & \tau_{x z} \\ \tau_{y x} & 0 & 0 \\ \tau_{z x} & 0 & 0 \end{array}\right] \quad T_{\varepsilon}=\left[\begin{array}{ccc} 0 & \gamma_{x y} & \gamma_{x z} \\ \gamma_{y x} & 0 & 0 \\ \gamma_{z x} & 0 & 0 \end{array}\right] \end{aligned}Energia sprężysta dla pręta skręcanego o przekroju kołowym lub pierścieniowym
Dla pręta o jednym przedziale charakterystycznym: \[U=\int_0^L \frac{M_x^2(x)}{2 G J_s} d x\] Dla pręta o większej liczbie przedziałów (jeśli zmienia się na długości pręta przekrój lub materiał lub jeżeli w różnych miejscach mamy obciążenie momentami skręcającymi) wówczas musimy zrobić sumowanie po wszystkich przedziałach charakterystycznych: \[U=\sum_{i=1}^n \int_0^{L_i} \frac{M_{x i}^2(x)}{2 G J_{s i}} d x\]Kostka naprężeń dla przypadku czystego ścinania, naprężenia i kierunki główne, koło Mohra
Rozważmy jakie naprężenia powstają pod wpływem działania momentu skręcającego Mx w punkcie A przekroju poprzecznego.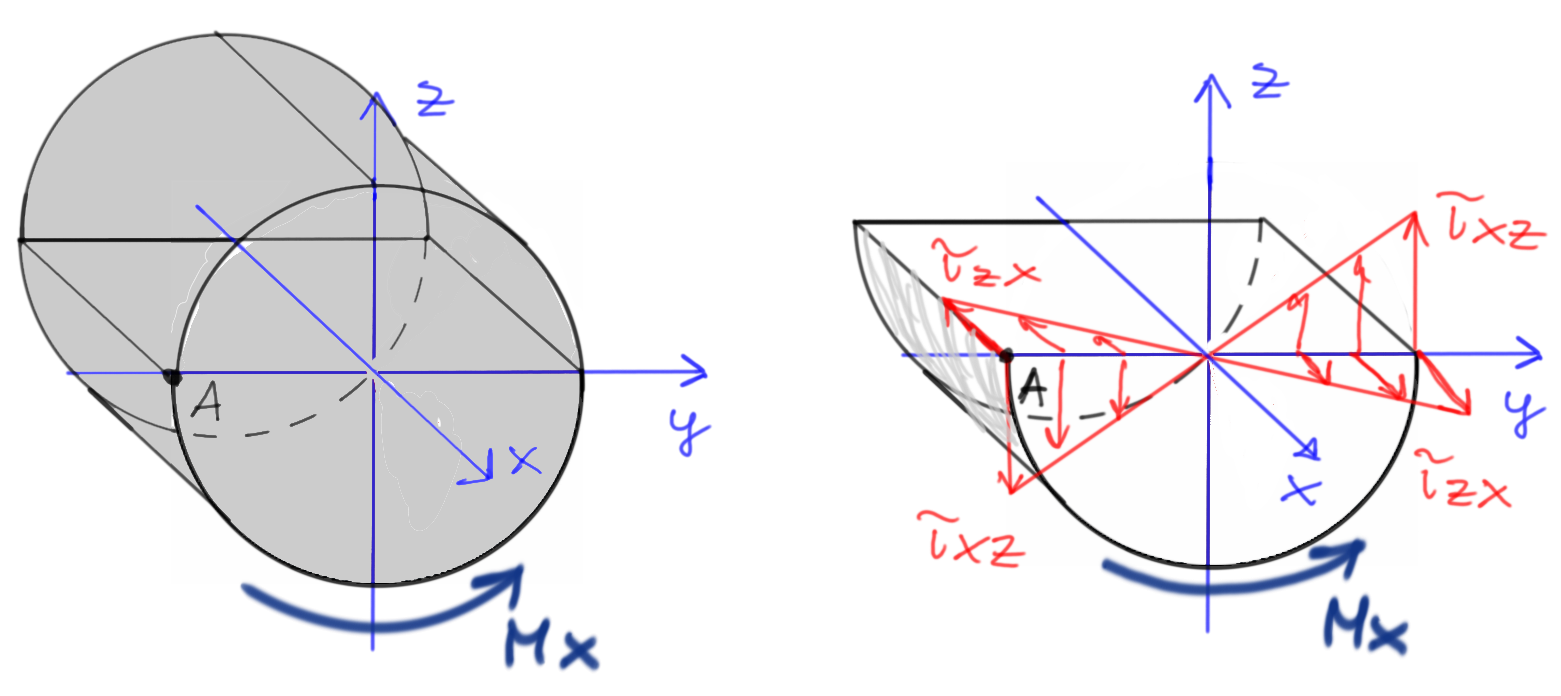
Rys6. Naprężenia ścinające w punkcie A
\(\operatorname{tg} \alpha_1=\frac{-\tau_{x z}}{\sigma_z-\sigma_1}, \operatorname{tg} \alpha_2=\frac{-\tau_{x z}}{\sigma_z-\sigma_2}\)
\(\operatorname{tg} \alpha_1=\frac{-\tau_{\mathrm{xz}}}{-\sigma_1}=\frac{-\tau_{\mathrm{xz}}}{-\tau_{\mathrm{xz}}}\), a ponieważ sama wartość \(\tau_{\mathrm{xz}}\) w naszym przykładzie jest ujemna (patrz pierwsza linijka pod Rys6.) to ostatecznie \(\operatorname{tg} \alpha_1=-1\), a więc \(\alpha_1=-45{ }^{\circ}\)
Analogicznie wyjdzie \(\alpha_2=45{ }^{\circ}\)
Obracamy oś pozioma, dodatni kąt obrotu oznacza obrót w kierunku od osi poziomej do pionowej, czyli przeciwnie do ruchu wskazówek zegara

Rys7. Kostki naprężeń
koło Mohra

Rys8. Koło Mohra - przypadek czystego ścinania
Przykład 1
Przykład 1
Treść
Dwustopniowy wałek o wymiarach d=6 cm został przymocowany trwale lewym końcem i obciążony momentami 20 oraz 30 kNm jak na rysunku. Przyjąć G=80 GPa. Obliczyć i narysować wykresy momentów skręcających, naprężeń stycznych oraz kąta skręcenia: \( M(x), \tau(x), \varphi(x) . \)

Rozwiązanie
Wyznaczamy momenty skręcające na przedziałach charakterystycznych
\begin{aligned} &M_{B C}=-20 \mathrm{kNm} \\ &M_{A B}=-20+30=10 \mathrm{kNm} \\ \end{aligned}Wyznaczamy maksymalne naprężenia styczne
\begin{aligned} &\tau=\frac{M_{S}}{W_{S}} \\ &W_{S}=\frac{\pi \cdot d^{3}}{16} \\ \end{aligned}W tym celu potrzebujemy policzyć wskaźniki wytrzymałości na skręcanie
\begin{aligned} &W_{S_{B C}}=\frac{\pi \cdot 0,06^{3}}{16}=4,24 \cdot 10^{-5} \mathrm{~m}^{3} \\ &W_{S_{A B}}=\frac{\pi \cdot 0,12^{3}}{16}=3,39 \cdot 10^{-4} \mathrm{~m}^{3} \\ \end{aligned}Teraz możemy obliczyć naprężenia
\begin{aligned} &\tau=\frac{M_{B C}}{W_{S_{B C}}}=\frac{-20 \cdot 10^{3}}{4,24 \cdot 10^{-5}}=-471,57 \mathrm{MPa} \\ &\tau=\frac{M_{A B}}{W_{S_{A B}}}=\frac{10 \cdot 10^{3}}{3,39 \cdot 10^{-4}}=29,5 \mathrm{MPa} \end{aligned}Następnie obliczymy kąty skręcenia w przekrojach charakterystycznych względem utwierdzenia
\begin{aligned} &\varphi=\frac{M_{S} \cdot l}{G \cdot I} \\ \end{aligned}Do tego potrzebujemy momenty bezwładności na skręcanie
\begin{aligned} &I=\frac{\pi \cdot d^{4}}{32} \\ &I_{B C}=\frac{\pi \cdot 0,06^{4}}{32}=1,27 \cdot 10^{-6} \mathrm{~m}^{4} \\ &I_{A B}=\frac{\pi \cdot 0,12^{4}}{32}=2,04 \cdot 10^{-5} \mathrm{~m}^{4} \\ \end{aligned}Przykładowo: kąt skręcenia przekroju C względem przekroju B obliczymy w taki sposób:
\[ \varphi_{B C}=\frac{M_{S_{B C}} \cdot l_{B C}}{G \cdot I_{B C}} \]Jednak zacznijmy od utwierdzenia w punkcie A, gdzie wiemy, że kąt obrotu jest równy 0
\[ \varphi_{A}=0 \]Następnie kąt obrotu przekroju B względem A:
\[ \varphi_{B}=\varphi_{A}+\varphi_{A B} \]oraz całkowity kąt skręcania, czyli suma kąta skręcenia w B oraz skręcenia przekroju C względem B
\[ \varphi_{C}=\varphi_{B}+\varphi_{B C} \]Obliczenia
\begin{aligned} &\varphi_{A B}=\frac{10 \cdot 10^{3} \cdot 3}{80 \cdot 10^{9} \cdot 2,04 \cdot 10^{-5}}=0,0183 \text{ rad} \\ &\varphi_{B C}=\frac{-20 \cdot 10^{3} \cdot 2}{80 \cdot 10^{9} \cdot 1,27 \cdot 10^{-6}}=-0,3937\text{ rad} \\ &\varphi_{B}=0+0,0183=0,0183 \text{ rad} \\ &\varphi_{C}=0,0183-0,3937=-0,3754 \text{ rad} \end{aligned}Po wykonaniu wszystkich obliczeń możemy narysować wykresy momentów skręcających, naprężeń stycznych i kąta skręcenia
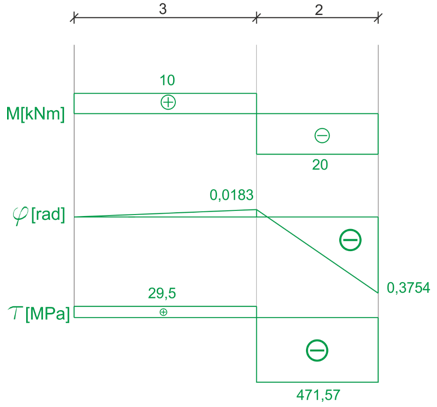
Przykład 2
Przykład 3
ZOBACZ TEŻ

