Metoda Wereszczagina
Jeśli interesuje Cię wyprowadzenie metody Wereszczagina - zajrzyj do naszego słownika pojęć.
Jeśli mamy przecałkować ze sobą figury (czyli w praktyce funkcje), z których:
- jedna jest albo może być paraboliczna (funkcja kwadratowa, pod obciążeniem ciągłym stałym) - to będzie wykres w stanie Początkowym (od zadanych obciążeń),
- druga jest nieparaboliczna - to będzie stan jednostkowy, przy liczeniu przemieszczeń będzie to wykres od siły jednostkowej przyłożonej w miejscu i na kierunku szukanego przemieszczenia - Zobacz więcej na ten temat - Metoda Maxwella-Mohra,
to wynik takiego całkowania możemy sprowadzić do wzoru:
\(u=\Omega \cdot \eta\)
gdzie:
\( \Omega \) - pole figury na wykresie momentów w stanie P,
\( \eta \) - rzędna na wykresie w stanie jednostkowym w miejscu (na wysokości) środka ciężkości figury ze stanu P.
Poniższy obrazek przedstawia to graficznie.

Oznacza to, że zwrot przemieszczenia będzie przeciwny, niż zwrot założonej przez nas siły jednostkowej.
W przypadku pionowego przemieszczenia w punkcie B przyjęta została siła jednostkowa ze zwrotem w dół,
przemieszczenie wyszło ujemne, co oznacza, że w rzeczywistości będzie do góry.
Zwrot siły jednostkowej odpowiadającej szukanemu kątowi obrotu w punkcie A założony został prawoskrętny moment.
2) Przy całkowaniu metodą Wereszczagina musimy zwracać uwagę na to czy pola całkowanych figur są po tej samej stronie pręta, czy po przeciwnej.
Jeśli są po tej samej to wynik tego pojedynczego całkowania jest dodatni, jeżeli po przeciwnych - to ujemny.
3) Kolejną ważną rzeczą jest rozkład na figury proste. Zarówno wykres ze stanu P, jak i ze stanu jednostkowego jeśli jest bardziej skomplikowaną figurą niż: prostokąt, trójkąt prostokątny, parabola możemy i będziemy rozkładać myślowo na figury proste.
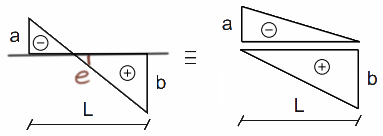
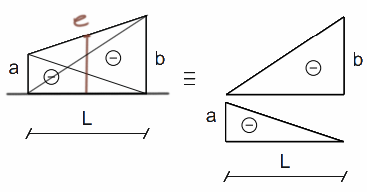
Czasami przydaje się obliczenie wartości w połowie wykresu, jak to można łatwo zrobić?
Jeżeli wykres zmienia się liniowo, to w połowie jest średnia arytmetyczna z dwóch skrajnych liczb, przykładowo:
- na rys1. \( e=\frac{-a+b}{2} \),
- na rys2. \(e=\frac{-a-b}{2} \),
Jeżeli wykres zmienia się parabolicznie, to do tej średniej należy dodać lub odjąć od niej wartość \( f=\frac{q\cdot l^2}{8} \) reprezentującą wybrzuszenie paraboli, która powstaje jeśli mamy obciążenie ciągłe na elemencie.
A więc \( e=\frac{a+b}{2}\pm \frac{q\cdot l^2}{8} \), gdzie to czy damy plus czy minus zależy od tego czy działanie obciążenia ciągłego powoduje, że parabola jest wypukła, czy wklęsła, zresztą zobaczcie na przykładach niżej.
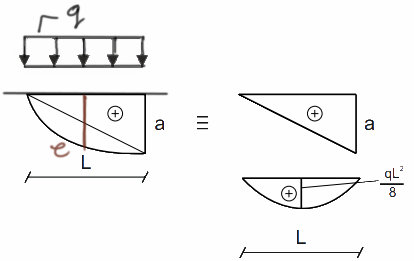
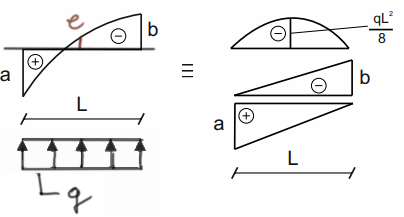
\( e=\frac{a+(-b)}{2}-\frac{q\cdot l^2}{8} \)
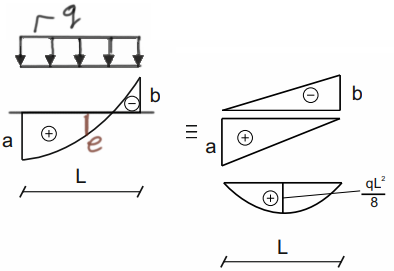
\( e=\frac{a+(-b)}{2}+\frac{q\cdot l^2}{8} \)
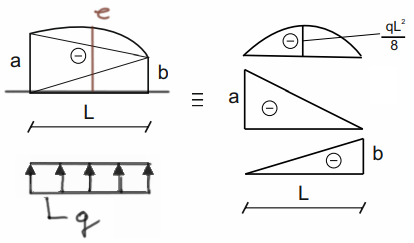
\( e=\frac{-a+(-b)}{2}-\frac{q\cdot l^2}{8} \)
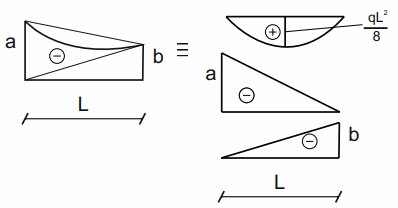
\( e=\frac{-a+(-b)}{2}+\frac{q\cdot l^2}{8} \)
Na koniec jeszcze jeden, kłopotliwy na początku przypadek. Musimy pamiętać, że jeżeli obciążenie ciągłe nie jest prostopadłe do pręta, to przy rozkładzie na figury proste licząc wysokość paraboli \( f \) jako długość bierzemy długość działania obciążenia ciągłego, a nie długość pręta!.
Zobacz przykład poniżej
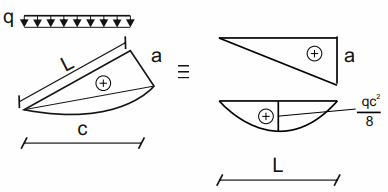
\( e=\frac{0+a}{2}+\frac{q\cdot c^2}{8} \)
W zasadzie wszystkie możliwe całkowania możemy obliczyć wykorzystując cztery wzory:
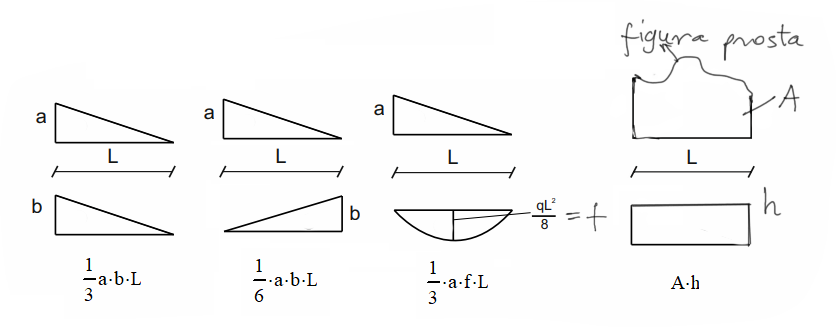
Przy każdym całkowaniu zwracamy uwagę na znaki figur całkowanych, jeśli są takie same to mamy wynik dodatni, jeśli przeciwne to ujemny.
Wzory:
1) Trójkąt z trójkątem -> jeżeli wysokości są po tej samej stronie to według wzoru by było \( \Omega \cdot \eta = \frac{1}{2}\cdot a \cdot L\cdot \frac{2}{3} \cdot b \) co nam daje po skróceniu gotowy wzór \( \frac{1}{3} \cdot a \cdot b \cdot L \)
2) Trójkąt z trójkątem, wysokości po przeciwnych stronach -> \( \Omega \cdot \eta = \frac{1}{2}\cdot a \cdot L\cdot \frac{1}{3} \cdot b=\frac{1}{6} \cdot a \cdot b \cdot L \)
3) Trójkąt (dowolnie obrócony) z parabolą -> Uwaga! Przy całkowaniu z parabolą pole musi być liczone z paraboli, a rzędna z drugiej figury. \( \Omega \cdot \eta = \frac{2}{3}\cdot f \cdot L\cdot \frac{1}{2} \cdot a=\frac{1}{3} \cdot a \cdot F \cdot L \)
4) Dowolna figura z prostokątem -> z definicji będzie to pole tej dowolnej figury razy rzędna z prostokąta, który wszędzie ma tą samą wysokość "h". \( \Omega \cdot \eta = A \cdot h \)
Przy czym dowolna figura, po rozkładzie na figury proste to będzie:
- trójkąt
- prostokąt
- albo parabola
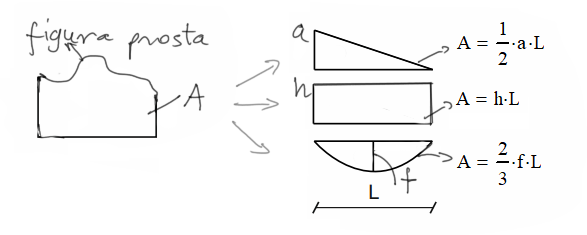
Niektórzy korzystają z większej ilości wzorów, można ich mnożyć na prawdę wiele, jednak te cztery plus rozkład na figury proste wystarczą żeby poradzić sobie z każdą sytuacją.
Oczywiście liczenie z definicji i nie pamiętanie gotowych wzorów też zawsze będzie ok.
Dla przykładu poniżej tablica z książki dra Mariana Palucha
(AGH, Podstawy Mechaniki Budowli, Kraków 2003)

Ze wzoru trzeciego od góry i trzeciego od dołu szczególnie często korzystają studenci AGH :)
A więc Wereszczagin zauważył, że
\(u=\int \frac{M_g \cdot M_1}{E I} \cdot d x=\frac{1}{E I} \cdot \Omega \cdot \eta\)Jeśli mamy przecałkować ze sobą figury (czyli w praktyce funkcje), z których:
- jedna jest albo może być paraboliczna (funkcja kwadratowa, pod obciążeniem ciągłym stałym) - to będzie wykres w stanie Początkowym (od zadanych obciążeń),
- druga jest nieparaboliczna - to będzie stan jednostkowy, przy liczeniu przemieszczeń będzie to wykres od siły jednostkowej przyłożonej w miejscu i na kierunku szukanego przemieszczenia - Zobacz więcej na ten temat - Metoda Maxwella-Mohra,
to wynik takiego całkowania możemy sprowadzić do wzoru:
\(u=\Omega \cdot \eta\)
gdzie:
\( \Omega \) - pole figury na wykresie momentów w stanie P,
\( \eta \) - rzędna na wykresie w stanie jednostkowym w miejscu (na wysokości) środka ciężkości figury ze stanu P.
Poniższy obrazek przedstawia to graficznie.

Kilka praktycznych uwag
1) Co właściwie oznacza, jeśli przemieszczenie wychodzi ujemne?Oznacza to, że zwrot przemieszczenia będzie przeciwny, niż zwrot założonej przez nas siły jednostkowej.
W przypadku pionowego przemieszczenia w punkcie B przyjęta została siła jednostkowa ze zwrotem w dół,
przemieszczenie wyszło ujemne, co oznacza, że w rzeczywistości będzie do góry.
Zwrot siły jednostkowej odpowiadającej szukanemu kątowi obrotu w punkcie A założony został prawoskrętny moment.
2) Przy całkowaniu metodą Wereszczagina musimy zwracać uwagę na to czy pola całkowanych figur są po tej samej stronie pręta, czy po przeciwnej.
Jeśli są po tej samej to wynik tego pojedynczego całkowania jest dodatni, jeżeli po przeciwnych - to ujemny.
3) Kolejną ważną rzeczą jest rozkład na figury proste. Zarówno wykres ze stanu P, jak i ze stanu jednostkowego jeśli jest bardziej skomplikowaną figurą niż: prostokąt, trójkąt prostokątny, parabola możemy i będziemy rozkładać myślowo na figury proste.
Przykłady podziału na figury proste
Trapez 1
Przykład podobny do tego który rozważaliśmy przy wyprowadzaniu metody Wereszczagina.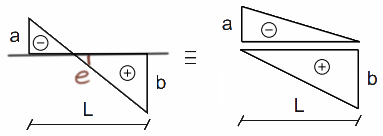
Trapez 2
Teraz figura którą rzeczywiście na pierwszy rzut oka identyfikujemy jako trapez.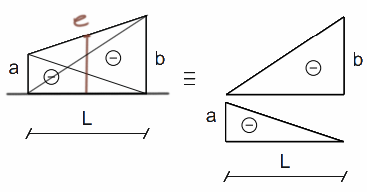
Czasami przydaje się obliczenie wartości w połowie wykresu, jak to można łatwo zrobić?
Jeżeli wykres zmienia się liniowo, to w połowie jest średnia arytmetyczna z dwóch skrajnych liczb, przykładowo:
- na rys1. \( e=\frac{-a+b}{2} \),
- na rys2. \(e=\frac{-a-b}{2} \),
Jeżeli wykres zmienia się parabolicznie, to do tej średniej należy dodać lub odjąć od niej wartość \( f=\frac{q\cdot l^2}{8} \) reprezentującą wybrzuszenie paraboli, która powstaje jeśli mamy obciążenie ciągłe na elemencie.
A więc \( e=\frac{a+b}{2}\pm \frac{q\cdot l^2}{8} \), gdzie to czy damy plus czy minus zależy od tego czy działanie obciążenia ciągłego powoduje, że parabola jest wypukła, czy wklęsła, zresztą zobaczcie na przykładach niżej.
Trójkąt-parabola
Działanie obciążenia ciągłego powoduje, że parabola jest wypukła, więc \( e=\frac{0+a}{2}+\frac{q\cdot l^2}{8} \)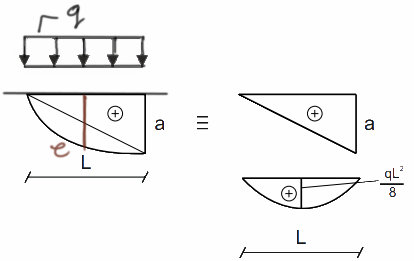
Trapez paraboliczny 1
Teraz coś ciekawszego i w zasadzie nic trudniejszego niż dwa kolejne przypadki nie może się zdarzyć.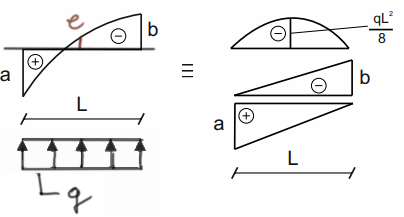
\( e=\frac{a+(-b)}{2}-\frac{q\cdot l^2}{8} \)
Trapez paraboliczny 2
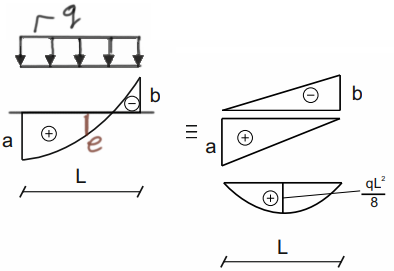
\( e=\frac{a+(-b)}{2}+\frac{q\cdot l^2}{8} \)
Trapez paraboliczny 3
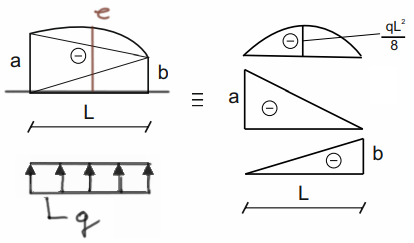
\( e=\frac{-a+(-b)}{2}-\frac{q\cdot l^2}{8} \)
Trapez paraboliczny 4
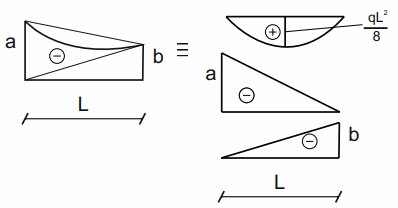
\( e=\frac{-a+(-b)}{2}+\frac{q\cdot l^2}{8} \)
Trapez paraboliczny 5
Myślę że zasada działania jest już jasna.Na koniec jeszcze jeden, kłopotliwy na początku przypadek. Musimy pamiętać, że jeżeli obciążenie ciągłe nie jest prostopadłe do pręta, to przy rozkładzie na figury proste licząc wysokość paraboli \( f \) jako długość bierzemy długość działania obciążenia ciągłego, a nie długość pręta!.
Zobacz przykład poniżej
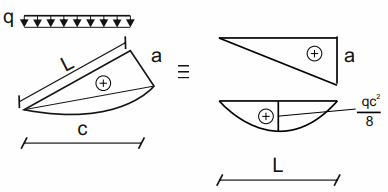
\( e=\frac{0+a}{2}+\frac{q\cdot c^2}{8} \)
Wzory/tablica Wereszczagina
Często wykorzystuje się też wyprowadzone wzory korzystając z metody Wereszczagina.W zasadzie wszystkie możliwe całkowania możemy obliczyć wykorzystując cztery wzory:
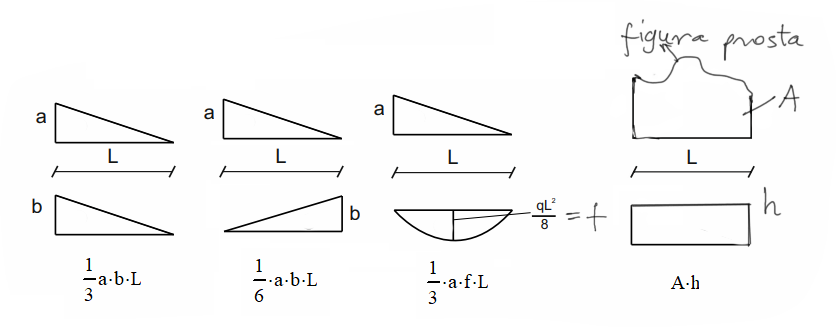
Przy każdym całkowaniu zwracamy uwagę na znaki figur całkowanych, jeśli są takie same to mamy wynik dodatni, jeśli przeciwne to ujemny.
Wzory:
1) Trójkąt z trójkątem -> jeżeli wysokości są po tej samej stronie to według wzoru by było \( \Omega \cdot \eta = \frac{1}{2}\cdot a \cdot L\cdot \frac{2}{3} \cdot b \) co nam daje po skróceniu gotowy wzór \( \frac{1}{3} \cdot a \cdot b \cdot L \)
2) Trójkąt z trójkątem, wysokości po przeciwnych stronach -> \( \Omega \cdot \eta = \frac{1}{2}\cdot a \cdot L\cdot \frac{1}{3} \cdot b=\frac{1}{6} \cdot a \cdot b \cdot L \)
3) Trójkąt (dowolnie obrócony) z parabolą -> Uwaga! Przy całkowaniu z parabolą pole musi być liczone z paraboli, a rzędna z drugiej figury. \( \Omega \cdot \eta = \frac{2}{3}\cdot f \cdot L\cdot \frac{1}{2} \cdot a=\frac{1}{3} \cdot a \cdot F \cdot L \)
4) Dowolna figura z prostokątem -> z definicji będzie to pole tej dowolnej figury razy rzędna z prostokąta, który wszędzie ma tą samą wysokość "h". \( \Omega \cdot \eta = A \cdot h \)
Przy czym dowolna figura, po rozkładzie na figury proste to będzie:
- trójkąt
- prostokąt
- albo parabola
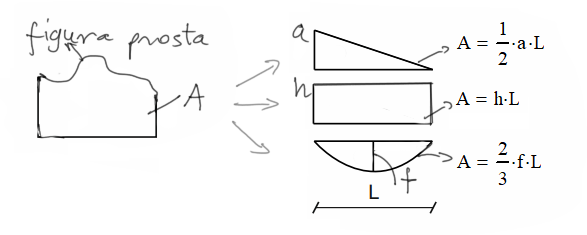
Niektórzy korzystają z większej ilości wzorów, można ich mnożyć na prawdę wiele, jednak te cztery plus rozkład na figury proste wystarczą żeby poradzić sobie z każdą sytuacją.
Oczywiście liczenie z definicji i nie pamiętanie gotowych wzorów też zawsze będzie ok.
(AGH, Podstawy Mechaniki Budowli, Kraków 2003)

Ze wzoru trzeciego od góry i trzeciego od dołu szczególnie często korzystają studenci AGH :)
Przykłady obliczania przemieszczeń w belkach z wykorzystaniem całkowania metodą Wereszczagina
ZOBACZ TEŻ

