Wytrzymałość materiałów - Metoda Maxwella – Mohra
Kurs „Metody energetyczne - Przemieszczenia w układach statycznie wyznaczalnych” skupia się na metodach energetycznych, które wykorzystują zasady zachowania energii w systemach sprężystych do przewidywania zachowania materiałów pod obciążeniem.
Metoda Maxwella-Mohra - podejście uproszczone
Metoda Maxwella-Mohra jest kolejną ważną techniką energetyczną używaną do analizy przemieszczeń w konstrukcjach. Jest to metoda bardziej ogólna, która obejmuje zarówno obciążenia mechaniczne, jak i termiczne, geometryczne oraz podpory sprężyste. Wzór Maxwella-Mohra uwzględnia wpływ wszystkich możliwych oddziaływań na konstrukcję. W tej metodzie przemieszczenia od obciążeń mechanicznych oblicza się poprzez całkowanie iloczynów funkcji momentów zginających, sił tnących i sił normalnych dla stanów początkowych i jednostkowych.
W tym podstawowym kursie zajmiemy się tylko wpływem momentów na przemieszczenie od obciążeń mechanicznych. Ponadto chcemy tutaj pokazać podejście podstawowe, w którym będziemy wykonywać całkowanie analityczne funkcji momentów.
Zgodnie z metodą Maxwella-Mohra wyznaczenie przemieszczenia u, sprowadza się do obliczenia całki, pod znakiem której występuje moment gnący spowodowany rzeczywistym obciążeniem zewnętrznym (Mg), oraz moment gnący jaki wywołałaby jednostkowa siła fikcyjna P=1 odpowiadająca szukanemu przemieszczeniu (\(M_1\)).
\[ u=\int_{0}^{l} \frac{M_{g} \cdot M_{1}}{E I} d x \] Całkowanie można przeprowadzić analitycznie lub graficznie. W poniższym przykładzie pokażemy obydwa podejścia.
Zobacz całkowanie graficzne - metoda Wereszczagina
- jak wyznaczyć funkcje momentów gnących w przedziałach,
- jak określić stan jednostkowy i wyznaczyć funkcje momentów,
- jak przecałkować analitycznie iloczyny funkcji momentów na przedziałach,
- jak obliczyć ugięcie i kąt obrotu belki w dowolnym punkcie.
Metoda Wereszczagina:
- jak wyznaczyć wykresy momentów w stanie początkowym i jednostkowym,
- jak przecałkować graficznie wykresy momentów,
- jak obliczyć ugięcie i kąt obrotu belki w dowolnym punkcie.
Metoda Maxwella-Mohra - podejście uproszczone
(uwzględnienie tylko wpływu momentu gnącego)
Metoda Maxwella-Mohra jest kolejną ważną techniką energetyczną używaną do analizy przemieszczeń w konstrukcjach. Jest to metoda bardziej ogólna, która obejmuje zarówno obciążenia mechaniczne, jak i termiczne, geometryczne oraz podpory sprężyste. Wzór Maxwella-Mohra uwzględnia wpływ wszystkich możliwych oddziaływań na konstrukcję. W tej metodzie przemieszczenia od obciążeń mechanicznych oblicza się poprzez całkowanie iloczynów funkcji momentów zginających, sił tnących i sił normalnych dla stanów początkowych i jednostkowych.W tym podstawowym kursie zajmiemy się tylko wpływem momentów na przemieszczenie od obciążeń mechanicznych. Ponadto chcemy tutaj pokazać podejście podstawowe, w którym będziemy wykonywać całkowanie analityczne funkcji momentów.
Zgodnie z metodą Maxwella-Mohra wyznaczenie przemieszczenia u, sprowadza się do obliczenia całki, pod znakiem której występuje moment gnący spowodowany rzeczywistym obciążeniem zewnętrznym (Mg), oraz moment gnący jaki wywołałaby jednostkowa siła fikcyjna P=1 odpowiadająca szukanemu przemieszczeniu (\(M_1\)).
\[ u=\int_{0}^{l} \frac{M_{g} \cdot M_{1}}{E I} d x \] Całkowanie można przeprowadzić analitycznie lub graficznie. W poniższym przykładzie pokażemy obydwa podejścia.
Zobacz całkowanie graficzne - metoda Wereszczagina
Z tego kursu dowiesz się
Metoda Maxwella-Mohra (całkowanie analityczne funkcji momentów):- jak wyznaczyć funkcje momentów gnących w przedziałach,
- jak określić stan jednostkowy i wyznaczyć funkcje momentów,
- jak przecałkować analitycznie iloczyny funkcji momentów na przedziałach,
- jak obliczyć ugięcie i kąt obrotu belki w dowolnym punkcie.
Metoda Wereszczagina:
- jak wyznaczyć wykresy momentów w stanie początkowym i jednostkowym,
- jak przecałkować graficznie wykresy momentów,
- jak obliczyć ugięcie i kąt obrotu belki w dowolnym punkcie.
Przykład 1
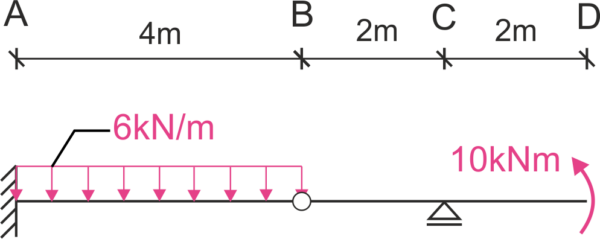
Treść
Oblicz przemieszczenie pionowe punktu D.
Uwzględnij wpływ momentów zginających.
Uwzględnij wpływ momentów zginających.
Rozwiązanie
Rozbijamy belkę przegubową na belki proste, liczymy reakcje bierne i rysujemy wykresy sił wewnętrznych. Uwaga – reakcje można policzyć bez rozbijania na belki proste. Sprawdzanie ekstremum nie jest potrzebne do policzenia przemieszczenia.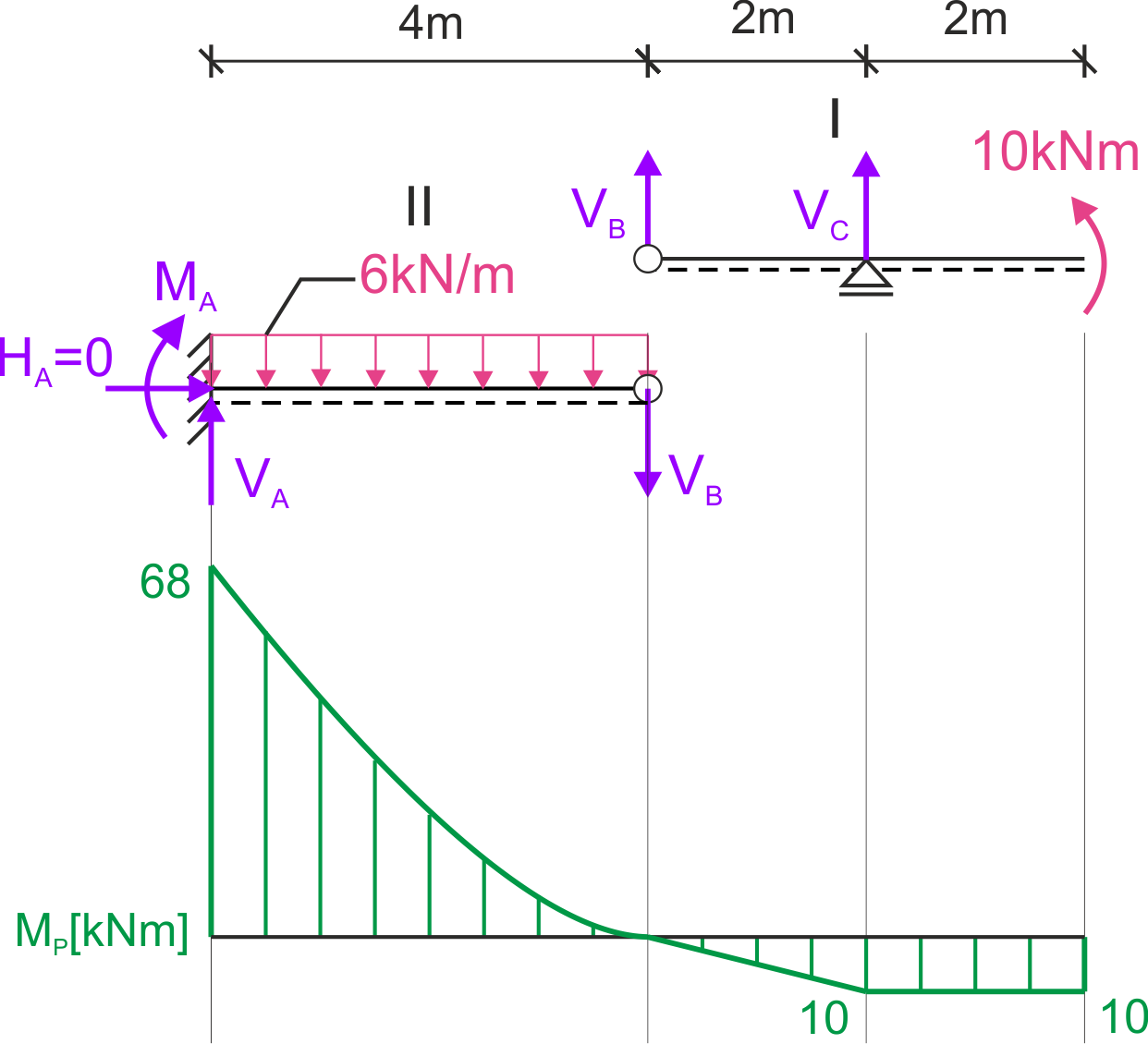
Reakcje podporowe
I
\begin{aligned} & \Sigma M_{B}=0 \\ & 10+2 V_{C}=0 \\ & V_{C}=-5 \mathrm{kN} \\ & \Sigma Y=0\\ & V_{B}+V_{C}=0 \\ & V_{B}=5 \mathrm{kN} \end{aligned}II
\begin{aligned} & \Sigma M_{A}=0 \\ & -M_{A}-6 \cdot 4 \cdot 2-4 V_{B}=0 \\ & M_{A}=-68 \mathrm{kNm} \\ & \Sigma Y=0 \\ & V_{A}-6 \cdot 4-V_{B}=0 \\ & V_{A}=29 \mathrm{kN} \end{aligned}Funkcje momentów zginających - stan początkowy
\begin{aligned} & \text{AB} \quad 0 < x < 4 \\ & M_1(x) = -68 + 29 \cdot x - 6 \cdot \frac{x^2}{2} \\ & \quad M_1(0) = -68 \, \text{kNm} \\ & \quad M_1(4) = 0 \, \text{kNm} \\ \\ & \text{BC} \quad 4 < x < 6 \\ & M_2(x) = -68 + 29 \cdot x - 6 \cdot 4 \cdot (x - 2) \\ & \quad M_2(4) = 0 \, \text{kNm} \\ & \quad M_2(6) = 10 \, \text{kNm} \\ \\ & \text{DC} \quad 0 < x < 2 \\ & M_3(x) = 10 \\ & \quad M_3(0) = 10 \, \text{kNm} \\ & \quad M_3(2) = 10 \, \text{kNm} \end{aligned}Stan jednostkowy
W celu obliczenia pionowego przemieszczenia w punkcie D przykładamy pionową siłę jednostkową i rysujemy wykres momentów.
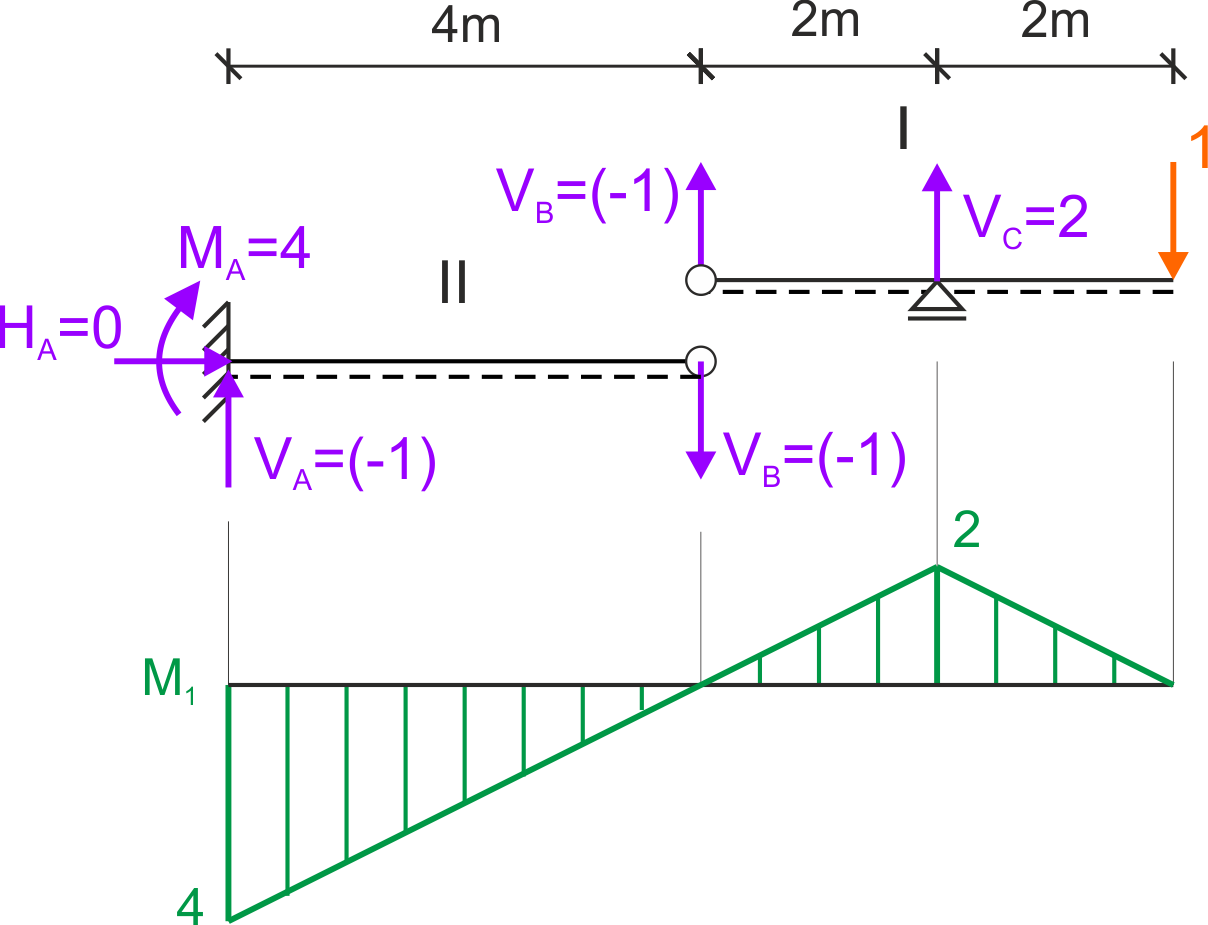
Reakcje podporowe
\begin{aligned} \text { I } & \\ & \Sigma M_{B}=0 \\ & -1 \cdot 4+2 V_{C}=0 \\ & V_{C}=2\\ & \Sigma Y=0 \\ & V_{B}+V_{C}-1=0 \\ & V_{B}=-1 \end{aligned} \begin{aligned} \text { II } & \\ & \Sigma M_{A}=0 \\ & -M_{A}-4 V_{B}=0 \\ & M_{A}=\frac{4}{m} \\ & \Sigma Y=0 \\ & V_{A}-V_{B}=0 \\ & V_{A}=-1 \end{aligned}Funkcje momentów zginających - stan jednostkowy
\begin{aligned} & \mathrm{AB} \quad 0<\mathrm{x}<4 \\ & \mathrm{~m}_1(\mathrm{x})=4-1 \cdot \mathrm{x} \quad \quad \mathrm{~m}_1(0)=4 \mathrm{~m} \quad \quad \mathrm{~m}_1(4)=0 \mathrm{~m}\\ \\ & \mathrm{BC} \quad 4<\mathrm{x}<6 \\ & \mathrm{~m}_2(\mathrm{x})=4-1 \cdot \mathrm{x} \quad \quad \mathrm{~m}_2(4)=0 \mathrm{~m} \quad \quad \mathrm{~m}_2(6)=-2 \mathrm{~m}\\ \\ & \text { DC } \quad 0<\mathrm{x}<2 \\ & \mathrm{~m}_3(\mathrm{x})=-1 \cdot \mathrm{x} \quad \quad \mathrm{~m}_3(0)=0 \quad \quad \mathrm{~m}_3(2)=-2 \mathrm{~m} \end{aligned}Obliczenie przemieszczenia - całkowanie analityczne
Wzór ogólny
\[ \Delta_{\mathrm{D}}=\int_0^4 \frac{\mathrm{M}_1(\mathrm{x}) \cdot \mathrm{m}_1(\mathrm{x})}{E I} \mathrm{dx}+\int_4^6 \frac{\mathrm{M}_2(\mathrm{x}) \cdot \mathrm{m}_2(\mathrm{x})}{E I} \mathrm{dx}+\int_0^2 \frac{\mathrm{M}_3(\mathrm{x}) \cdot \mathrm{m}_3(\mathrm{x})}{E I} \mathrm{dx} \]Podstawienie funkcji
\begin{aligned} \Delta_{\mathrm{D}}= & \frac{1}{\mathrm{EI}} \cdot\left[\int_0^4\left(-68+29 \cdot \mathrm{x}-3 \cdot \mathrm{x}^2\right) \cdot(4-\mathrm{x}) \mathrm{dx}+ \\ + \int_4^6[-68+29 \cdot \mathrm{x}-24 \cdot(\mathrm{x}-2)] \cdot(4-\mathrm{x}) \mathrm{dx} + \cdot \int_0^2 10 \cdot(-\mathrm{x}) \mathrm{dx}\right] \end{aligned}Uproszczenie wyrażeń pod całkami
\[ \Delta_{\mathrm{D}}=\frac{1}{\mathrm{EI}} \cdot\left[\int_0^4\left(3 \cdot \mathrm{x}^3-41 \cdot \mathrm{x}^2+184 \cdot \mathrm{x}-272\right) \mathrm{dx}+\\ +\int_4^6\left(40 \cdot \mathrm{x}-5 \cdot \mathrm{x}^2-80\right) \mathrm{dx}+\int_0^2-10 \mathrm{xdx}\right] \]Rozwiązanie całkowania krok po kroku
\begin{aligned} & \int_0^4\left(3 x^3-41 x^2+184 x-272\right) d x+\int_4^6\left(40 x-5 x^2-80\right) d x+\int_0^2-10 x d x= \\ & {\left[\frac{3 x^4}{4}-\frac{41 x^3}{3}+92 x^2-272 x\right]_0^4+\left[20 x^2-\frac{5 x^3}{3}-80 x\right]_4^6+\left[-5 x^2\right]_0^2=} \\ & \left(\frac{3 \cdot 256}{4}-\frac{41 \cdot 64}{3}+92 \cdot 16-272 \cdot 4\right)+\left(\left(20 \cdot 36-\frac{5 \cdot 216}{3}-80 \cdot 6\right)-\left(20 \cdot 16-\frac{5 \cdot 64}{3}-80 \cdot 4\right)\right)+(-5 \cdot 4)= \\ & \left(192-\frac{2624}{3}+1472-1088\right)+\left((720-360-480)-\left(320-\frac{320}{3}-320\right)\right)-20= \\ & \left(\frac{576}{1}-\frac{2624}{3}\right)+\left(-120+\frac{320}{3}\right)-20= \\ & -\frac{896}{3}-\frac{40}{3}-20=-\frac{936}{3}-20=-312-20=-332 \end{aligned} \[ \Delta_{\mathrm{D}}=\frac{-332}{\mathrm{EI}} \]To że przemieszczenie wyszło ujemne oznacza, że wystąpi ono w stronę przeciwną niż przyjęliśmy siłę jednostkową.
Obliczenie przemieszczenia - całkowanie graficzne
Dobrze będzie widać na tym przykładzie przewagę całkowania graficznego nad analitycznym przy liczeniu przemieszczeń.
\begin{aligned} & \Delta_{D}=\sum \int \frac{M_{P} M_{1}}{E I} d x\\ \end{aligned}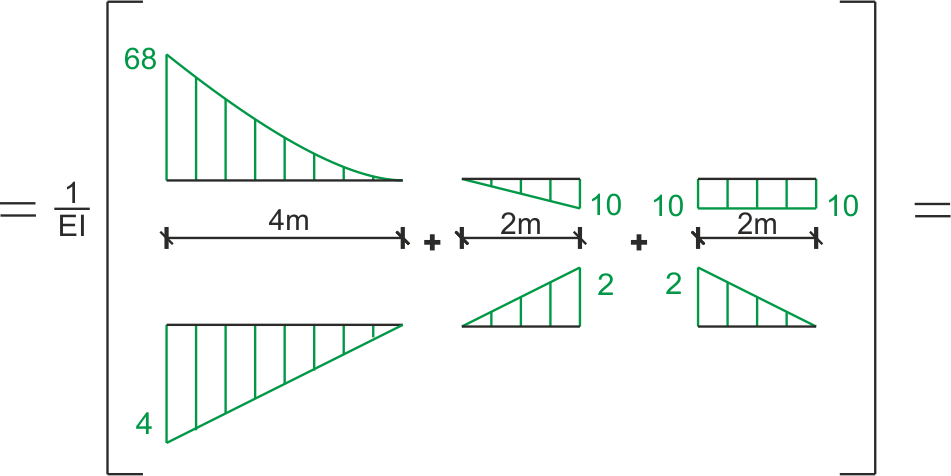
Rozkład paraboli na figury proste
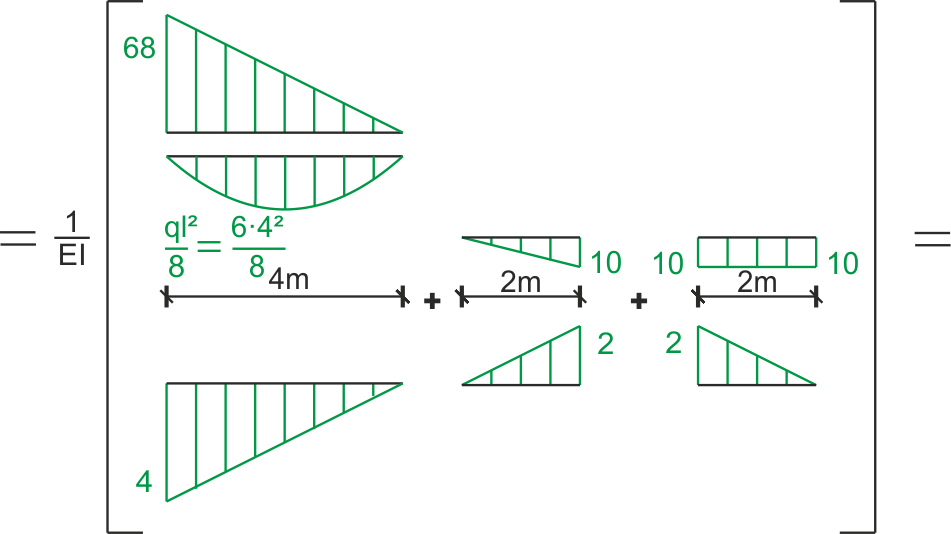
Jeżeli obydwa wykresy są po tej samej stronie pręta - wynik całkowania danej sekcji jest dodatni, jeśli po przeciwnych stronach pręta - wynik ujemny. Można umownie przyjąć, że na dole mamy moment dodatnie, u góry ujemne.
\begin{aligned} & \Delta_{D}=\sum \int \frac{M_{P} M_{1}}{E I} d x\\ & = \frac{1}{E I}\left[-\frac{1}{3} \cdot 4 \cdot 68 \cdot 4+\frac{1}{3} \cdot 4 \cdot 4 \cdot \frac{6 \cdot 4^{2}}{8}-\frac{1}{3} \cdot 2 \cdot 2 \cdot 10-\frac{1}{2} \cdot 2 \cdot 2 \cdot 10\right]=-332 \frac{1}{E I}\\ \end{aligned} Więcej informacji na temat całkowania graficznego znajdziecie tutaj - metoda WereszczaginaZOBACZ TEŻ

