Metoda Cremony

Z tego tekstu dowiesz się więcej na temat graficznej Metody Cremony obliczania sił w prętach kratownicy oraz znajdziesz przykłady rozwiązania kratownic z wykorzystaniem tej metody.

Metoda graficzna Cremony (plan sił Cremony) to technika stosowana do analizy sił wewnętrznych w prętach kratownic, szczególnie przydatna do rozwiązywania statycznie wyznaczalnych kratownic.

Warunek konieczny statycznej wyznaczalności

Zanim więc zagłębimy się w szczegóły tej metody, wyjaśnijmy sobie jak sprawdzić warunek konieczny statycznej wyznaczalności kratownicy.

p=2w-3

Dla sił zbiegających się w jednym węźle możemy zapisać dwa równania równowagi:
( \( \sum x=0 , \sum y=0 \) ). Oznaczając liczbę węzłów przez w, liczba wszystkich równań równowagi dla całej kratownicy wynosi 2w.
Trzy z tych równań wykorzystuje się do wyznaczenia reakcji w punktach podparcia, co oznacza, że do obliczenia sił w prętach pozostaje 2w−3 równań.
Aby równania statyki wystarczyły do rozwiązania kratownicy, czyli aby kratownica była statycznie wyznaczalna liczba sił wewnętrznych, które chcemy wyznaczyć, musi być równa 2w−3. Ponieważ liczba sił wewnętrznych jest równa liczbie prętów w kratownicy, oznaczając liczbę prętów przez p, otrzymujemy zależność przedstawioną dużymi literami powyżej.

Na czym bazuje metoda Cremony

Rozwiązanie kratownicy polega na wyznaczeniu reakcji podporowych w miejscach podparcia oraz sił wewnętrznych, które mogą działać w prętach w formie ściskania lub rozciągania.
Każdy węzeł kratownicy można rozpatrywać jako punkt, w którym zbiega się określona liczba sił zewnętrznych i wewnętrznych (siły czynne - przyłożone zewnętrznie, reakcje podporowe, siły w prętach).

W przypadku układu płaskiego mamy dwa rodzaje warunków równowagi:
• Analityczny – suma rzutów wszystkich sił na osie x i y musi być równa zeru.
• Graficzny – wielobok sił występujących w układzie musi się zamykać.

Na warunku graficznym bazuje metoda Cremony.

Główne założenia i kroki metody Cremony

Żeby prościej było zrozumieć kolejne kroki odnieśmy się do jakiegoś przykładu, weźmy na tapet taką kratownicę:

Rys1. Kratownica – temat zadania.

Oczywiście, sprawdzamy warunek konieczny statycznej wyznaczalności. Czy p=2w-3?
p = 9 – liczba prętów,
w = 6 – liczba węzłów,
a więc:
9 = 2 * 6 - 3
9 = 9 -> warunek spełniony.
Poza tym kratownica musi być również geometrycznie niezmienna, jednak nie będziemy teraz zagłębiać się w to zagadnienie.

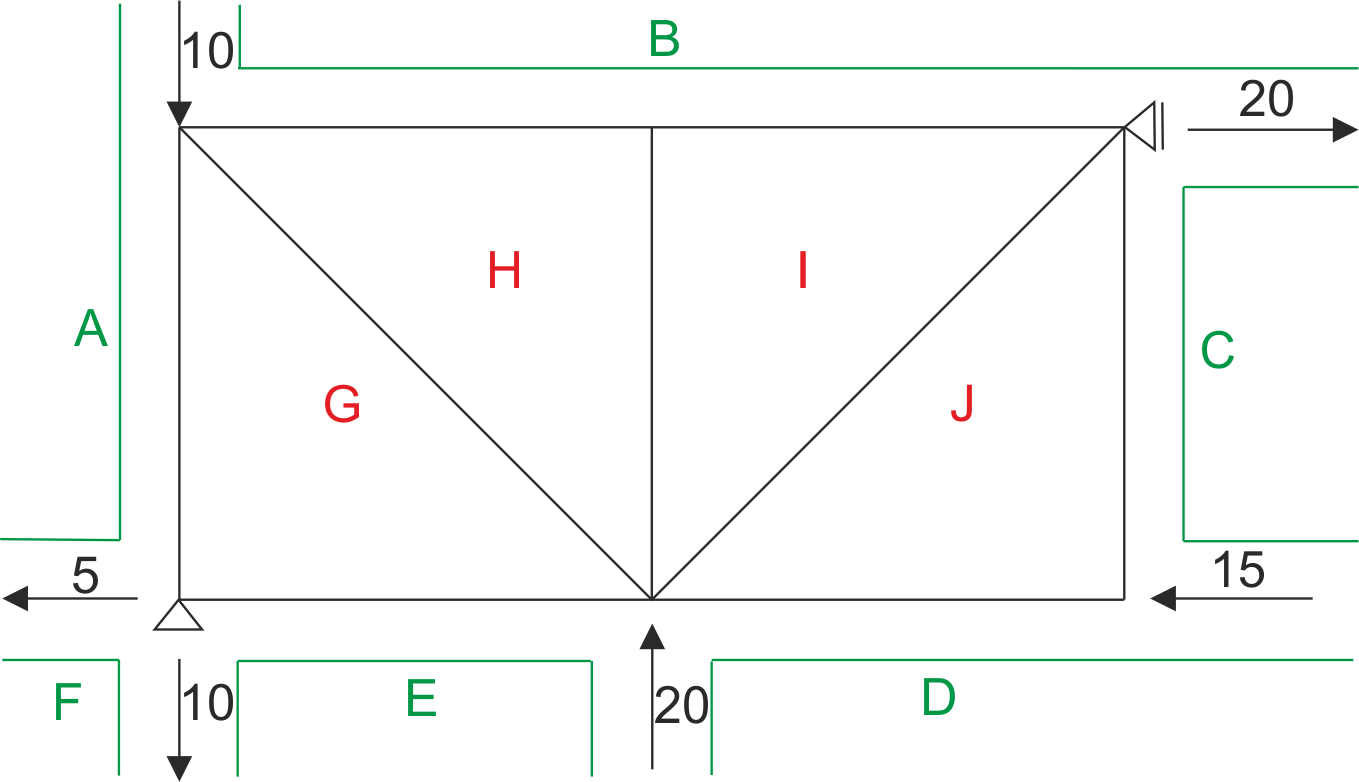
1. Rysunek konstrukcji i oznaczenie sił zewnętrznych

Zaczynamy od narysowania kratownicy, oznaczając siły zewnętrzne (obciążenia i reakcje podporowe). Każdy pręt w kratownicy powinien być oznaczony symbolami, aby łatwiej było odnosić się do niego podczas analizy.

Rys2. Oznaczenie węzłów, prętów kratownicy, reakcji podporowych.

2. Obliczenie reakcji podporowych

Z warunków statyki:
\( \sum x = 0,\quad \sum y = 0,\quad \sum M = 0 \)
Na podstawie tych równań obliczamy reakcje podporowe.

Dla rozpatrywanego przykładu:

Reakcje

\begin{aligned} &\sum{M_A}=0 &-20\cdot 4+H_B\cdot 4-0 && H_B=20 \ kN\\ &\sum{X}=0 & M_A+H_B-15=0 && H_A=-5 \ kN\\ &\sum{Y}=0 & V_A-10+20=0 && V_A=-10 \ kN\\ \end{aligned}

3. Opisanie zewnętrznych i wewnętrznych pól kratownicy

Opisujemy (np. A, B, C itd.) pola kratownicy zewnętrzne, które oddzielają siły bierne (reakcje) oraz siły czynne – przyłożone z zewnątrz, a także pola kratownicy wewnętrzne. Nie ma znaczenia, gdzie umieścimy pole „A”.

Rys3. Opisanie zewnętrznych i wewnętrznych pól kratownicy.

4. Tworzenie zewnętrznego wieloboku sił

Tworzymy wielobok sił składający się z sił zewnętrznych. Sprawdzamy, czy wielobok sił się zamyka. Przechodzimy od pola A do pola B, C itd.

1) Idąc z pola A do pola B, zaznaczamy wektor między tymi polami, czyli 10 kN w wybranej skali. Początek tego wektora opisujemy jako punkt A, a koniec jako punkt B.
2) Następnie między polem B i C mamy wektor 20 kN. Początek wektora w punkcie B, a zwrot do punktu C.
3) Zaznaczamy wektor 15 kN z punktu C do punktu D.
4) Wektor 20 kN z punktu D do E.
5) Wektor 10 kN w dół, z punktu E do F.
6) Wektor 5 kN w lewo, który domyka wielobok sił – z punktu F wracamy do punktu A. SUKCES!

Wideo1. Rysowanie wieloboku sił zewnętrznych.

5. Tworzenie wewnętrznych wieloboków sił dla kolejnych węzłów

Dla kolejnych węzłów tworzymy tzw. wielobok sił (wykres wektorowy). Zaczynamy od węzła, gdzie znane są siły zewnętrzne lub reakcje podporowe, a niewiadome są siły tylko w dwóch prętach które dochodzą do tego węzła.

Rysujemy siły w skali, w odpowiednich kierunkach. Powstaje wielobok, którego kolejne odcinki odpowiadają siłom działającym w prętach kratownicy. Kontynuujemy budowanie wykresu sił dla kolejnych węzłów, aż wszystkie siły w kratownicy zostaną wyznaczone.

Siły w prętach są proporcjonalne do długości odcinków na wykresie sił Cremony. Na podstawie tego wykresu możesz określić, które pręty są ściskane, a które rozciągane. Decyduje o tym zwrot w którym musieliśmy się poruszyć aby przejść z jednego pola do drugiego, jeśli zwrot jest „do węzła”, to pręt jest ściskany, jeśli „od węzła” to pręt jest rozciągany.

6. Rysowanie wykresu sił osiowych (normalnych)

Najlepiej po stworzeniu wieloboku dla każdego węzła od razu rysować wykres sił osiowych na kratownicy.

Ciężko to zrozumieć bez przykładu, a więc na przykładzie wygląda to tak:

Bazą do budowania równowagi kolejnych węzłów jest zewnętrzny wielobok sił który mamy już narysowany. Są tylko dwa węzły od których możemy zacząć analizę kratownicy, tzn. tylko w dwóch węzłach jest nie więcej niż dwie niewiadome siły w prętach. Jest to węzeł na dole po lewej i po prawej stronie, na pierwszym rysunku oznaczone jako A i F.

Zacznijmy od węzła na dole po lewej stronie

Przechodzimy przez kolejne pola konstruując wielobok sił, poruszajmy się zgodnie z ruchem wskazówek zegara przechodząc między polami.
1) Między polem A i G mamy pręt, którego kierunek jest pionowy, możemy zaznaczyć więc przerywaną linię/jasno szarą z punktu A o kierunku pionowym i gdzieś na tej lini musi znajdować się punkt G.
2) Między polem G i E mamy kierunek poziomy, możemy więc z punktu E, który wiemy gdzie jest, zaznaczyć kierunek poziomy i tym oto sposobem znajdujemy punkt G.
3) Rysujemy wektory z A do G, z G do E, długości tych wektorów to w przyjętej skali wartości sił w prętach, a zwrot z jakim się poruszyliśmy obchodząc ten węzeł pokazuje nam czy pręt jest rozciągany czy ściskany.
4) Zaznaczamy obliczone (znalezione graficznie właściwie) siły na wykresie.

Wideo2. Rysowanie wieloboku sił wewnętrznych – węzeł pierwszy.

Oba pręty są rozciągane.

Kolejny będzie węzeł po lewej stronie u góry

Znamy już siłę w pręcie pionowym, niewiadome są siły w pręcie skośnym i poziomym, a więc możemy analizować ten węzeł.
1) Z pola B do H zaznaczamy poziomy kierunek, wiemy gdzie jest punkt B, szukamy punktu H.
2) Z pola H do G zaznaczamy kierunek pod kątem pod którym jest pręt skośny między tymi polami, z poprzedniego kroku wiemy gdzie jest punkt G, więc przez ten punkt przechodzi na prosta i tak oto znajdujemy punkt H.
3) Rysujemy wektory z B do H i z H do G, długości tych wektorów to w przyjętej skali wartości sił w prętach, a zwrot z jakim się poruszyliśmy obchodząc ten węzeł pokazuje nam czy pręt jest rozciągany czy ściskany.
4) Zaznaczamy obliczone (znalezione graficznie właściwie) siły na wykresie.

Wideo3. Rysowanie wieloboku sił wewnętrznych – węzeł drugi.

I tak dalej przechodzimy przez kolejne węzły aż wyznaczymy siły we wszystkich prętach.
Tak powinien wyglądać kompletny wykres:

Wykres sił normalnych [kN]

Rys4. Wykres sił normalnych [kN].

Podsumowując, metoda Cremony jest narzędziem graficznym stosowanym głównie w analizie sił w statycznie wyznaczalnych kratownicach. Polega na tworzeniu wykresów sił dla każdego węzła, co pozwala określić siły działające w prętach.