Metoda Clebscha
- E - moduł Younga,
- J - moment bezwładności przekroju belki względem osi poziomej.
Znak „-"po prawej stronie równania wynika z przyjętego układu współrzędnych
i umowy określającej znak momentu gnącego.
W celu wyznaczenia ugięć belki całkujemy dwukrotnie powyższe równanie
i otrzymujemy pierwszą pochodną - funkcję kąta obrotu belki
oraz drugą pochodną - funkcje ugięcia
C i D oznaczają stałe całkowania.
Stałe całkowania wyznaczamy z kinematycznych warunków brzegowych, tj. warunków na zerowe ugięcia i kąty ugięć w określonym typie podpory. Zobacz jakie są rodzaje podpór dla belki na płaszczyźnie
Tak jak zauważyliśmy metoda Clebscha, przy zachowaniu pewnych warunków sposobu zapisu, pozwala dla belki prostej otrzymać równanie linii ugięcia zawierające tylko dwie niewiadome (stałe całkowania) niezależnie od liczby przedziałów.
Zasady regulujące stosowanie metody Clebscha można ująć w 4 punktach:
- odcięte we wszystkich przedziałach muszą być mierzone od tego samego punktu
przyjmujemy dla belki prostej jeden układ współrzędnych, nie możemy zapisać np. części funkcji od jednej, a części od drugiej strony belki
- w przypadku działania obciążenia ciągłego nie może ono ulec przerwaniu
o ile taki przypadek zachodzi, to obciążenie ciągłe należy przedłużyć do końca belki, dodając jednocześnie takie samo obciążenie, ze znakiem przeciwnym (kontr-obciążenie)
- wszystkie nowo dochodzące człony w wyrażeniu na moment gnący muszą zawierać czynnik \( (x- l_{i-1}) \),
gdzie:
\(l_{i-1}\) oznacza współrzędną początku i-tego przedziału belki
- w przypadku pojawienia się momentu skupionego M – domnażamy moment przez ramię działania do potęgi 0
- całkowanie należy wykonać bez rozwijania wyrażeń w nawiasach
stałe całkowania obowiązują dla całej belki (dla wszystkich przedziałów)
Jeśli współrzędne \(l_{\mathrm{i}}\) określają położenie sił skupionych \(P_{\mathrm{i}}\)
lub początków obciążenia ciągłego \(q_{\mathrm{i}}\),
to wyrażenia typu \(P_i\left(x-l_i\right)\) lub \(q_i \frac{\left(x-l_i\right)^2}{2}\) całkuje się według schematu
A teraz spójrzmy na przykład poniżej i zobaczmy rozwiązanie w praktyce.
Zobacz przykład
Belka trzyprzedziałowa z różnymi rodzajami obciążeń.
Obliczyć ugięcie i kąt obrotu w zadanym punkcie belki.
Rozwiązanie przykładu z wideo-kursu
Treść
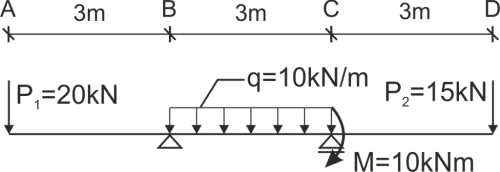
Rozwiązanie
Obliczamy reakcje podporowe
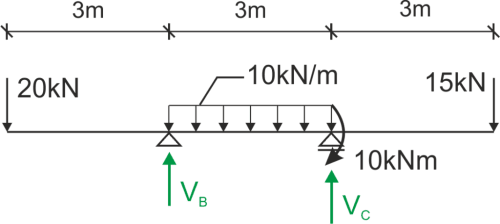\begin{aligned} &\sum{M_B}=0 -20\cdot 3+30\cdot 1.5+10+15\cdot 6-R_C\cdot 3=0 R_A=28.33kN\\ &\sum{M_C}=0 -20\cdot 6+R_B\cdot 3-30\cdot 1.5+10+15\cdot 3=0 R_B=36.67kN\\ &\sum{P_iY}=0 -20+R_B-30+R_C-15=0 L=P\\ \end{aligned}
Zapisujemy funkcję momentu od lewej strony.
Funkcję można też zapisać z prawej strony. Zachęcamy do sprawdzenia tego wariantu, obliczenia szukanego przemieszczenia i porównania wyników.
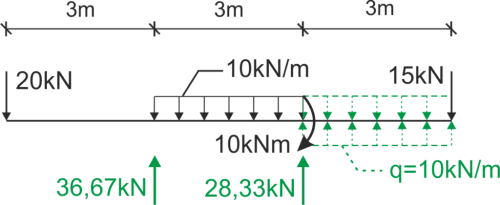\begin{aligned}
&M_g(x)=-20x+R_B(x-3)-\frac{1}{2}q(x-3)^2+R_C(x-6)+10(x-6)^0+\frac{1}{2}q(x-6)^2\\
&EJ\cdot w"=-M_g(x)=20x-R_B(x-3)+5(x-3)^2- 28.33(x-6)-10(x-6)^0-5(x-6)^2\\
&EJ\cdot w'=20\frac{x^2}{2}-36.67\frac{(x-3)^2}{2}+5\frac{(x-3)^3}{3}-28.33\frac{(x-6)^2}{2}-10(x-6)-5\frac{(x-6)^3}{3}+C\\
&EJ\cdot w=20\frac{x^3}{6}-36.67\frac{(x-3)^3}{6}+5\frac{(x-3)^4}{12}-28.33\frac{(x-6)^3}{6}-10\frac{(x-6)^2}{2}-5\frac{(x-6)^4}{12}+Cx+D\\
\end{aligned}
Warunki brzegowe
\begin{aligned} &w(x=3)=0 \Rightarrow 90+3C+D=0\\ &w(x=6)=0 \Rightarrow 588.735+6C+D=0\\ &C=-166,245\\ &D=408.735\\ \end{aligned}Obliczamy ugięcie w punkcie A.
Jeśli układ współrzędnych przyjęliśmy na lewym końcu belki, to punkt A ma współrzędną x=0.
Wobec tego \begin{aligned} &w_A(x=0)=\frac{1}{EI}\cdot (D)\\ \end{aligned} \begin{aligned} &w_A=\frac{1}{EI}\cdot (408.735)\\ \end{aligned}
ZOBACZ TEŻ
Teoria
Zadania
Nagrania
