Łuki paraboliczne

Zastosowanie łuków parabolicznych

Łuki paraboliczne są cenione w budownictwie nie tylko za swoją funkcjonalność, ale także za estetyczny wygląd. Ze względu na zdolność do efektywnego przenoszenia obciążeń, są wybierane tam, gdzie liczy się lekka i wytrzymała konstrukcja, zwłaszcza w projektach dużych, otwartych przestrzeni. Dzięki swojej geometrii, łuki paraboliczne są w stanie równomiernie rozkładać obciążenia i są bardziej wytrzymałe niż łuki kołowe przy takich samych warunkach.
Oto niektóre miejsca, w których można je spotkać:

• Mosty i wiadukty: Charakterystyczna forma łuku parabolicznego czyni je idealnymi do przekraczania rozpiętości rzek, dolin czy innych przeszkód terenowych.
• Kościoły i budynki sakralne: Łuki paraboliczne odgrywają ważną rolę w architekturze sakralnej, gdzie są wykorzystywane do budowy kopuł, sklepień i arkad. Ich elegancka forma nie tylko zapewnia wytrzymałość, ale także nadaje wnętrzom wyjątkowy charakter.
• Dachy i hale: Łuki paraboliczne stosuje się w konstrukcji dużych dachów nad halami, magazynami czy hangarami, gdzie pozwalają uzyskać duże rozpiętości bez konieczności użycia licznych podpór.
• Tunele i galerie: W budownictwie podziemnym łuki paraboliczne są wykorzystywane jako elementy konstrukcyjne w tunelach i galeriach.
• Stadiony i obiekty sportowe: Konstrukcje dachów na stadionach często opierają się na łukach parabolicznych, które zapewniają lekkość konstrukcji i możliwość zadaszenia dużych obszarów bez podpór wewnętrznych.

Siły wewnętrzne w łukach parabolicznych

Reakcje podporowe dla łuków liczy się tak samo jak dla belek, ram, czy kratownic.
Największą trudnością przy obliczaniu sił wewnętrznych jest krzywoliniowy kształt pręta. Jednak z pomocą przychodzi nam trygonometria, która pozwoli nam obliczyć siły normalne i tnące. Pamiętajmy, że siły tnące i normalne będą zmieniać swoje kierunki wzdłuż krzywoliniowej linii łuku.

Funkcje sił wewnętrznych

Aby rozjaśnić kluczowe elementy analizy sił wewnętrznych w łukach parabolicznych rozważmy częściowo poniższy przykład: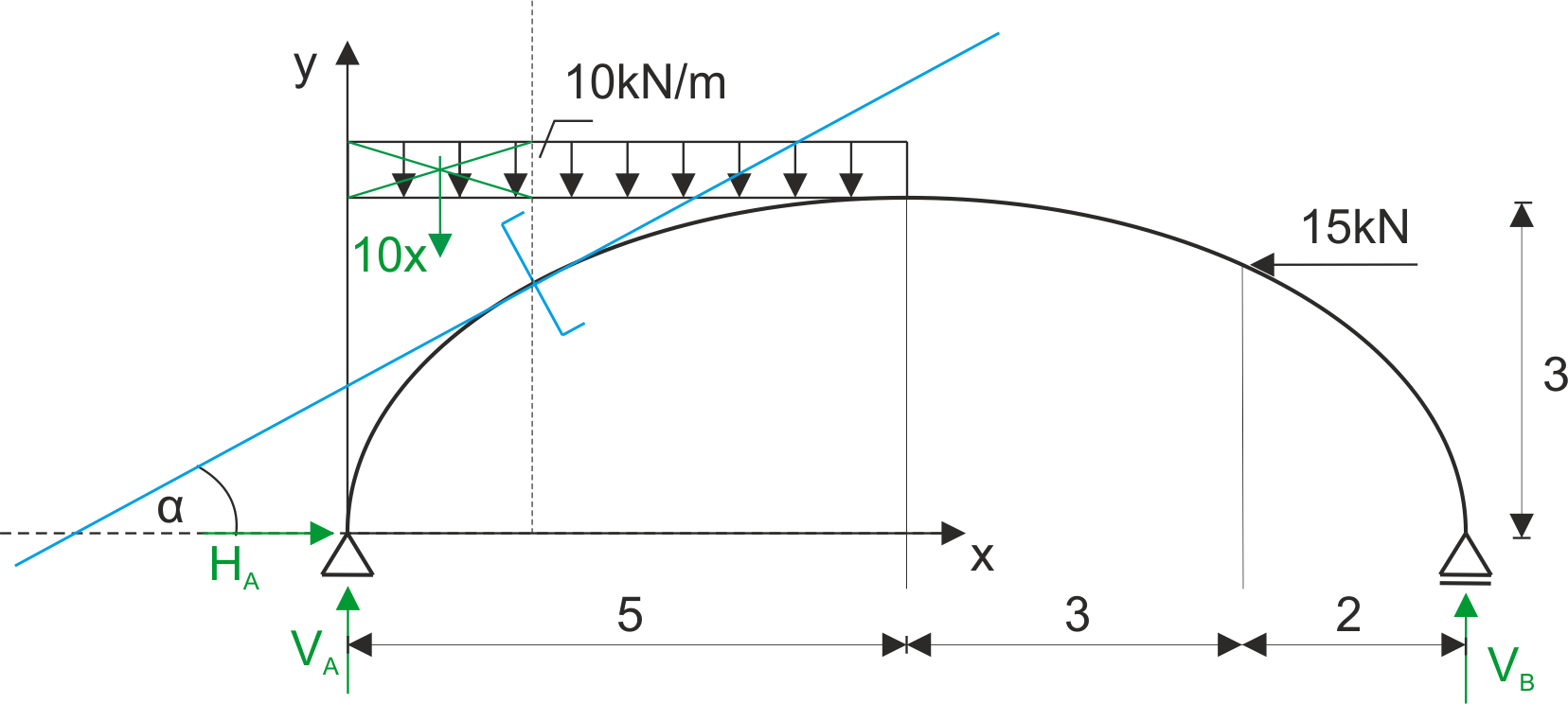

Rys1. Przekrój myślowy dla łuku parabolicznego

Dla łuków parabolicznych inaczej niż dla łuków kołowych przyjmuje się układ współrzędnych na lewym albo prawym końcu.
Aby wyznaczyć współrzędną pionową punktu przyłożenia siły, a także żeby obliczyć \( tg \alpha \), \( sin \alpha \) i \( cos \alpha \) musimy najpierw wyznaczyć równanie łuku parabolicznego (równanie paraboli).
Pokażemy dwie metody.

Równanie osi łuku parabolicznego

Metoda l

Znamy 3 punkty które należą do łuku - podpora A, B oraz wierzchołek - podstawiamy je do równania paraboli, rozwiązujemy układ równań i wyznaczamy parametry funkcji kwadratowej.
Równanie paraboli \(\mathrm{y}=\mathrm{a} \cdot \mathrm{x}^2+\mathrm{b} \cdot \mathrm{x}+\mathrm{c}\)
Współrzędne punktów:
\( \mathrm{A}(0,0), \mathrm{B}(10,0), \mathrm{W}(5,3) \)

Wstawiamy do równania
punkt A:
\(0=\mathrm{a} \cdot 0^2+\mathrm{b} \cdot 0+\mathrm{c}\)
c=0

punkt B : \begin{aligned} & 0=\mathrm{a} \cdot 10^2+\mathrm{b} \cdot 10+\mathrm{c} \\ & \mathrm{~b}=-10 \mathrm{a} \end{aligned} punkt C:
\( 3=\mathrm{a} \cdot 5^2+\mathrm{b} \cdot 5+\mathrm{c}\)
\begin{aligned} & 3=a \cdot 5^2+(-10 a) \cdot 5 \\ & 3=-25 a \\ & a=\frac{-3}{25}=-0.12 \end{aligned} Wobec tego \( \quad b=-10 \mathrm{a}=1.2 \)
A więc funkcja paraboli: \(\mathrm{y}=-0.12 \cdot \mathrm{x}^2+1.2 \cdot \mathrm{x} \)

Metoda II

Skorzystanie z równania osi łuku parabolicznego, przy początku układu współrzędnych na podporze A: \( y=\frac{4 f}{L^2} \cdot(L-x) \cdot x\), gdzie:
\(f-\) wysokość łuku,
\(L-\) rozpiętość między podporami.
Mamy \(\mathrm{f}=3, \mathrm{~L}=10\), wobec tego:
\(\mathrm{y}=\frac{4 \cdot 3}{10^2} \cdot(10-\mathrm{x}) \cdot \mathrm{x}=0.12 \cdot(10-\mathrm{x}) \cdot \mathrm{x}=1.2 \mathrm{x}-0.12 \mathrm{x}^2\)

Znając równanie osi łuku parabolicznego możemy obliczyć pionową współrzędną przyłożenia siły.
dla \(\mathrm{x}=8 \mathrm{~m} \quad \mathrm{y}_{\mathrm{P}}=-0.12 \mathrm{x}^2+1.2 \mathrm{x}=1.92 \mathrm{~m}\)

Kierunek normalny i tnący

Robimy przekrój myślowy, puszczamy styczną do łuku przechodzącą przez ten punkt w którym zrobiliśmy przekrój (na rysunku powyżej na niebiesko). Ta styczna wyznacza kierunek normalny w tym przekroju myślowym. Prostopadle do kierunku normalnego jest kierunek tnący, Musimy zrzutować siły działające na ten przekrój od lewej strony na kierunek normalny i tnący.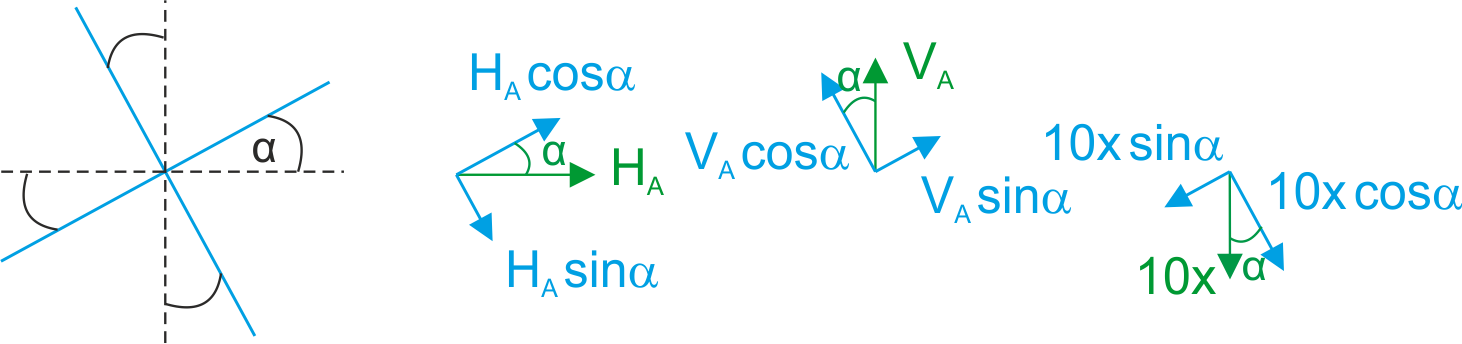

Rys2. Rzutowanie sił na składowe normalne i tnące

Powtórka z matematyki - styczna do łuku jest nachylona do osi x pod kątem \( \alpha \), którego tangens
\(\operatorname{tg} \alpha=\frac{\partial y}{\partial x}\)
W rozważanym przykladzie
\( \operatorname{tg} \alpha=\frac{\left(-0.12 \mathrm{x}^2+1.2 \mathrm{x}\right)}{\mathrm{dx}}=-0.24 \cdot \mathrm{x}+1.2 \)
Z trygonometrii mamy zależności które pozwolą nam wyznaczyć sinus i cosinus tego kąta
\( \sin \alpha=\frac{\operatorname{tg} \alpha}{\sqrt{1+\operatorname{tg}^2 \alpha}} \quad, \quad \cos \alpha=\frac{1}{\sqrt{1+\operatorname{tg}^2 \alpha}} \)

Mając zrobione to wszystko funkcje sił wewnętrznych rozpisujemy klasycznie.

Zapraszamy do zgłębiania tematu i analizy sił wewnętrznych w łukach parabolicznych. Powodzenia! 🛠️🔍