Rezystancja zastępcza

Czasami zanim zaczniemy obliczać zadanie związane z obwodem elektrycznym można je uprościć poprzez zamianę kilku rezystorów (lub innnych elementów np. w przypadku analizy obwodów prądu przemiennego metodą symboliczną) na jeden który opisuje rezystancja (w przypadku analizy obwodów prądu przemiennego impedancja) zastępcza.

Istnieje szereg zadań w których obliczenie rezystancji zastępczej jest konieczne z innych powodów - porównaj na przykład Metoda Thevenina lub Metoda Nortona.

Połączenie szeregowe

Jeżeli elementy są połączone szeregowo:

1. Prąd płynący przez nie ma taką samą wartość
2. Rezystancja zastępcza jest sumą rezystancji poszczególnych elementów
\begin{aligned} &R_z=R_1+R_2+...\\ &R_z=\sum{R_i} \end{aligned}

Bardzo ważne jest zauważyć, że kluczowe dla określenia czy elementy są połączone szeregowe jest stwierdzenie czy płynie przez nie taki sam prąd, będzie to lepiej widoczne w przykładach

Połączenie równolegle

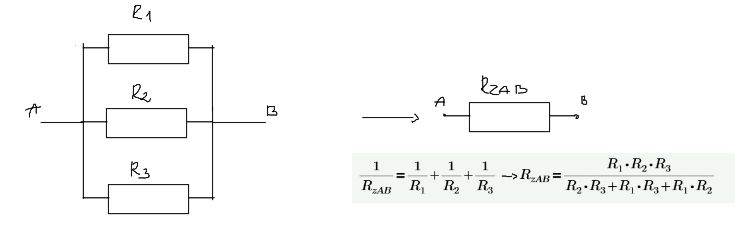
Jeżeli elementy są połączone równolegle:

1. Napięcie na nich ma taką samą wartość
2. Konduktancja zastępcza jest sumą konduktancji poszczególnych elementów
\begin{aligned} &G_z=G_1+G_2+...\\ &G_z=\sum{G_i} \end{aligned}
3. Odwrotność rezystancji zastępczej jest sumą odwrotności rezystancji poszczególnych elementów
\begin{aligned} &\frac{1}{R_z}=\frac{1}{R_1}+\frac{1}{R_2}+...\\ &\frac{1}{R_z}=\sum{\frac{1}{R_i}}\\ \end{aligned}

Bardzo ważne jest zauważyć, że kluczowe dla określenia czy elementy są połączone równolegle jest stwierdzenie czy występuje na nich takie samo napięcie

Dla jasności - bardzo rzadko jest naprawdę korzystnie użyć wzoru z konduktancją, ale pomaga on zobaczyć zależność która występuje dla takiego połączenia elementów

W praktyce warto też zapamiętać wzór dla dwóch elementów połaczonych równolegle:

\begin{aligned} &\frac{1}{R_z}=\frac{1}{R_1}+\frac{1}{R_2}=\frac{R_2}{R_1\cdot R_1 }+\frac{R_1}{R_2\cdot R_1 }\\ &\frac{1}{R_z}=\frac{R_1+R_2}{R_1\cdot R_2}\\ &R_z=\frac{R_1\cdot R_2}{R_1+R_2}\\ \end{aligned}

Jeżeli kiedykolwiek najdzie Cię wątpliwość co jest w mianowniku a co w liczniku pamiętaj że na koniec musi Ci wyjść poprawna jednostka - \(\Omega\), więc mnożenie MUSI być w liczniku ponieważ:

\begin{aligned} &\frac{\Omega\cdot \Omega}{\Omega + \Omega}=\frac{\Omega^2}{\Omega}=\Omega\\ \end{aligned}

a nie:

\begin{aligned} &\frac{\Omega+\Omega}{\Omega \cdot \Omega}=\frac{\Omega}{\Omega^2}=\frac{1}{\Omega}\\ \end{aligned}

Połączenie mieszane (szeregowo – równoległe)

Osobiście bardzo nie lubię tego określenia :-) W praktyce połączenie mieszane trzeba i tak sprowadzić do superpozycji połączeń szeregowych i równoległych więc nie widzę szczególnego powodu dla wyróżniania tego jako osobnego przypadku.

Natomiast w tym miejscu pozwolę sobie na małą dygresję - każda rezystencja zastępcza jest liczona względem dwóch punktów (zacisków), to nie jest jakaś wartość absolutna a jedynie uproszczenie które stosujemy żeby ułatwić sobie życie

Rezystancja zastępcza z praw Kirchhoffa

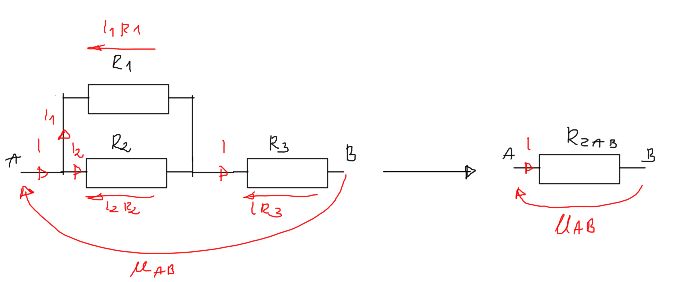
BARDZO przydatnym podejściem do myślenia o rezystancji zastępczej, szczególnie w bardziej skomplikowanych i nieoczywistych przypadkach które pojawiają się czasami np. w zadaniach z Metody Thevenina jest podejście do niej od strony praw Kirchoffa.

Wyobraźmy sobie na chwilę że pomiędzy zaciskami AB względem których mamy policzyć rezystancję zastępczą występuje napięcie \(U_{AB}\) które powoduje przepływ prądu \(I\)

Oczywistym jest, że \(R_z=\frac{U_{AB}}{I}\)

Dane:

\begin{aligned} R_1 & =30 \\ R_2 & =20 \\ R_3 & =10 \end{aligned}

Korzystając ze wzorów dla połączenia szeregowego i równoległego:

\begin{aligned} &R_{12}=\frac{R_1 \cdot R_2}{R_1+R_2}=12\\ &R_{z A B}=R_{12}+R_3=22 \end{aligned}

Korzystając z praw Kirchhoffa:

\begin{aligned} & I=I_1+I_2 \\ & I_1 \cdot R_1=I_2 \cdot R_2 \\ & U_{A B}=I_2 \cdot R_2+I \cdot R_3 \\ & R_{z A B}=\frac{U_{A B}}{I} \end{aligned}

Obliczamy:

\begin{aligned} & I_1=\frac{I_2 \cdot R_2}{R_1} \\ & I=\frac{I_2 \cdot R_2}{R_1}+I_2 \\ & I_2=\frac{R_1 \cdot I}{R_2+R_1} \\ & U_{A B}=\frac{R_1 \cdot I}{R_2+R_1} \cdot R_2+I \cdot R_3 \\ & R_{z A B}=\frac{\frac{R_1 \cdot I}{R_2+R_1} \cdot R_2+I \cdot R_3}{I}=\frac{R_1}{R_2+R_1} \cdot R_2+R_3=22 \end{aligned}

I jasne, że to nie jest de facto obliczanie rezystancji zastępczej, ale w bardziej złożonych przypadkach ten sposób myślenia potrafi bardzo pomóc chociaż same obliczenia z reguły będą bardziej skomplikowane