Przykład 1

Zad 3 W obwodzie jak na rysunku wyznaczyć napięcie na reaktancji pojemnościowej $$ \begin{aligned} E_{1}=10 \mathrm{~V} & E_{2}=10 \cdot e^{j 0^{\circ}} v & R_{1}=5 \Omega \quad R_{2}=5 \Omega \\ X_{L_{1}} &=X_{L_{2}}=10 \Omega \quad X_{c}=5 \Omega \quad X_{M}=\cap 0 \Omega \end{aligned} $$

single-task-hero-img

Rozwiązanie

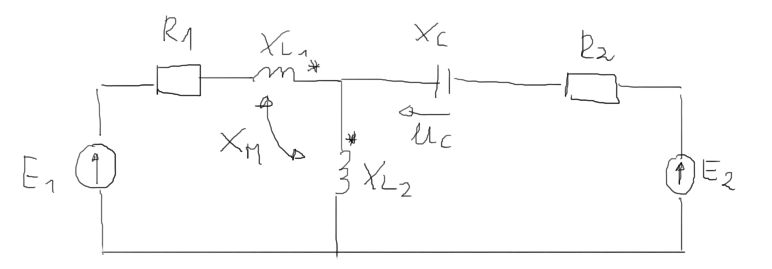
\begin{aligned} &E_{1}:=10 \\ &E_{2}:=10 \cdot e^{1 j \cdot 90 d e g}=10 \mathrm{i} \\ &R_{1}:=5 \\ &Z_{C}:=-5 \mathrm{j} \\ &R_{2}:=5 \\ &Z_{M}:=10 \mathrm{j} \\ &Z_{L 1}:=1 \mathrm{j} \cdot 10 \\ &Z_{L 2}:=1 \mathrm{j} \cdot 10 \end{aligned} Ponieważ $$ Z_{L 2}-Z_{M}=0 \quad->\quad z \text { warcie } $$ $$ \begin{aligned} &I_{1}:=\frac{E_{1}}{R_{1}+Z_{L 1}-Z_{M}}=2 \\ &I_{3}:=-\frac{E_{2}}{R_{2}+Z_{C}+Z_{M}}=-1-1 \mathrm{i} \\ &I_{1}-I_{2}-I_{3}=0 \\ &I_{2}:=I_{1}-I_{3}=3+1 \mathrm{i} \\ &U_{C}:=I_{3} \cdot Z_{C}=-5+5 \mathrm{i} \end{aligned} $$ sprawdzenie sprzeżenie nie-zgodne $$ \begin{aligned} &U_{L 1}:=I_{1} \cdot Z_{L 1}-I_{2} \cdot Z_{M}=10-10 \mathrm{i} \\ &U_{L 2}:=I_{2} \cdot Z_{L 2}-I_{1} \cdot Z_{M}=-10+10 \mathrm{i} \end{aligned} $$ $\begin{array}{lll}\text { oczko lewe } & E_{1}-I_{1} \cdot R_{1}-U_{L 1}-U_{L 2}=0 & O K \\ \text { oczko prawe } & U_{L 2}-U_{C}-I_{3} \cdot R_{2}-E_{2}=0 & O K\end{array}$