Lista zadań
Przykład 1
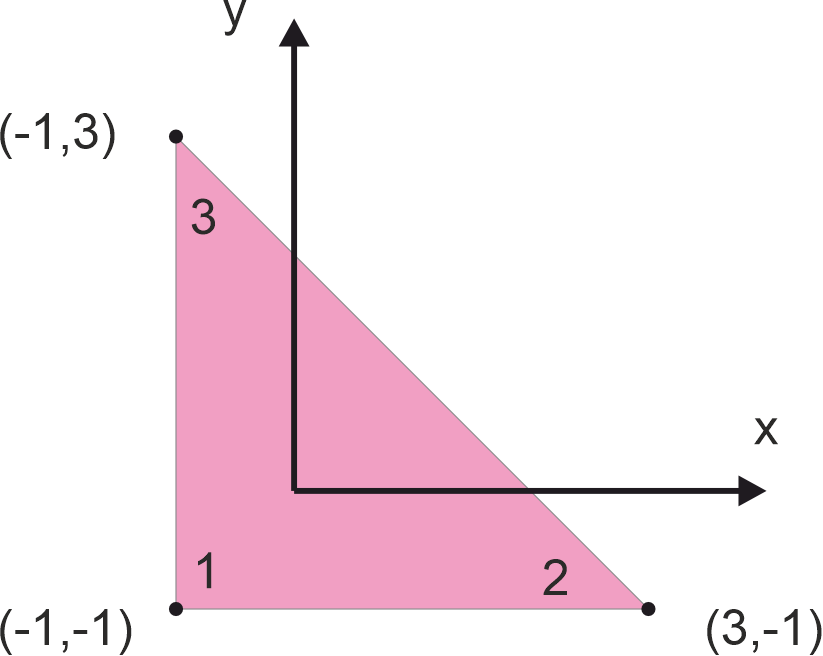
Dla danych jak na rysunku stosując procedurę MES policzyć wektor przemieszczeń w punkcie \(\mathrm{P}(0,1)\). \begin{aligned} & N_1(x, y)=\frac{1}{2}-\frac{x}{4}-\frac{y}{4} \\ & N_2(x, y)=\frac{1}{4}+\frac{x}{4} \\ & N_3(x, y)=\frac{1}{4}+\frac{y}{4} \\ & \mathrm{Q}^e=\{1,2,-0.5,-1,0.2,-0.4\} \cdot 10^{-4} \end{aligned}
Przykład 2
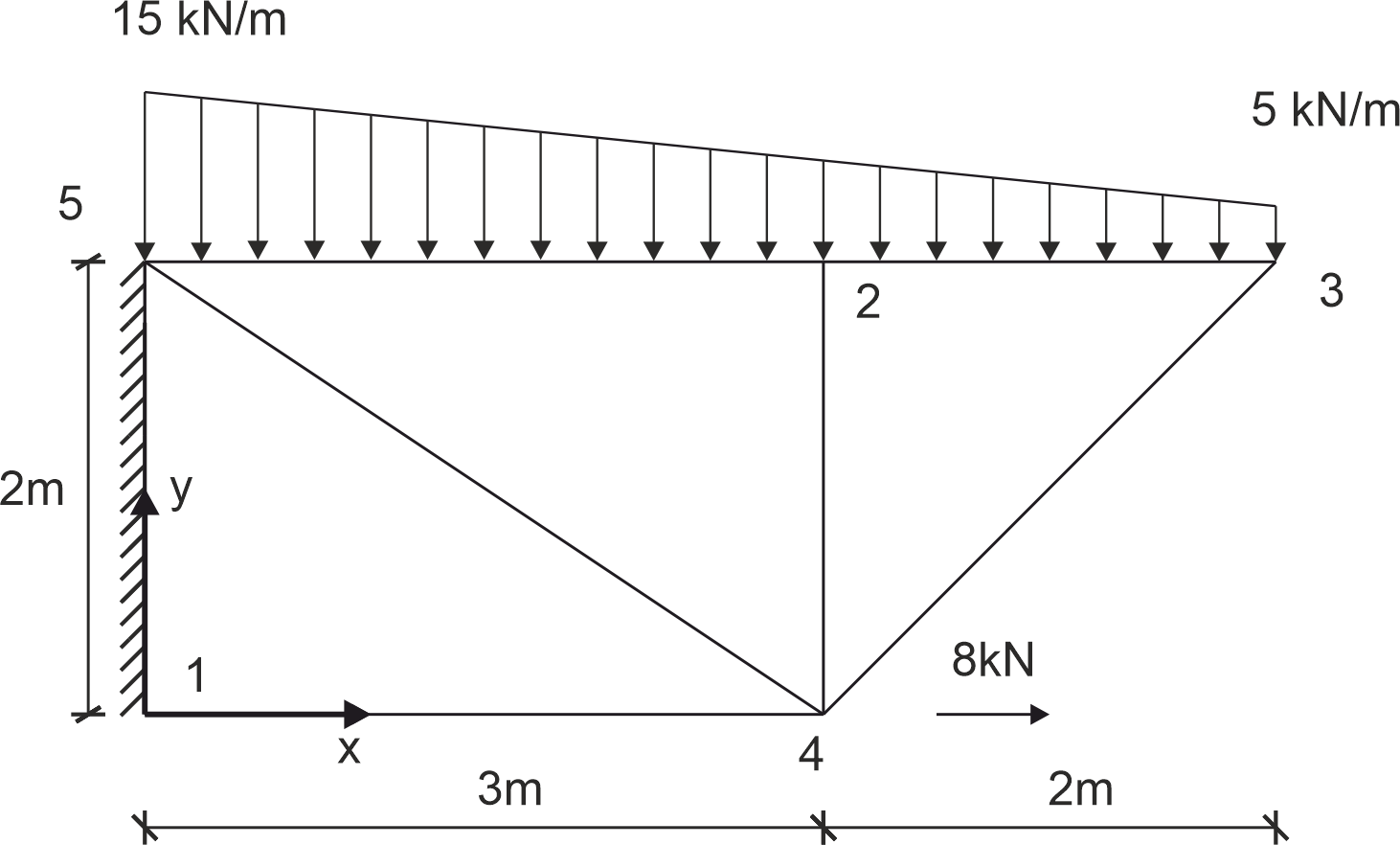
Dla podanego układu w PSO zdysektyzowanego elementami skończonymi jak na rysunku zapisać wektor obciążenia (prawej strony układu równań) MES
Przykład 3
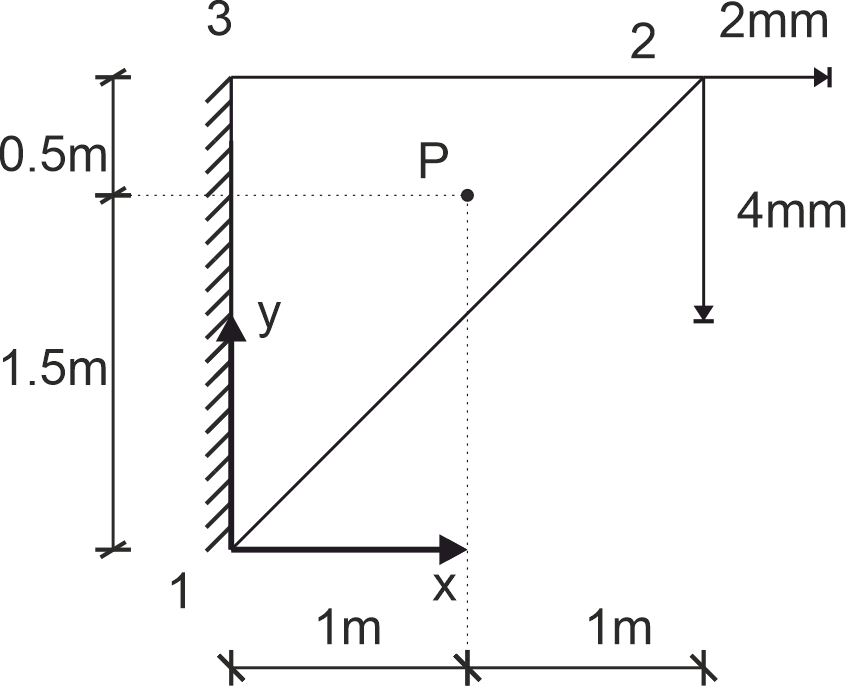
Dana jest tarcza (PSN) zdyskretyzowana 1 ES, dla której wyznaczono wartości przemieszczeń jak na rysunku. Na podstawie rozwiązania oblicz MES wektor naprężenia w punkcie P.
Przyjmij moduł Younga \( E = 20 \, \text{GPa} \), współczynnik Poissona \( \nu = 0.0 \).
Wartości naprężeń należy wyrazić w \( \text{kPa} \).
Przykład 4
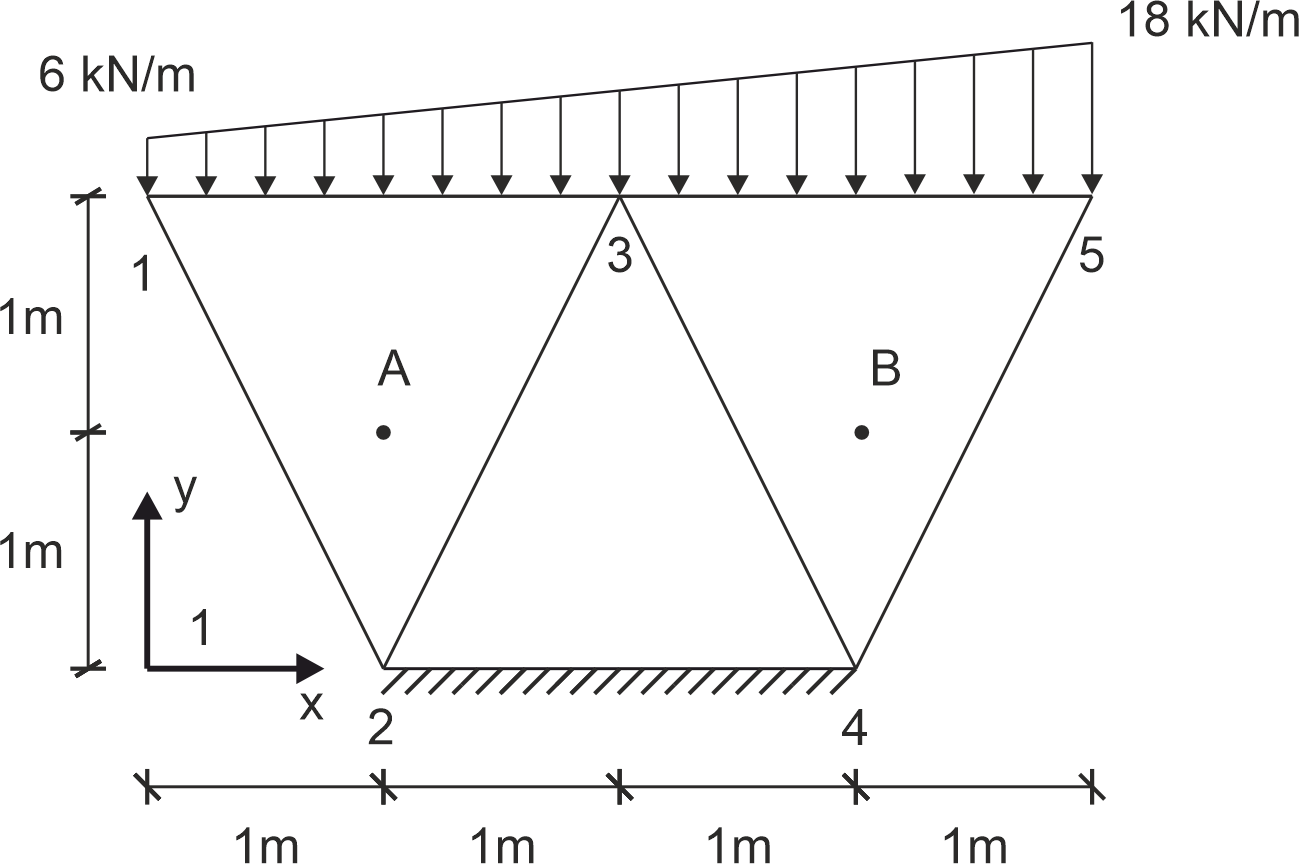
Dla podanego układu w PSO zdyskretyzowanego elementami skończonymi jak na rysunku wyznaczyć globalny wektor prawej strony równania MES oraz wyznaczyć:
1 wektor przemieszczeń \(u\)
2 wszystkie z definicji niezerowe składowe wektorów odkształcenia e i naprężenia s
w punkcie \(A\) oraz \(B\).
\[ E = 27 \, \text{GPa}, \quad \nu = 0.2 \] \[ \mathbf{d} = \begin{bmatrix} 1.90 \\ -8.86 \\ 0 \\ 0 \\ 4.74 \\ -8.73 \\ 0 \\ 0 \\ 10.4 \\ -24.5 \end{bmatrix} \cdot 10^{-7} \, \text{m} \]
Przykład 5
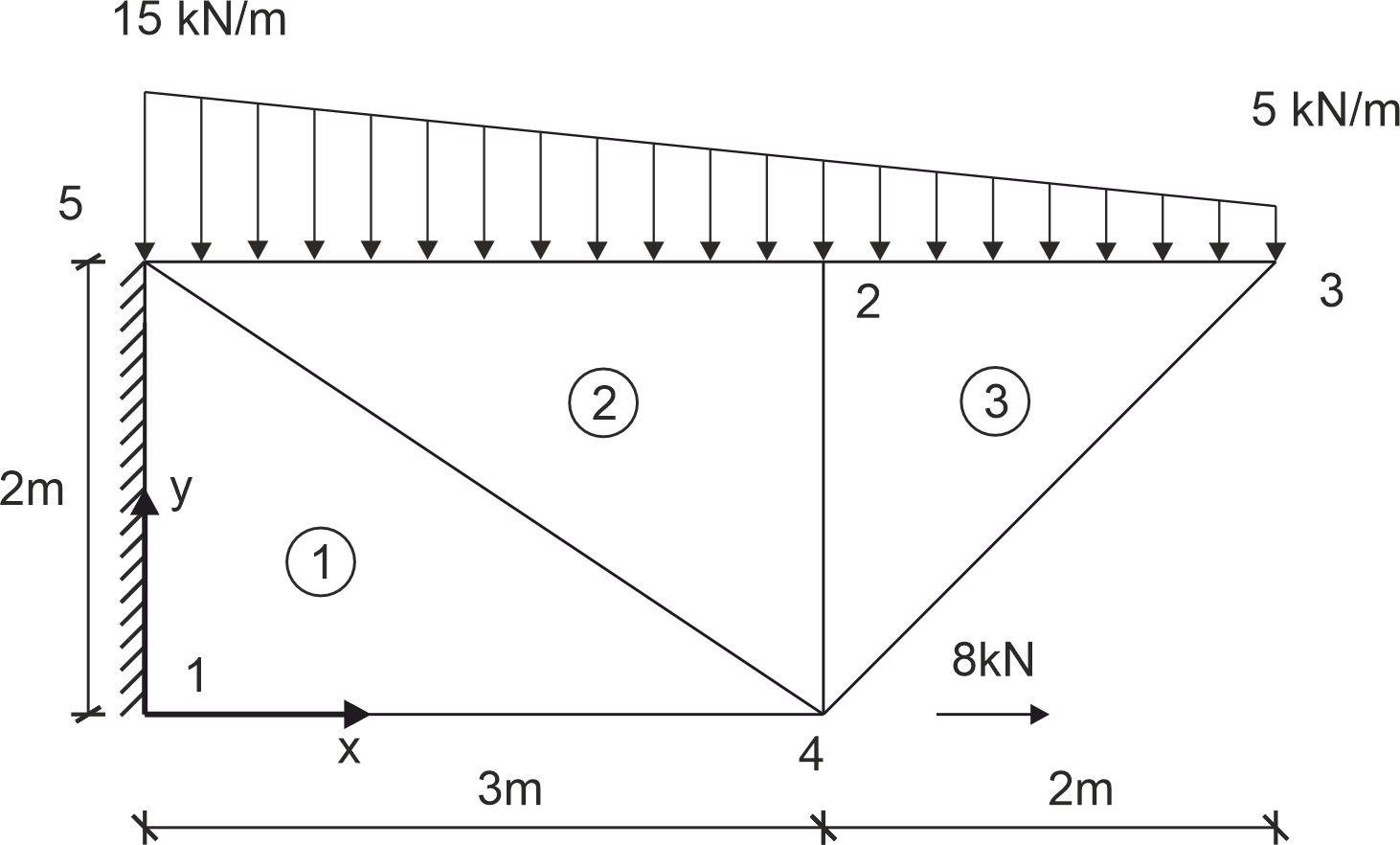
Dla podanego układu w PSO zdyskretyzowanego elementami skończonymi jak na rysunku obliczyć MES wektor odkształcenia \(e\) w środku ciężkości elementu 2. \begin{aligned} \mathbf{d} = \begin{bmatrix} 0 \\ 0 \\ 2.219 \\ -7.118 \\ 2.436 \\ -11.57 \\ -1.062 \\ -6.250 \\ 0 \\ 0 \end{bmatrix} \cdot 10^{-6} \, \text{m} \end{aligned}
Przykład 6
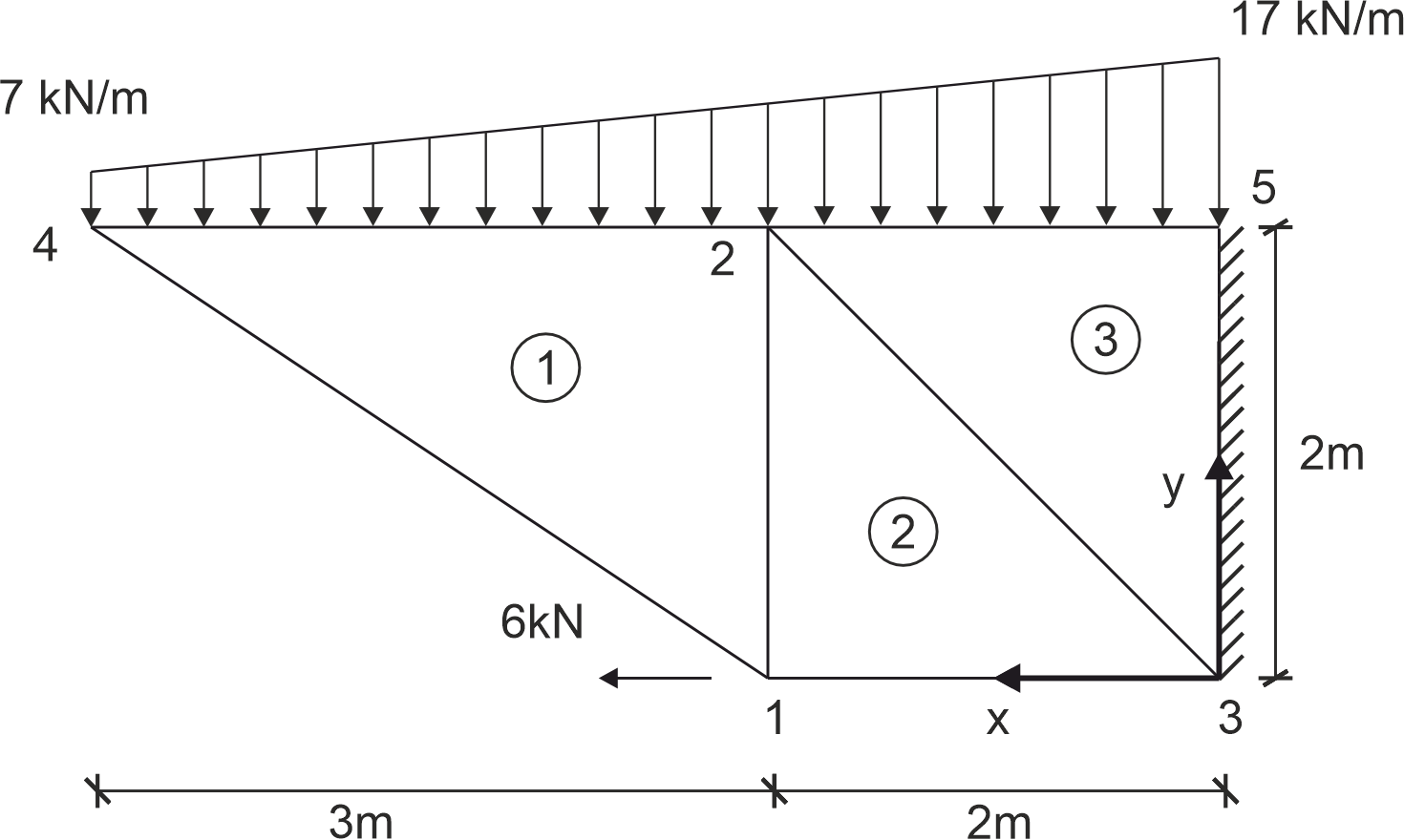
Dla podanego układu w PSO zdyskretyzowanego elementami skończonymi jak na rysunku obliczyć MES wektor odkształcenia e w środku ciężkości elementu 2. \begin{aligned} E &= 26 \, \text{GPa} \\ \nu &= 0.2 \\ d &= \begin{bmatrix} 1.727 \\ -5.973 \\ -2.178 \\ -6.116 \\ 0 \\ 0 \\ -2.231 \\ -15.71 \\ 0 \\ 0 \\ \end{bmatrix} \cdot 10^{-6} \, \text{m} \end{aligned}
Przykład 7
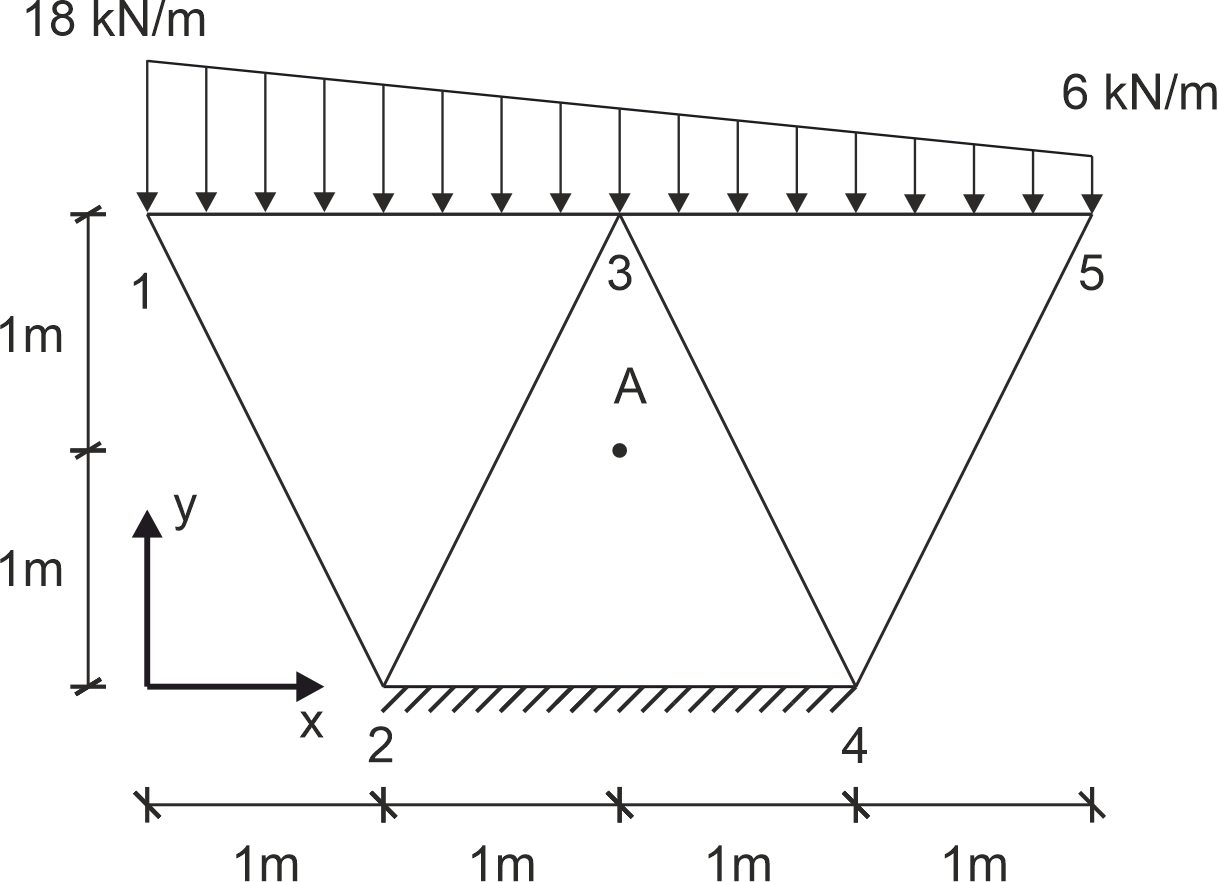
Dla podanego układu w PSO zdyskretyzowanego elementami skończonymi jak na rysunku wyznaczyć globalny wektor prawej strony równania MES oraz wyznaczyć wektor odkształcenia \( e \) w punkcie \( A \). \begin{aligned} \mathbf{d} = \begin{bmatrix} -10.4 \\ -24.5 \\ 0 \\ 0 \\ -4.74 \\ -8.73 \\ 0 \\ 0 \\ -1.90 \\ -8.86 \end{bmatrix} \cdot 10^{-7} \, \text{m} \end{aligned}
Przykład 8
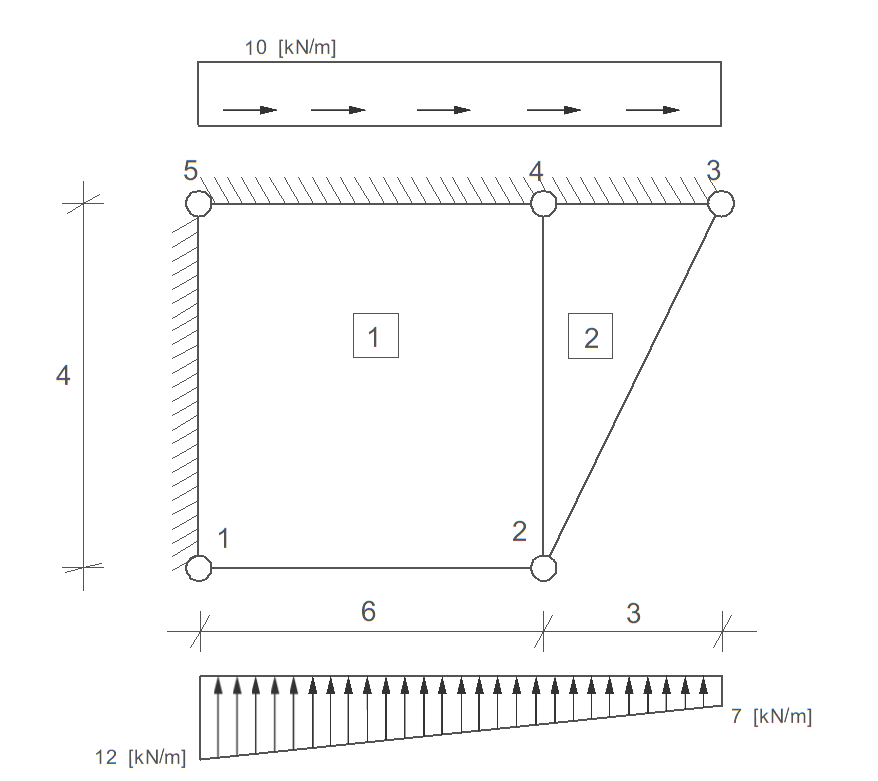
Poniższy ustrój powierzchniowy w PSO, wykonany z materiału o \( E = 40\, \text{GPa} \) i \( \nu = 0{,}25 \), rozwiązano metodą elementów skończonych. Obliczone stopnie swobody wynoszą:
\[ \mathbf{d} = [0,\ 0,\ 2,\ 4,\ 0,\ 0,\ 0,\ 0,\ 0] \cdot 10^{-5}\, \text{m} \]
Oblicz przemieszczenie w punkcie A oraz odkształcenia w elemencie 2.
Przykład 9
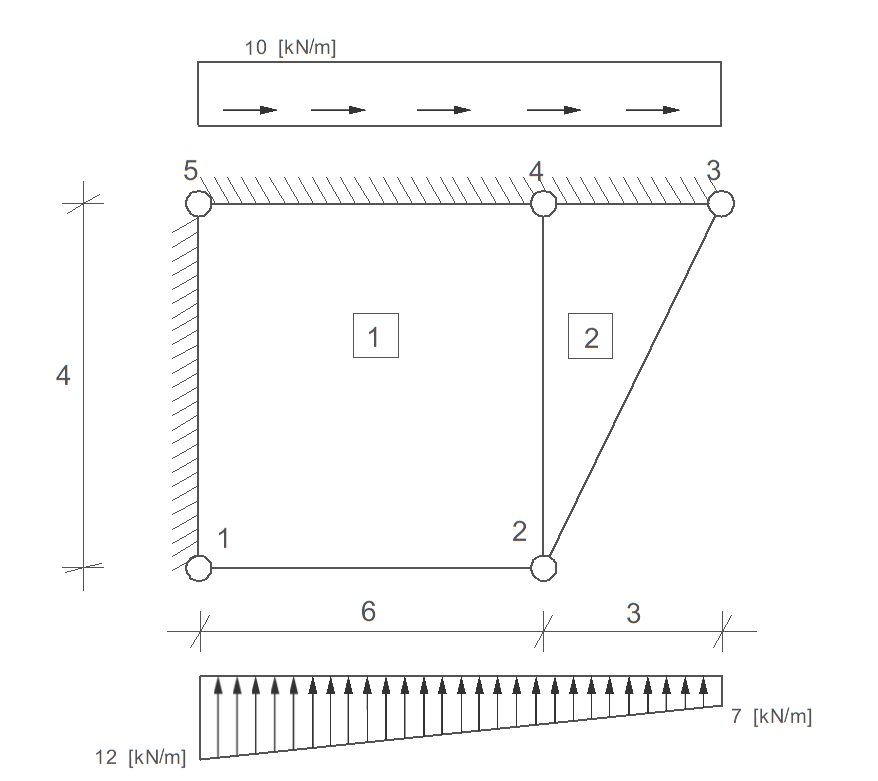
Poniższy ustrój powierzchniowy w PSO, wykonany z materiału o \( E = 20\, \text{GPa} \) i \( \nu = 0{,}20 \), rozwiązano metodą elementów skończonych. Obliczone stopnie swobody wynoszą:
\[ \mathbf{d} = [0,\ 0,\ 1,\ 2,\ 0,\ 0,\ 0,\ 0,\ 0] \cdot 10^{-5}\, \text{m} \]
Oblicz naprężenia w punkcie A
Przykład 10
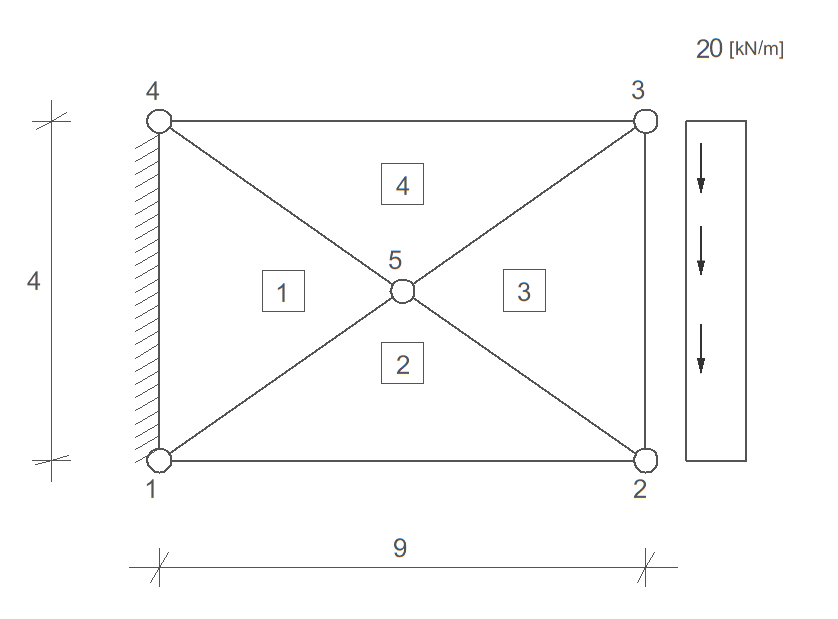
Zapisz tylko niezbędne równania MES, na podstawie których obliczysz szukane stopnie swobody (z uwzględnieniem warunków brzegowych oraz pokazując agregację). UWAGA: nie zapisuj pełnego układu równań ani nie obliczaj poszczególnych wartości elementów macierzy.