Lista zadań
Przykład 1

Dla zadanej ramy wyznaczyć częstości drgań wlasnych. $$ \begin{array}{ll} E=6 \cdot 10^7 \mathrm{~Pa} & \mu=21 \mathrm{~kg} / \mathrm{m} \\ A=1 \cdot 10^{-2} \mathrm{~m}^2 & I=9 \cdot 10^{-1} \mathrm{~m}^4 \end{array} $$
Przykład 2

Dla zadanej ramy wyznaczyć częstości drgań wlasnych. $$ \begin{array}{ll} E=6 \cdot 10^7 \mathrm{~Pa} & \mu=21 \mathrm{~kg} / \mathrm{m} \\ A=1 \cdot 10^{-2} \mathrm{~m}^2 & I=9 \cdot 10^{-4} \mathrm{~m}^4 \end{array} $$
Przykład 3

Dla zadanej ramy wyznaczyć częstotliwości drgań własnych. Naszkicować postaci drgań dla wyznaczonych częstotliwości.
\[ E = 3 \cdot 10^7 \, \text{Pa}, \quad A = 18 \cdot 10^{-3} \, \text{m}^2, \quad I = 10 \cdot 10^{-4} \, \text{m}^4, \quad \mu = 21 \, \text{kg/m} \]
Przykład 4

Dla zadanej ramy wyznaczyć częstotliwości drgań własnych. Naszkicować postaci drgań dla wyznaczonych częstotliwości.
\[ E = 3 \cdot 10^7 \, \text{Pa}, \quad A = 15 \cdot 10^{-3} \, \text{m}^2, \quad I = 5 \cdot 10^{-4} \, \text{m}^4, \quad \mu = 42 \, \text{kg/m} \]
Przykład 5
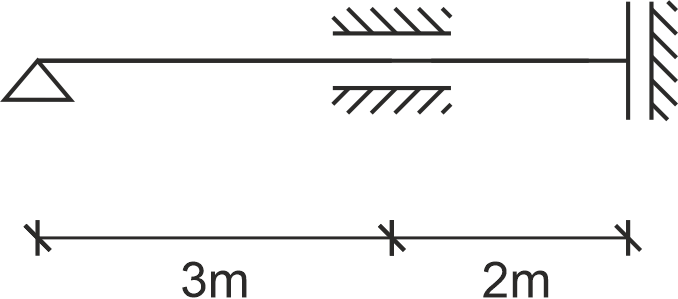
Dla zadanej ramy wyznaczyć częstości drgań własnych. \begin{aligned} E = 6 \cdot 10^7 \, \text{Pa}, \quad A = 1 \cdot 10^{-2} \, \text{m}^2, \quad I = 9 \cdot 10^{-4} \, \text{m}^4, \quad \mu = 21 \, \text{kg/m} \end{aligned}
Przykład 6
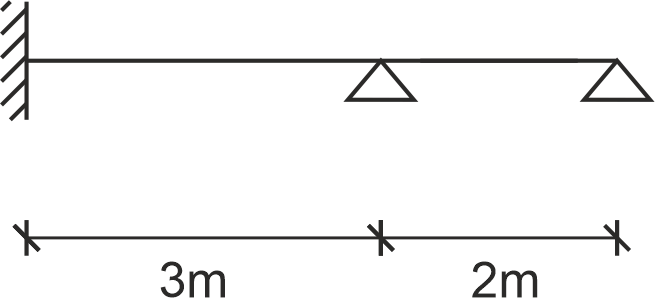
Dla zadanej ramy wyznaczyć częstotliwości drgań własnych. Naszkicować postaci drgań dla wyznaczonych częstotliwości. \begin{aligned} E = 3 \cdot 10^7 \, \text{Pa}, \quad A = 18 \cdot 10^{-3} \, \text{m}^2, \quad I = 10 \cdot 10^{-4} \, \text{m}^4, \quad \mu = 21 \, \text{kg/m} \end{aligned}
Przykład 7
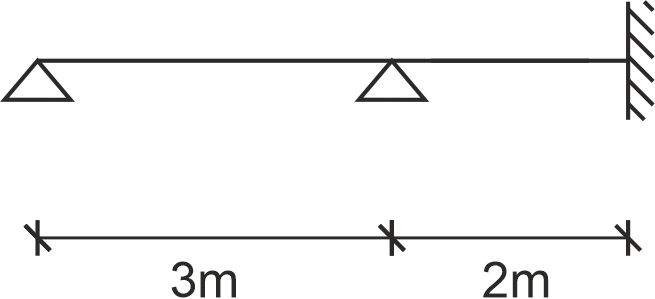
Dla zadanej ramy wyznaczyć częstotliwości drgań własnych. Naszkicować postaci drgań dla wyznaczonych częstotliwości. \begin{aligned} E = 3 \cdot 10^7 \, \text{Pa}, \quad A = 15 \cdot 10^{-3} \, \text{m}^2, \quad I = 5 \cdot 10^{-4} \, \text{m}^4, \quad \mu = 42 \, \text{kg/m} \end{aligned}
Przykład 8
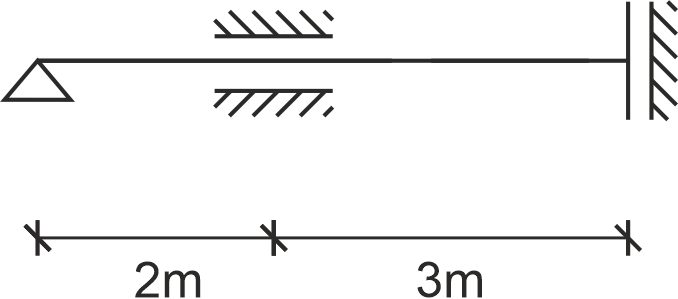
Dla zadanej ramy wyznaczyć częstotliwości drgań własnych. \begin{aligned} E = 6 \cdot 10^7 \, \text{Pa}, \quad A = 1 \cdot 10^{-2} \, \text{m}^2, \quad I = 4 \cdot 10^{-4} \, \text{m}^4, \quad \mu = 42 \, \text{kg/m} \end{aligned}
Przykład 9
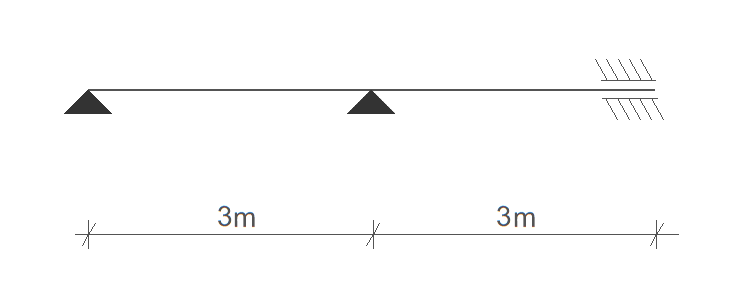
Dla zadanej ramy utworzyć układ równań MES z uwzględnieniem warunków brzegowych dla problemu własnego zapisanego w celu wyznaczenia częstotliwości drgań własnych.
\[ E = 3 \cdot 10^7 \, \text{Pa} \qquad \mu = 21 \, \text{kg/m} \qquad A = 1 \cdot 10^{-2} \, \text{m}^2 \qquad I = 9 \cdot 10^{-4} \, \text{m}^4 \]
Przykład 10
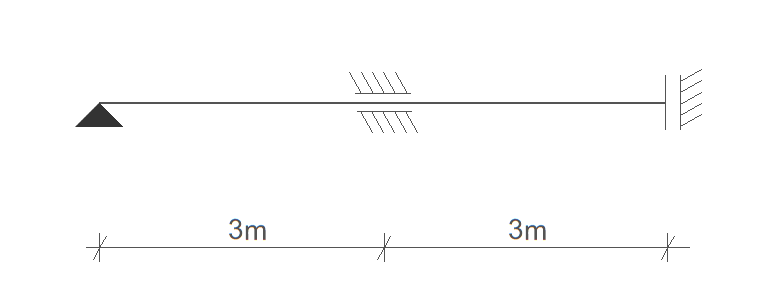
Dla zadanej ramy utworzyć układ równań MES z uwzględnieniem warunków brzegowych dla problemu własnego zapisanego w celu wyznaczenia częstotliwości drgań własnych.
\[ E = 3 \cdot 10^7 \, \text{Pa} \qquad \mu = 42 \, \text{kg/m} \qquad A = 1 \cdot 10^{-2} \, \text{m}^2 \qquad I = 9 \cdot 10^{-4} \, \text{m}^4 \]
Przykład 11
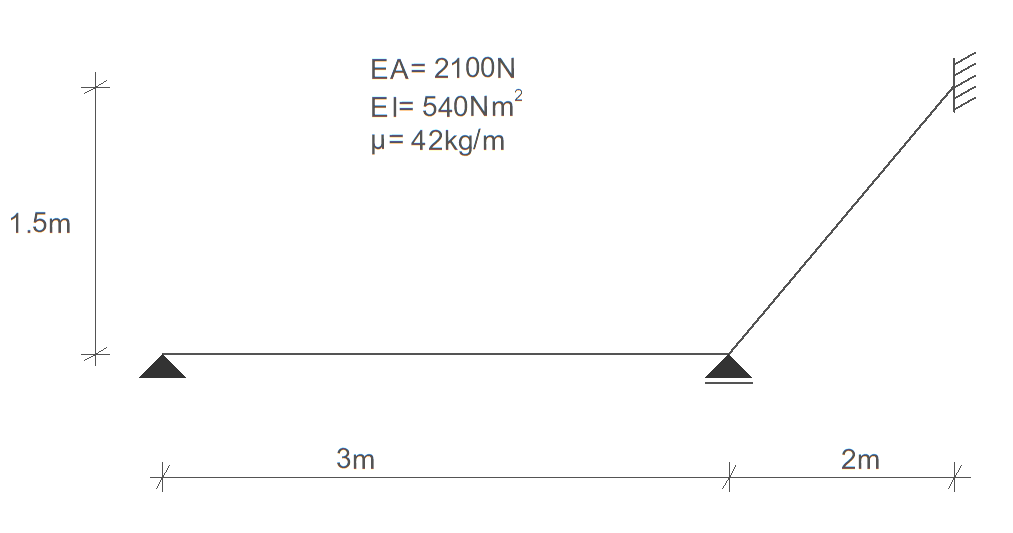
Dla zadanej ramy utworzyć układ równań MES z uwzględnieniem warunków brzegowych dla problemu własnego zapisanego w celu wyznaczenia częstotliwości drgań własnych.
Przykład 12

Dla zadanej ramy utworzyć układ równań MES z uwzględnieniem warunków brzegowych dla problemu własnego zapisanego w celu wyznaczenia drgań własnych
\[ EA= 2100 \, \text{N}, \quad EI = 540 \, \text{Nm}^2 \quad \mu = 42 \, \text{kg/m} \]