Lista zadań
Przykład 1
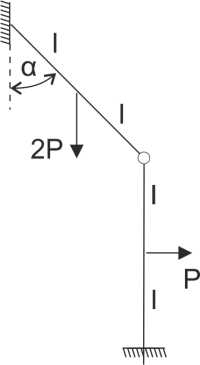
Pręt skośny podparty jest o ścianę i połączony przegubowo z prętem pionowym, który jest utwierdzony. Uwolnij układ od więzów i zapisz równania równowagi statycznej.
Przykład 2
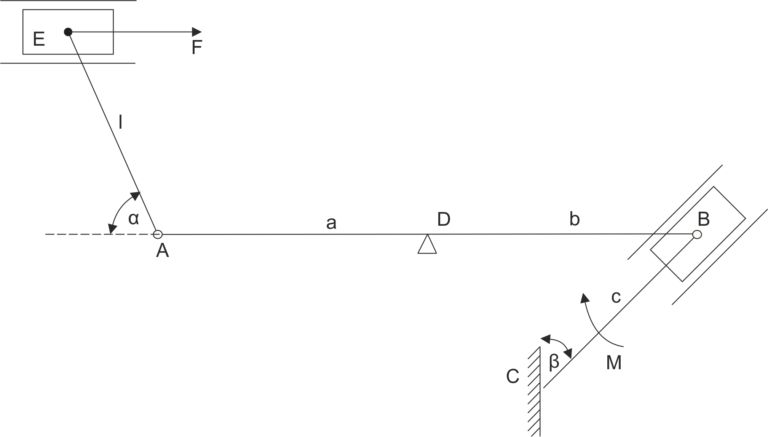
Dany jest układ trzech prętów połączonych przegubowo. Dolny pręt jest podparty swobodnie o ostoję. Uwolnij układ od więzów, zapisz równania równowagi statycznej.
Przykład 3
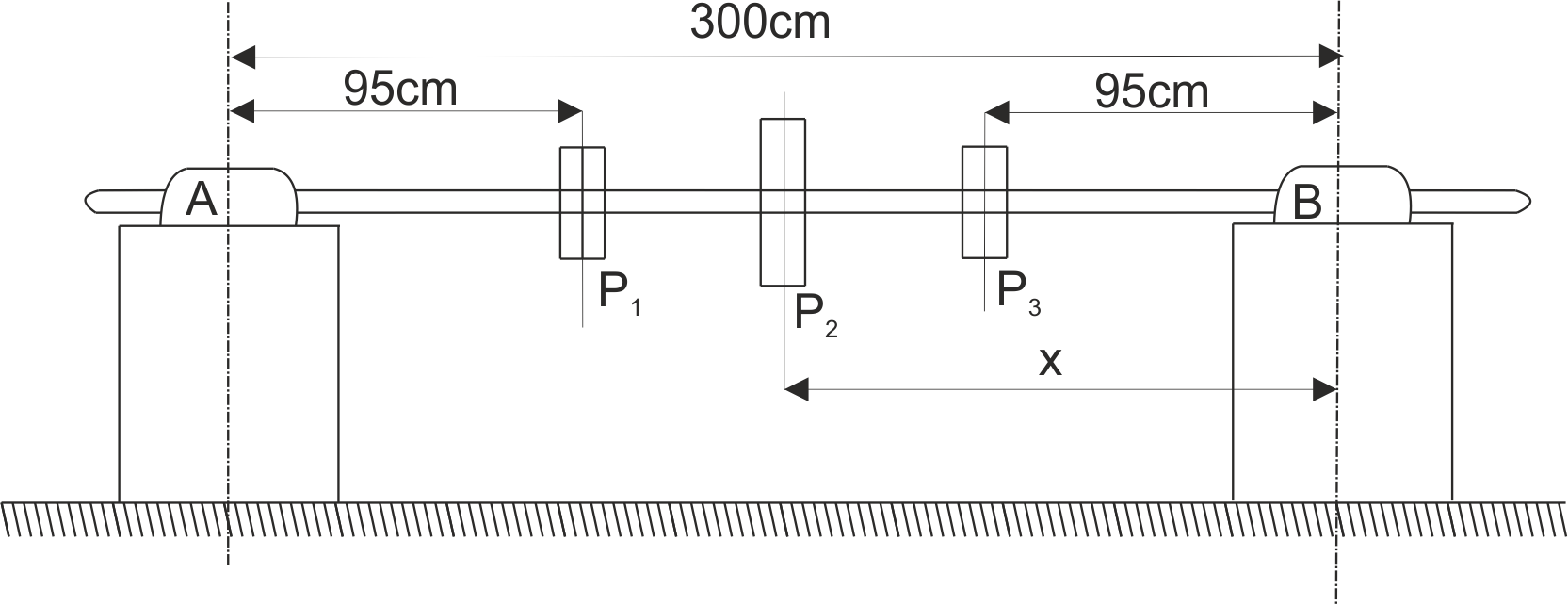
Wał transmisyjny AB ma trzy koła pasowe o ciężarach P1=3 kN, P2=5 kN, P3=2 kN. Wymiary pokazano na rysunku. W jakiej odległości x od łożyska B należy zamocować koło o ciężarze P2, aby reakcje obydwu łożysk były sobie równe? Pomijamy ciężar wału.
Przykład 4
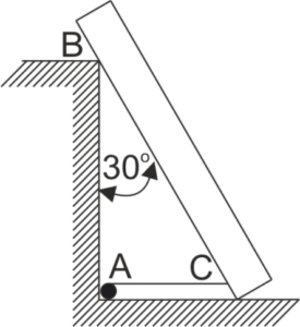
Jednorodna belka o masie 60 kg i długości 4 m, opierająca się jednym końcem na gładkiej podłodze, a w pośrednim punkcie B – na słupie o wysokości 3 m, tworzy z pionem kąt \(30^o\). Belka utrzymywana jest w takim położeniu przez sznur AC przeciągnięty wzdłuż podłogi. Wyznaczyć siłę T w sznurze oraz reakcje w punktach B i C.
Przykład 5
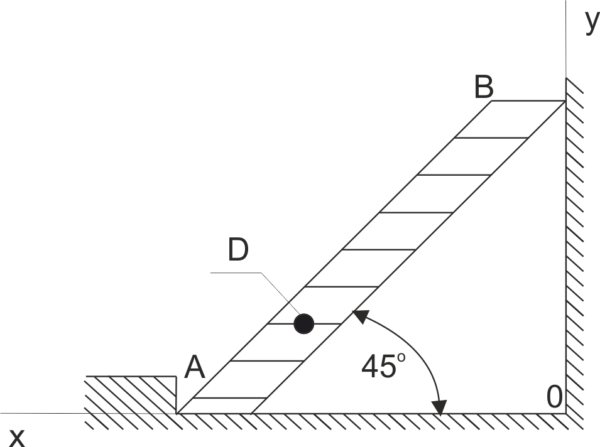
Do gładkiej ściany jest przystawiona drabina AB, nachylona pod kątem 45^o do poziomu. Masa drabiny wynosi 20 kg. W punkcie D odległym od dolnego końca o 1/3 długości drabiny stoi człowiek o masie 60 kg. Wyznaczyć siły nacisku drabiny na podporę A i na ścianę.
Przykład 6
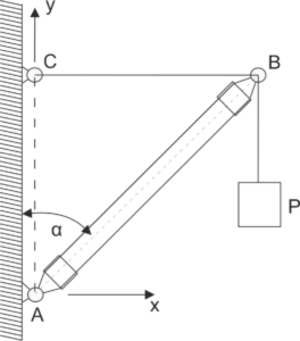
Dźwig składa się z belki AB, której dolny koniec połączony jest przegubem A ze ścianą, a górny podtrzymywany poziomą liną BC. Wyznaczyć napięcie T liny BC i rzut pionowy \(N_A\) nacisku na podporę A, jeżeli ciężar P wynosi P=2 kN, ciężar belki Q=1 kN jest zaczepiony w połowie długości AB, a kąt \( \alpha=45^o \).
Przykład 7
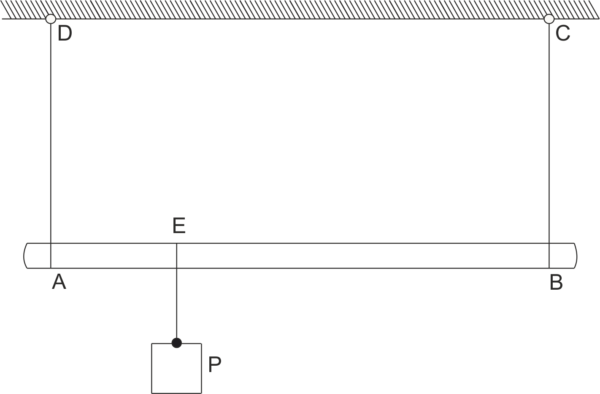
Jednorodny pręt AB o długości 1 m i ciężarze 20 N zawieszony jest poziomo na dwóch równoległych linkach AC i BD. Na pręcie w punkcie E, odległym od punktu A o 0,25 m zawieszono ciężar P=120 N. Obliczyć siły w linkach \( T_{AC}, T_{BD} \).
Przykład 8
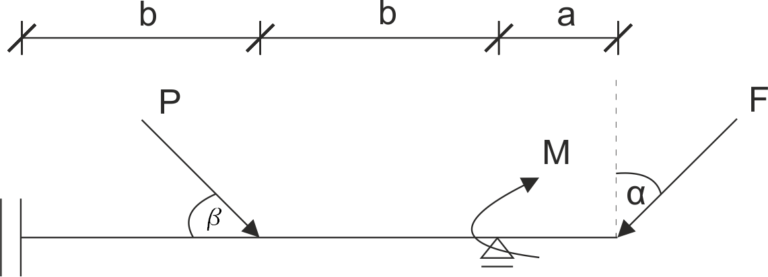
Dana jest belka podparta łyżwą pionową i podporą przegubowo przesuwną. Uwolnij układ od więzów i zapisz równania równowagi statycznej.
Przykład 9
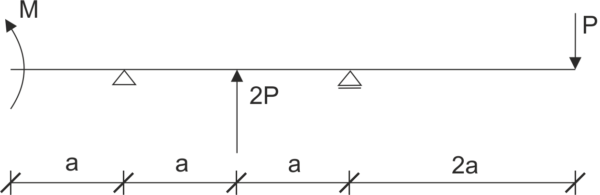
Dana jest belka podparta jak na rysunku. Uwolnij układ od więzów i zapisz równania równowagi.
Przykład 10
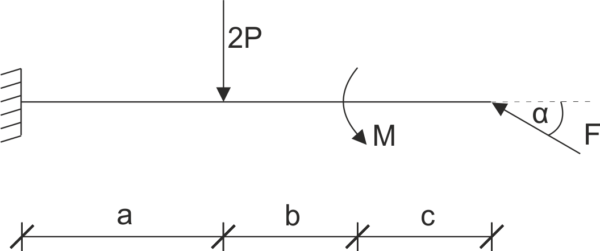
Dana jest belka podparta jak na rysunku. Uwolnij układ od więzów i zapisz równania równowagi.
Przykład 11
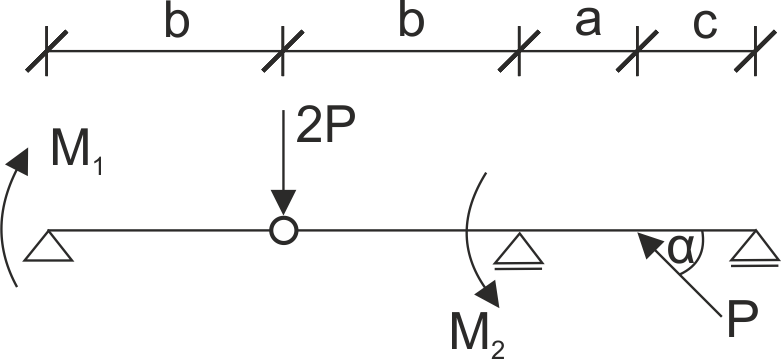
Dana jest belka podparta jak na rysunku. Uwolnij układ od więzów, podziel belkę przegubową na belki proste i zapisz równania równowagi.
Przykład 12
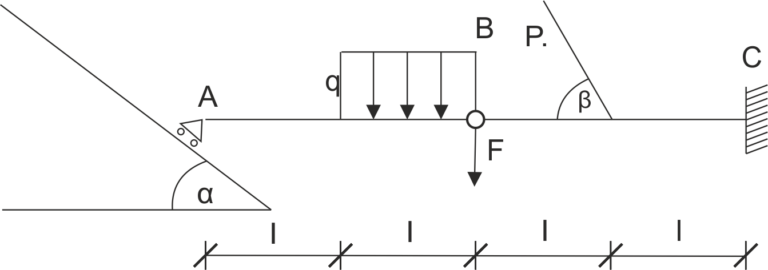
Dana jest belka podparta jak na rysunku. Uwolnij układ od więzów, podziel belkę przegubową na belki proste i zapisz równania równowagi.