Lista zadań
Przykład 1
Rurociag o średnicy D=200mm podłączono do zbiornika z wodą. Nad powierzchnią wody w zbiorniku panuje nadciśnienie \( p_{n1} = 800 hPa \) które wskazuje manometr. Na rurociągu w odległości L=102m zamontowano manometr, który wskazuje nadciśnienie \( p_{n2} = 700 hPa \). Obliczyć natężenie przeływu wody w rurociąga mając dane: \( H=1m, \: kolano \: r/D = 4, k=1\cdot 10^{-5}m \nu = 1,306\cdot 10^{-6}, \rho = 1000 \frac{kg}{m^3} \).
Przykład 2

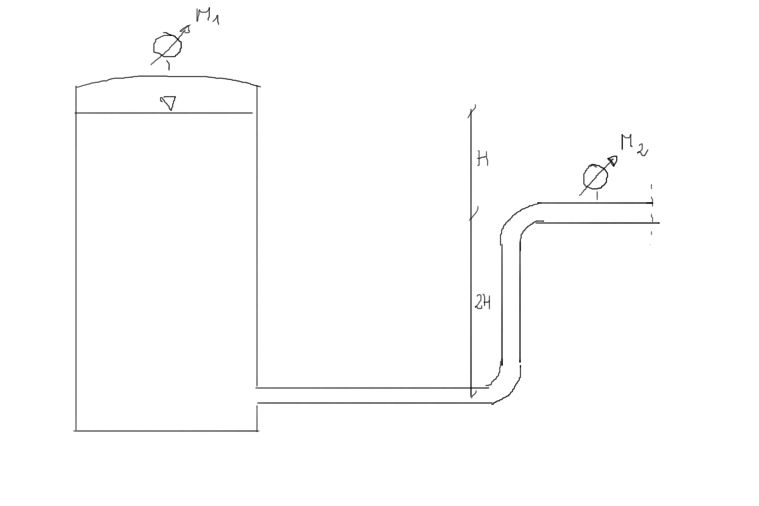
1. Obliczyć H - poziom zwierciadła w zbiorniku, aby prędkość na wypływie wyniosła \( v= 2\frac{m}{s} \)
2. Naszkicować piezometryczną linię ciśnień i linie energii.
Dane:
\(
L_1 = 100m,
L_2 =200m,
D_1 = 200mm,
D_2 =100mm,
\rho=1000 \frac{kg}{m^3},
\nu = 1,306*10^{-6} \frac{m^2}{s},
k=0,2mm
\)
Straty - na wylocie ze zbiornika: \(\xi_{1} =0,5\)
Straty - na zwężeniu \(\xi_{2} =0,38\)
Straty - na zaworze \(\xi_{2} =5,3\)
Przykład 3

Woda znajdująca się w górnym zamkniętym zbiorniku pod ciśnieniem \( p_n = 10000 N/m^2 \) przepływa do dolnego, otwartego zbiornika. Określić strumień objętości wody.
Dane:
\begin{aligned}
& H_1 = 10m \\
& H_2 = 1m \\
& H_3 = 2m \\
& d = 100mm \\
& D = 200mm \\
& \xi_1 = 0,5 \\
& \xi_2 = 0,29 \\
& \xi_3 = 0,56 \\
& \xi_4 = 0,37 \\
& \xi_5 = 4 \\
& \xi_6 = 1 \\
& \lambda = 0,03 \\
& L_D = 1m \\
& L_d = 14m \\
\end{aligned}
Przykład 4
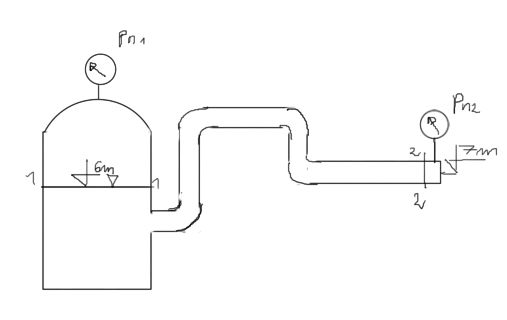
Sprawdź kierunek przepływu i dobierz średnicę rurociągu, w którym płynąć ma woda o wydatku Q. Nadciśnienie powietrza w zbiorniku wynosi \(p_{n1}\). Nadciśnienie mierzone manometrem zainstalowanym na rurociągu w odległości L od zbiornika powinno wynosić \(p_n{2}\). Przyjmij że średnica wewnątrz przewodów w typoszeregu zmienia się co 5mm. Współczynnik strate miejscowych na każdym z kolan wynosi \( \xi_{kol} \), zaś na wlocie \( \xi_{wl} \). Chropowatość bezwzględna przewodu wynosi k, zaś kinematyczny współczynnik lepkości wynosi \( \nu \).
Dane:
\begin{aligned}
&Q = 15 l/s\\
&p_{n1} = 1bar\\
&p_{n2} = 80kPa\\
&L=100m\\
&k=0,1mm\\
&\xi_{kol}=0,18\\
&\xi_{wl}=0,2\\
&\nu=1,306 \cdot 10^{-6} m^2/s
\end{aligned}