Lista zadań
Przykład 1

Dla układu złożonego z części stożkowej i kulistej jak na rysunku:
- Proszę podać czas wypływu cieczy z części stożkowej zbiornika
- Po opróżnieniu części stożkowej, proszę podać czas opróżniania części kulistej zbiornika
- Proszę podać całkowitą objętość cieczy w zbiorniku w litrach
- Proszę podać powierzchnię zwierciadła cieczy na poziomie z=2R
- Proszę podać całkowity czas wypływu cieczy w minutach
Dane:
Przykład 2
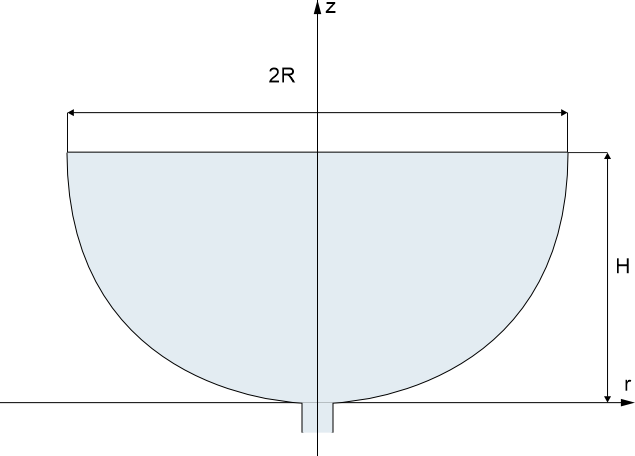
Otwarte naczynie w kształcie paraboloidy obrotowej o promieniu \(\mathrm{R}=1 \mathrm{~m}\) i wysokości \(\mathrm{H}=1 \mathrm{~m}\) napełniono całkowicie wodą. Z naczynia woda wypływa do atmosfery przez mały otwór o średnicy \(\mathrm{d}=5 \mathrm{~mm}\) i współczynniku wydatku \(\mu=0,8\). Obliczyć czas, po którym w naczyniu pozostanie \(1 / 4\) pierwotnej objętości wody.
Przykład 3
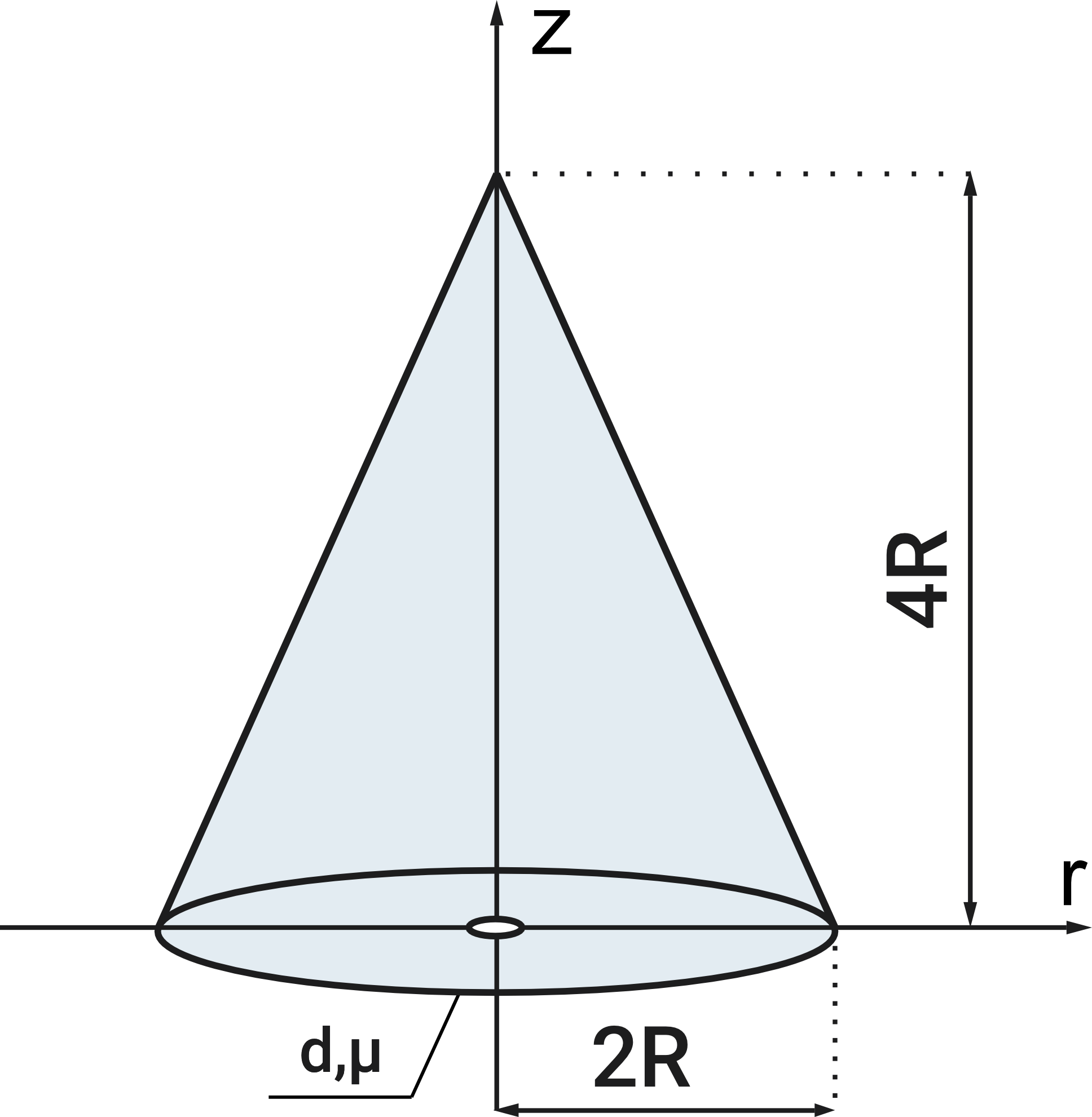
Zbiornik w kształcie prostego stożka kołowego o promieniu podstawy równym \(\mathbf{2 R}\) i wysokości \(\mathbf{4 R}\) napełniono całkowicie wodą. Obliczyć czas, po którym ze zbiornika wypłynie \(1 / 4\) jego pierwotnej objętości, jeżeli \(\mathbf{R}=\mathbf{0 , 5} \mathrm{m}\), średnica otworu przez który woda wypływa ze zbiornika wynosi \(\mathbf{d}=\mathbf{5}[\mathrm{mm}]\), natomiast współczynnik wydatku wynosi \(\boldsymbol{\mu}=\mathbf{0 , 8}\).
Przykład 4
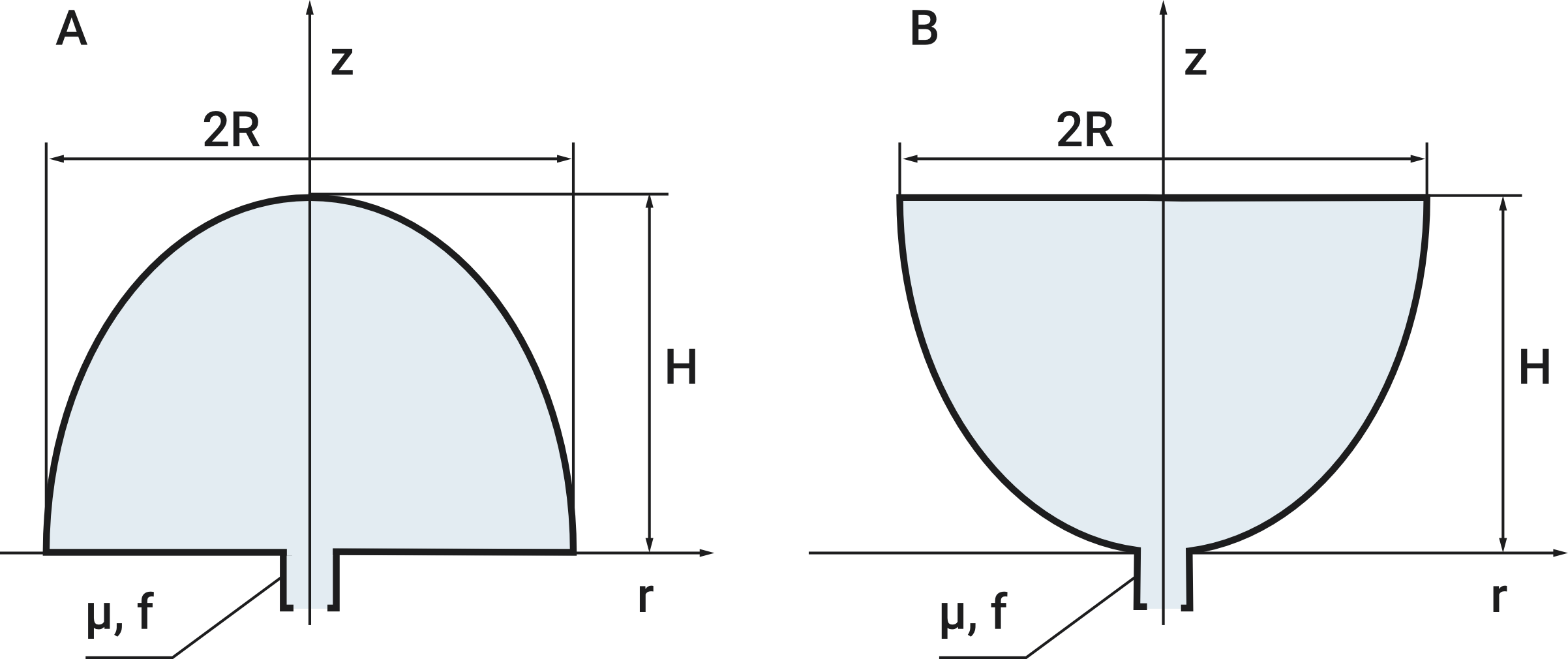
Zbiorniki A B w kształcie paraboloidy obrotowej napełniono całkowicie cieczą o ciężarze właściwym \(\gamma\). Obliczyć stosunek czasów \(t_A\) i \(t_B\) wypływu cieczy ze zbiorników A i B \(\frac{t_A}{t_B}=\) ?