Rozwiązanie
Zobacz więcej na temat całkowania metodą Wereszczagina.
Rozwiązanie zadania:
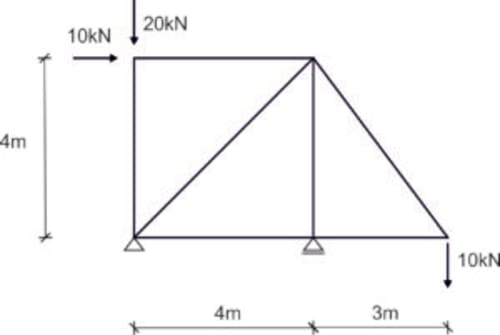
Numerujemy pręty i zaznaczamy reakcje podporowe w celu obliczenia ich wartości. Kąt alfa jest między prętem 2 i 3.
Dążymy do obliczenia wartości sił normalnych we wszystkich prętach kratownicy od obciążenia zewnętrznego.
 \begin{array}{lll}
\sum{X}=0 & H_A=-10\ kN \\
\sum{M_A}=0 & 10\cdot4+10\cdot7-4V_B=0 &\ V_B=27,5\ kN \\ \sum{M_B}=0 & V_A\cdot4+10\cdot4-20\cdot4+10\cdot3=0 &\ V_A=2,5\ kN \\ \sum{Y}=0 & V_A+V_B-20-10=0 &\ L=P \\
\end{array}
\begin{array}{lll}
\sum{X}=0 & H_A=-10\ kN \\
\sum{M_A}=0 & 10\cdot4+10\cdot7-4V_B=0 &\ V_B=27,5\ kN \\ \sum{M_B}=0 & V_A\cdot4+10\cdot4-20\cdot4+10\cdot3=0 &\ V_A=2,5\ kN \\ \sum{Y}=0 & V_A+V_B-20-10=0 &\ L=P \\
\end{array}
Liczymy siły we wszystkich prętach korzystając z dowolnej metody, w tym przykładzie skorzystaliśmy z metody równoważenia węzłów.
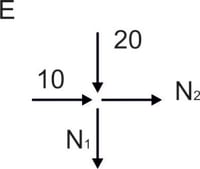 \begin{aligned}
&\sum{X}=0 & N_2+10=0 \\ &\sum{Y}=0 &-20- N_1=0 \\ &N_1=-20\ kN \\ &N_2=-10\ kN \\
\end{aligned}
\begin{aligned}
&\sum{X}=0 & N_2+10=0 \\ &\sum{Y}=0 &-20- N_1=0 \\ &N_1=-20\ kN \\ &N_2=-10\ kN \\
\end{aligned}
 \begin{aligned}
&\sum{Y}=0 & N_1+2,5+N_3\cdot\frac{\sqrt{2}}{2}=0 \\ &\sum{X}=0 &-10+N_4 +N_3\cdot\frac{\sqrt{2}}{2}=0 \\ &N_3=\frac{35\sqrt{2}}{2}\ kN \\ &N_4=7,5\ kN \\
\end{aligned}
\begin{aligned}
&\sum{Y}=0 & N_1+2,5+N_3\cdot\frac{\sqrt{2}}{2}=0 \\ &\sum{X}=0 &-10+N_4 +N_3\cdot\frac{\sqrt{2}}{2}=0 \\ &N_3=\frac{35\sqrt{2}}{2}\ kN \\ &N_4=7,5\ kN \\
\end{aligned}
 \begin{array}{lll}
&\sum{X}=0 & N_6=N_4=7,5\ kN \\ &\sum{Y}=0 &N_5=-27,5 \ kN\\
\end{array}
\begin{array}{lll}
&\sum{X}=0 & N_6=N_4=7,5\ kN \\ &\sum{Y}=0 &N_5=-27,5 \ kN\\
\end{array}
 \begin{aligned}
&\sum{Y}=0 & N_7\cdot0,8-10=0 \\ &\sum{X}=0 &-N_6-N_7\cdot0,6=0 \\ &N_7=12,5\ kN \\ &L=P \\
\end{aligned}
\begin{aligned}
&\sum{Y}=0 & N_7\cdot0,8-10=0 \\ &\sum{X}=0 &-N_6-N_7\cdot0,6=0 \\ &N_7=12,5\ kN \\ &L=P \\
\end{aligned}
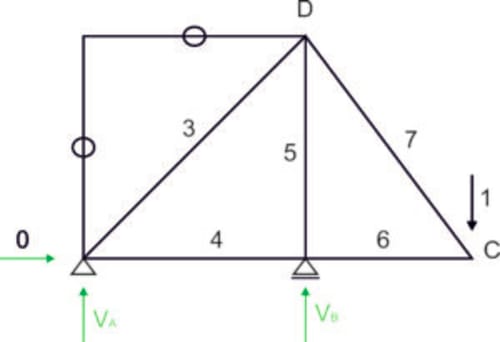
W celu obliczenia przemieszczenia przykładamy siłę uogólnioną odpowiadającą temu przemieszczeniu. Ponownie liczymy reakcje podporowe i siły we wszystkich prętach od wirtualnego obciążenia.
 \begin{aligned}
\sum{M_A}=0 & -4V_B+7=0 &\ V_B=\frac{7}{4}\ kN \\ \sum{M_B}=0 & V_A\cdot4+3=0 &\ V_A=-\frac{3}{4}\ kN \\
\end{aligned}
\begin{aligned}
\sum{M_A}=0 & -4V_B+7=0 &\ V_B=\frac{7}{4}\ kN \\ \sum{M_B}=0 & V_A\cdot4+3=0 &\ V_A=-\frac{3}{4}\ kN \\
\end{aligned}
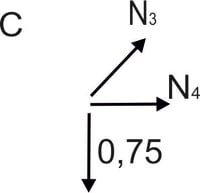 \begin{aligned}
&\sum{Y}=0 & -\frac{3}{4}+N_3\cdot\frac{\sqrt{2}}{2}=0 \\ &\sum{X}=0 &N_4 +N_3\cdot\frac{\sqrt{2}}{2}=0 \\ &N_3=\frac{3\sqrt{2}}{4}\ kN \\ &N_4=-\frac{3}{4}\ kN \\
\end{aligned}
\begin{aligned}
&\sum{Y}=0 & -\frac{3}{4}+N_3\cdot\frac{\sqrt{2}}{2}=0 \\ &\sum{X}=0 &N_4 +N_3\cdot\frac{\sqrt{2}}{2}=0 \\ &N_3=\frac{3\sqrt{2}}{4}\ kN \\ &N_4=-\frac{3}{4}\ kN \\
\end{aligned}
 \begin{array}{lll}
&\sum{X}=0 &N_6=N_4=-\frac{3}{4}\ kN \\ &\sum{Y}=0 &N_5=-\frac{7}{4} \ kN\\
\end{array}
\begin{array}{lll}
&\sum{X}=0 &N_6=N_4=-\frac{3}{4}\ kN \\ &\sum{Y}=0 &N_5=-\frac{7}{4} \ kN\\
\end{array}
 \begin{array}{ll}
\sum{Y}=0 &N_7\cdot0,8-1=0 \\ &N_7=\frac{5}{4} \ kN
\end{array}
\begin{array}{ll}
\sum{Y}=0 &N_7\cdot0,8-1=0 \\ &N_7=\frac{5}{4} \ kN
\end{array}
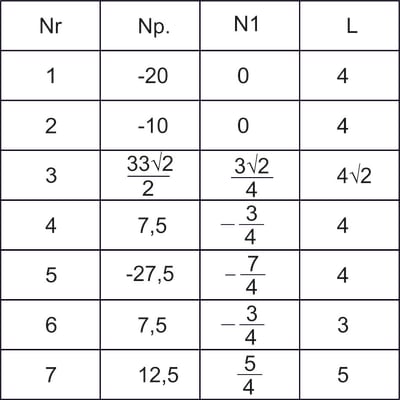
W celu uproszczenia obliczeń wygodnie jest zrobić sobie tabelkę, szczególnie w arkuszu kalkulacyjnym. Szukane przemieszczenie jest to przecałkowany wykres sił normalnych od obciążenia zewnętrznego i wirtualnego, a ponieważ te wykresy są prostokątne to sprowadza się to do przemnożenia w każdym wierszu siły w stanie P, jednostkowym i długości pręta (całkowanie dwóch prostokątów ze sobą), a następnie zsumowaniu wyników. Uzyskana suma podzielona przez sztywność na rozciąganie EA to szukane przemieszczenie.
 \begin{aligned}
&E=205GPa\\
&A=30 cm^2\\
&EA=615\cdot10^6\\
\end{aligned}
\begin{aligned}
\Delta Y_{C}=\sum\frac{N_P\cdot N_1\cdot l_i}{EA}=\frac{379,7424\cdot10^3}{615\cdot10^6}=0,6174mm\\
\end{aligned}
\begin{aligned}
&E=205GPa\\
&A=30 cm^2\\
&EA=615\cdot10^6\\
\end{aligned}
\begin{aligned}
\Delta Y_{C}=\sum\frac{N_P\cdot N_1\cdot l_i}{EA}=\frac{379,7424\cdot10^3}{615\cdot10^6}=0,6174mm\\
\end{aligned}
