Lista zadań
Przykład 1
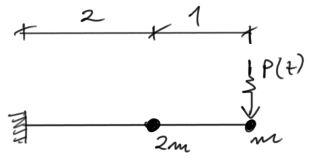
Dla podanej belki wyznaczyć częstości drgań własnych i narysować ich postacie. Sprawdzić warunek ortogonalności. Narysować momenty ostateczne pochodzące od sił bezwładności (częstość wymuszenia przyjąć jako średnią arytmetyczną wyliczonych wcześniej częstości drgań własnych, czyli \( \theta=\frac{\omega_1+\omega_2}{2} \) ) \( \text{Dane:} \ EI= 2,1\cdot 10^5 \ kNm^2, \ m=200 \ kg, \ P=10\cdot sin(\theta \ t) \)
Przykład 2

Dla podanej ramy wyznaczyć siły bezwładności. \( \text{Dane:} \ EI= 4000 \ kNm^2, \ m=700 \ kg, \ P=25 sin(pt), \ p=15\ \frac{rad}{s} \)
Przykład 3
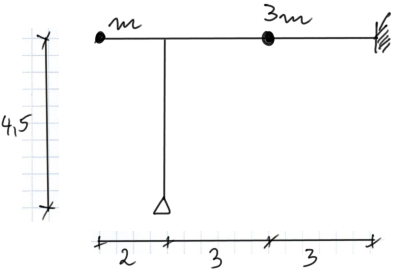
Dla podanej ramy narysować momenty ostateczne pochodzące od sił bezwładności. Narysować obwiednie momentów. Dane: \( \mathrm{E}=2.1 \cdot 10^{11} \frac{\mathrm{N}}{\mathrm{m}^2}, \mathrm{~m}=660 \mathrm{~kg}, \mathrm{~m}_{\mathrm{w}}=2250 \mathrm{~kg}, \mathrm{e}=4.3 \mathrm{~mm}, \mathrm{n}=470 \frac{\mathrm{obr}}{\mathrm{min}} \), przekrój belki IPN 200.
Przykład 4
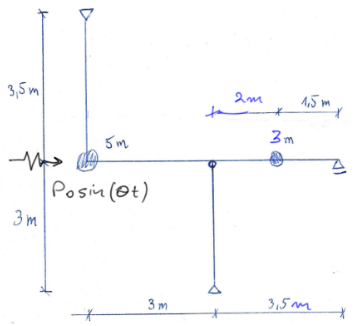
Dla podanej ramy narysować momenty ostateczne pochodzące od sił bezwładności. Narysować obwiednie momentów. Dane: \( \mathrm{E}=2.1 \cdot 10^{11} \frac{\mathrm{N}}{\mathrm{m}^2}, \mathrm{~m}=680 \mathrm{~kg}, \mathrm{~m}_{\mathrm{w}}=400 \mathrm{~kg}, \mathrm{e}=2 \mathrm{~mm}, \mathrm{n}=300 \frac{\mathrm{obr}}{\mathrm{min}} \), przekrój ramy o momencie bezwładności \(I=4250\ cm^4 \).
Przykład 5
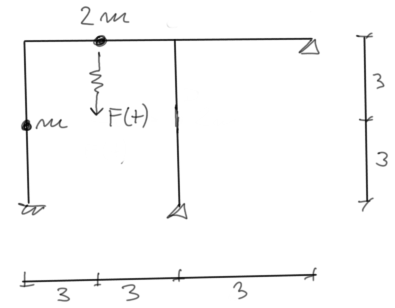
Dla podanej ramy narysować momenty ostateczne pochodzące od sił bezwładności. Dane: \( \theta =0,8\cdot \omega_1 \, F_0=2\ kN \)
Przykład 6
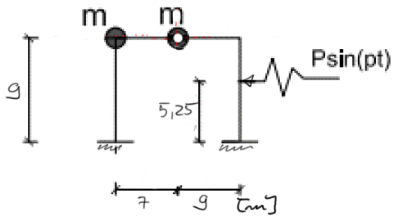
Dla podanej ramy narysować momenty ostateczne pochodzace od sł bezwładności. Sprawdzić czy naprężenia w pręcie o przekroju prostokątnym 12 x 24 cm oraz module Younga 210 GPa nie przekroczą dopuszczalnej wytrzymałości kg=240 MPa. Dane: \( \mathrm{p}=8.25 \frac{\mathrm{rad}}{\mathrm{s}}, \mathrm{m}=2.75 \mathrm{t}, \mathrm{P}=20.5 \mathrm{kN} \)