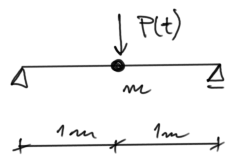
Rozwiązanie
Stopień statycznej niewyznaczalności
SSN=3-3=0Liczba stopni swobody dynamicznej
LSSD=1
\( m_1=m \)
W miejscu i na kierunku swobody dynamicznej przykładamy siłę jednostkową i rysujemy wykres momentów od takiego obciążenia
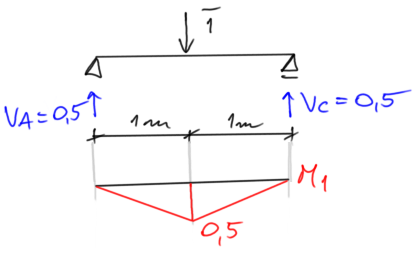
Delta dynamiczna $$ \delta_{11}:=\frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} \cdot 0.5 \cdot 0.5 \cdot 1+\frac{1}{3} \cdot 0.5 \cdot 0.5 \cdot 1\right)=\frac{1}{6} \cdot \frac{1}{\mathrm{EI}} $$ Problem własny dynamiki dla LSSD=1 $$ \left(\delta_{11} \cdot \mathrm{m}_1 \cdot \omega^2-1\right) \cdot \mathrm{A}=0 $$ Dzieląc obustronie przez A i przekształcając równanie otrzymujemy \begin{aligned} &\omega_1 =\sqrt{\frac{1}{m_1 \cdot \delta_{11}}}\\ &\text{Sztywność na zginanie} \\ &EI=210\cdot 10^9 \cdot 10\cdot 10^{-8}=21 000 Nm^2 \\ &\text{Częstość drgań własnych: }\\ &\omega_1 =\sqrt{\frac{1}{10\cdot \frac{1}{6\cdot 21 000}}}=112,25\frac{rad}{s}\\ \\ \end{aligned}
Zamiana częstości wymuszającej na jednostkę podstawową (z Hz na rad/s), uwaga - częstość wymuszająca bywa podawana również symbolem θ lub p.
\begin{aligned} &\text{Częstość wymuszająca: }\\ &\omega_w = 2\pi \cdot f_v=2\cdot \pi \cdot 5=31,42\frac{rad}{s}\\ \end{aligned}Rezonans zachodzi jeżeli częstość wymuszająca jest zbyt blisko częstości drgań własnych, przyjmuje się, że częstość wymuszająca nie może się zawierać w przedziale pomiędzy 0,85ω a 1,15ω.
\( \omega_w/\omega_1=31,42/112,25=0,28 \)Nie zachodzi rezonans.
Amplituda drgań wymuszonych
\( \left(\delta_{11} \cdot m_1 \cdot \omega_w^2-1\right) \cdot A+\Delta_{1 p}=0 \)
Jeżeli siła wymuszająca jest na stopniu swobody dynamicznej, wówczas
\( \Delta_1p=\delta_{11}\cdot P \) \begin{aligned} &A=\frac{\delta_{11}\cdot P}{1-\omega_w^2 \cdot \delta_{11} \cdot m}\\ &A=\frac{\frac{1}{6\cdot 21 000}\cdot 100}{1-31,42^2 \cdot \frac{1}{6\cdot 21 000} \cdot 10}=8,61\cdot 10^{-4}m=0,86 mm\\ \\ &\text{Siła bezwładności:}\\ &B=\frac{\delta_{11} \cdot P}{\frac{1}{\omega_w^2 \cdot m}-\delta_{11}}\\ &B=\frac{\frac{1}{6\cdot 21 000} \cdot 100}{\frac{1}{31,42^2 \cdot 10}-\frac{1}{6\cdot 21 000}}=8,5 N\\ \end{aligned}