Edupanda » Strength of materials » Zero force members
Zero Force Members
In this text you will learn what are zero force members and find examples of trusses with determination of zero force members
↓ link to exercises with solutions and video courses ↓
Truss - a structure composed of straight members connected at joints by pin connections and subjected to concentrated forces at the joints. Pin connections imply that the internal forces in truss members are purely axial (longitudinal, normal) forces.


↓ link to exercises with solutions and video courses ↓
Watch video course for this topic!
(identify zero force members and
determine forces in members using Ritter's method)
Watch video course for this topic!
(identify zero force members and
determine forces in members using method of nodes equilibrium)
Browse exercises for this topic!
(determine forces in members using method of nodes equilibrium)
Browse exercises for this topic!
(determine forces in members using Ritter's method)
Truss - a structure composed of straight members connected at joints by pin connections and subjected to concentrated forces at the joints. Pin connections imply that the internal forces in truss members are purely axial (longitudinal, normal) forces.
Zero Force Members

Theorem I
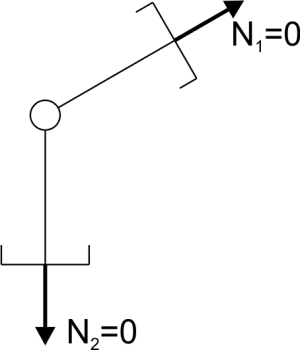
If two members in a truss meet at a joint and the joint is unloaded, the internal forces in both members are equal to zero.
Theorem II
If two members in a truss meet at a joint and the joint is loaded by a force acting in the direction of one of the members, the internal force in the other member is equal to zero.
Theorem III
If three members meet at a joint in a truss, with two members lying on the same straight line and the joint is unloaded, the internal force in the third member is equal to zero.Example 1
See theoretical introduction for Ritter's method
See theoretical introduction for Method of nodes equilibrium

Example 2
Text
For the truss shown in the diagram, determine the number of zero force members.
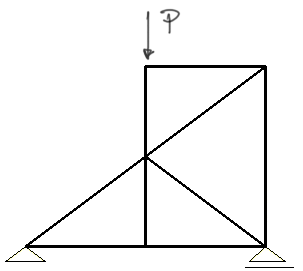
Solution
Step 1
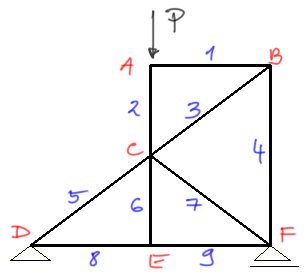
Number the members and label the joints.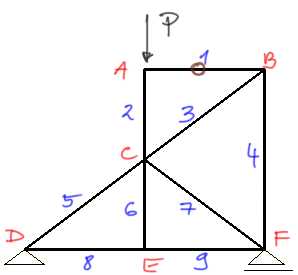
Step 2
From the second theorem, member number 1 is a zero force member, so mark this member as "0" in brown.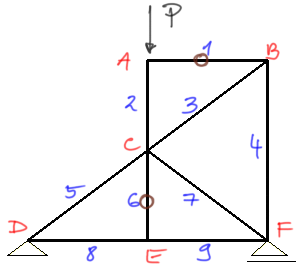
Step 3
At the same time, from the third theorem, member number 6 is a zero force member - mark it.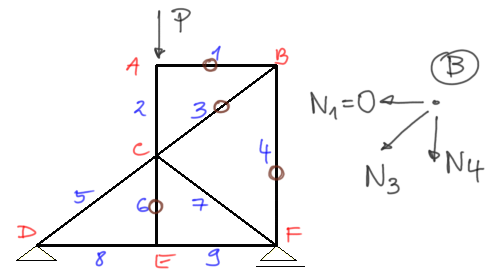
Step 4
Now the most interesting step, we need to look at joint B, if we previously identified member number 1 as a zero force member, we can now say that only two members (instead of three) converge at joint B (because one member in this case is a zero force member). Therefore, according to the first theorem - if two members converge at a joint and it is unloaded, both members are zero force members - members number 3 and 4 will be zero force members.Example 3
Text
For the truss shown in the diagram, determine the number of zero force members.

Solution
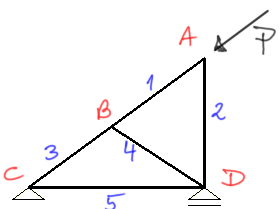
Step 1
Numbering the rods, marking the nodes.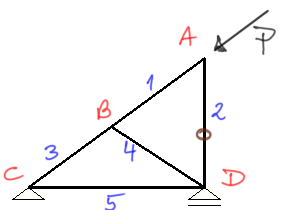
Step 2
I notice from the 2nd law that rod no. 2 is zero, and I mark this rod in brown as "0".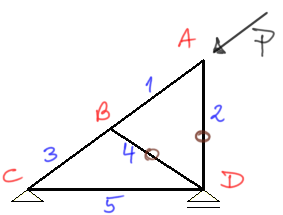
Step 3
At the same time, I notice that from the 3rd law rod number 4 is zero (I look at node B).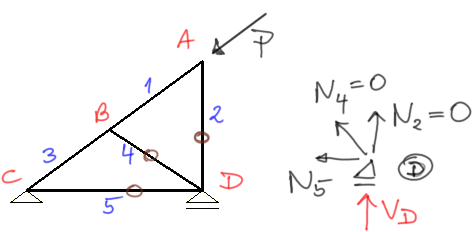
Step 4
Due to the fact that rods 2 and 4 are zeroes, if we look at node D, we will see that it is acted upon by the force in rod 5 and the reaction VD. From the 2nd law, we determine that rod no. 5 is zero.Example 4
Content
For the truss as shown in the drawing, determine the number of zero rods.
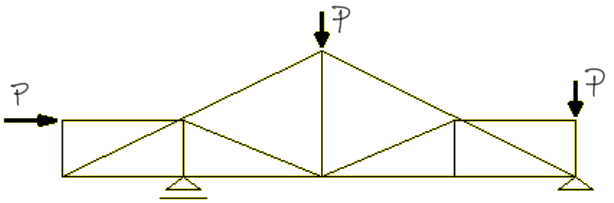
Solution
Step 1
Numbering the rods, marking the nodes.

Step 2
I notice from the 2nd law that rods: no. 5 and no. 6 are zero. I also notice that rod no. 11 is zero (from the 3rd law) and mark these rods in brown as "0".
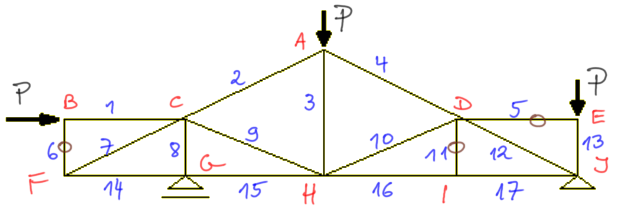
Step 3
I mentally remove the zero rods from the truss and notice that in node F there are two rods and it is unloaded - therefore rod no. 7 and rod no. 14 are zero (1st law). In node D there are three rods left, two of which are collinear and the node is unloaded, so according to the 3rd law rod no. 10 is zero.
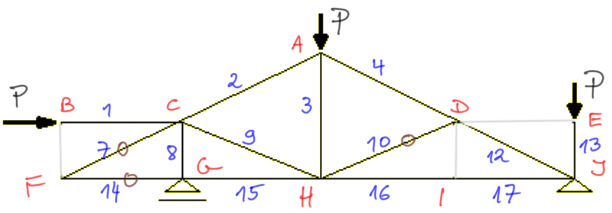
Step 4
I removed more zero rods mentally and now I notice that the 2nd law applies in node G. There are two rods in the node, and the reaction VG acts vertically, i.e. collinearly with rod 8, so rod no. 15 will be zero.
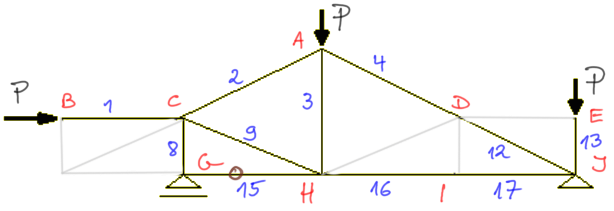
In this way, we have identified 7 rods as zero.
↓ link to the task database with solutions and video courses ↓
See the offer and price of tutoring

|
Łukasz CichowiczTel: +48 780 155 029E-mail: lukasz@edupanda.pl Skype: edupandapl |