Problem

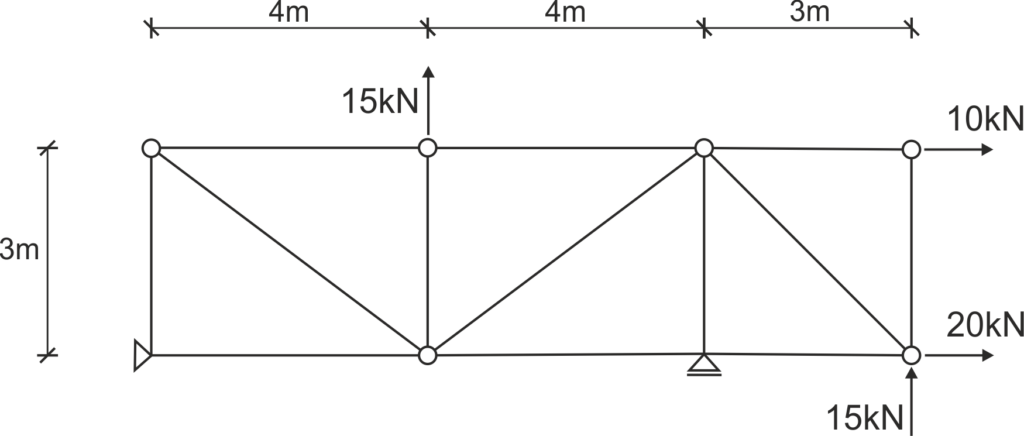
Solution

Step 1

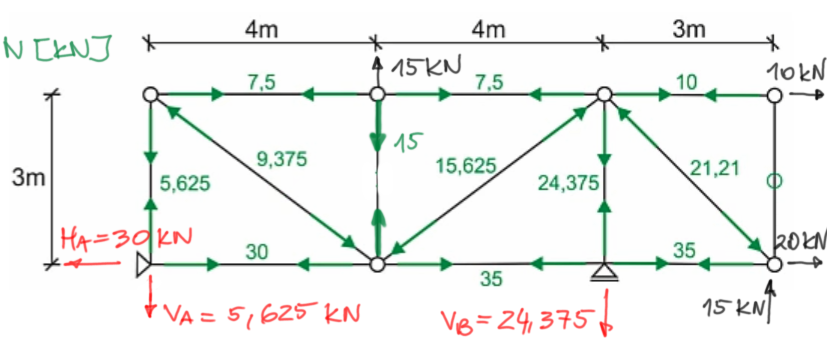
Numbering the members, possibly marking nodes, indicating support reactions.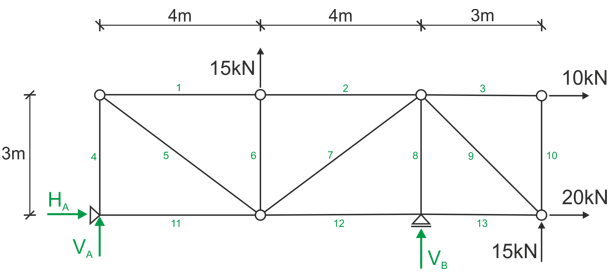

Step 2

Writing out static equilibrium equations and calculating support reactions.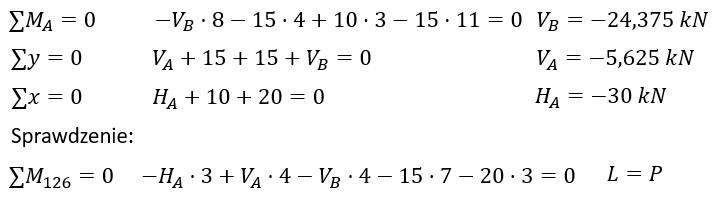

Step 3

We make sections.

We can basically start in any way, as long as we don't cut through more than 3 members, because that's how many unknowns we can calculate in one section.
Let's start by cutting through members 2, 7, and 12 and make a view from the left side

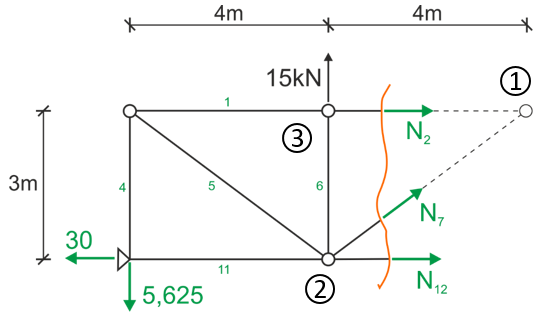
We write static equilibrium equations.

The so-called Ritter points are the intersection points of the directions of two unknowns.
In the figure above, forces N2 and N7 intersect at point (1) and forces N7 and N12 intersect at point (2) - these are the Ritter points. Most often we write sums of moments at Ritter points, it happens that there are more than two such points if the forces are at different angles, then we can write three equations in the form of sum of moments.
If, however, we have only two Ritter points as here, it doesn't matter, we write two sums of moments and as the third equation we can write either the sum of projections on the "x" axis. or (better) on "y", because only the unknown N7 enters this equation.
We can also write the sum of moments at another point, so as to calculate the last unknown, here point (3) was determined.

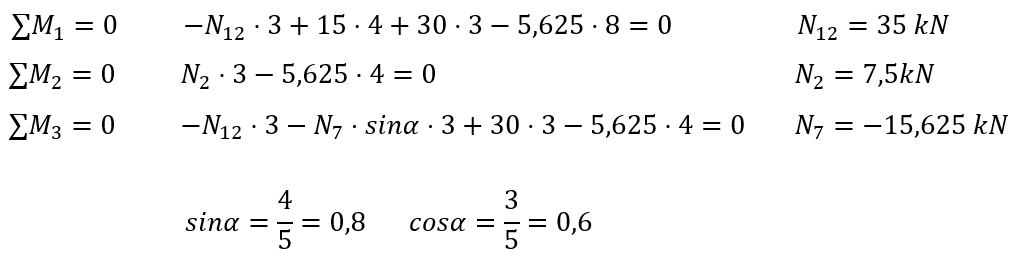
Similarly, we do in a section through members 1,5,11.

View from the left side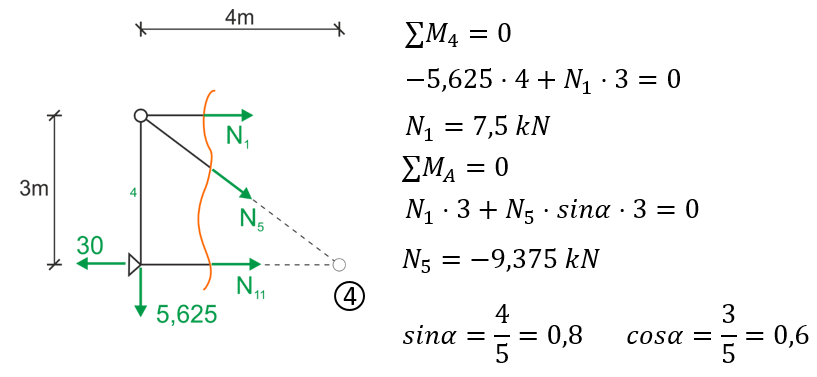

The last will be a section through members 3,9,13.

View from the right side

Step 5

Completing the solution of the problem.
Let's draw a diagram of normal forces in the members we have already calculated.
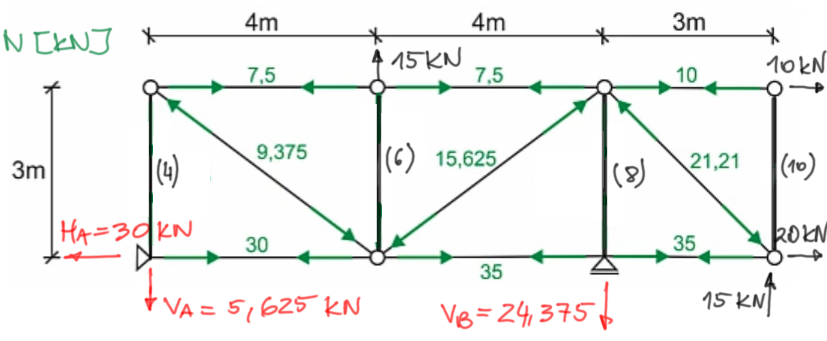
Normal force diagram, sign convention:
POSITIVE

NEGATIVE

We have calculated forces in most of the members (9 out of 13). We are left with 4 members (vertical 4,6,8 and 10), we have three options:

- make more sections, but we need four separate cuts to calculate these forces, which somewhat defeats the purpose.
- do the equilibrium of joints A,B, (3-10) and (1-2-6) and calculate the last four forces, certainly less drawing by cutting out a single joint than making a larger section,
- cleverly notice that:

1) from the second theorem on zero force members, member (10) is zero,

2) from the second theorem, in principle, it follows
an additional rule - if a force loads a joint in such a way that its direction is collinear with one of the members and no other force can be projected onto this line, then the force in the member is transmitted collinearly.
Let's look at the bottom chord and joint B - the 35kN force in the horizontal member passes from member to member as seen in the diagram
while the reaction VB=24.375 kN loads member (8) collinearly - so it directly transmits a tensile force to it (because we see that reaction VB acts on member (8) in such a way that it stretches it).
ultimately from this we know the force in member (8)

3) on the same principle N6=15 kN

4) on the same principle N4=5.625 kN

Step 6

We draw the final normal force diagram.