Edupanda » Strength of Materials » Mohr's Method
Mohr's Method - displacement calculation
In this text you will learn about what Mohr's Method is and what is the algorithm for solving problems involving displacements using this method.
In the first step, we deal with the standard distribution of shear forces in a specific (given) beam. Then, in the second step, we focus on determining the distribution of moments in the so-called "equivalent beam".
For the equivalent beam (secondary, fictitious beam), we choose the geometry, support, and loading in such a way that, based on the solution of the first step, we obtain a distribution of moments that is numerically identical to the deflection distribution in the real beam.
To better understand, please see the example below


They will be equal to the corresponding displacements at the same point in the axis of the real beam.
-> The shear force at point K in the equivalent beam corresponds to the rotation angle at point K in the real beam,
-> The bending moment at point K in the equivalent beam corresponds to the deflection of the real beam at that point.
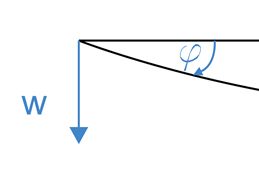
In the adopted reference system, displacement w>0 is directed downward, and a positive rotation angle \(\varphi>0\) is consistent with clockwise rotation.
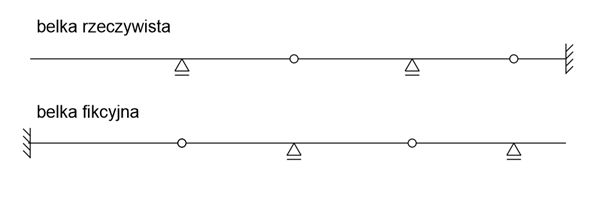
Transformation of the real beam into the fictitious beam
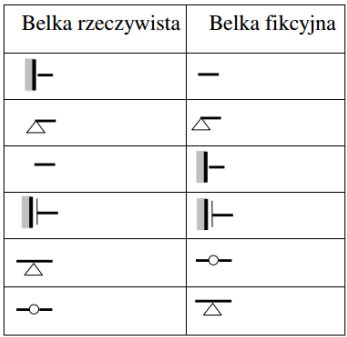
\(\kappa=\frac{\alpha \Delta T}{h}\)
Then, the load on the fictitious beam has the value of κ and is directed towards the warmer fibers.
Mohr's Method
Mohr's Method, also known as grapho-analytical method, equivalent beam method, secondary loading method, or graphical method, is based on a two-step approach for solving the problem of determining the distribution of bending moments in a beam.In the first step, we deal with the standard distribution of shear forces in a specific (given) beam. Then, in the second step, we focus on determining the distribution of moments in the so-called "equivalent beam".
For the equivalent beam (secondary, fictitious beam), we choose the geometry, support, and loading in such a way that, based on the solution of the first step, we obtain a distribution of moments that is numerically identical to the deflection distribution in the real beam.
To better understand, please see the example below
Algorithm
Procedure for solving a problem
• determine the bending moment diagram in the real beam (assuming positive moments on the bottom of the beam),
• determine the equivalent/fictitious beam (according to the table below),
• load the equivalent/fictitious beam with the bending moment diagram from the real beam divided by its bending stiffness EI.

• determine the shear force and/or bending moment at the selected point in the equivalent beam, labeled as:

They will be equal to the corresponding displacements at the same point in the axis of the real beam.
-> The shear force at point K in the equivalent beam corresponds to the rotation angle at point K in the real beam,
\(\varphi(x)=Q_f (x) \)
-> The bending moment at point K in the equivalent beam corresponds to the deflection of the real beam at that point.
\( w(x)=M_f (x)\)
In the adopted reference system, displacement w>0 is directed downward, and a positive rotation angle \(\varphi>0\) is consistent with clockwise rotation.

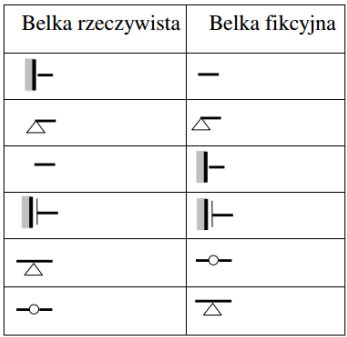
Example - Mohr's Method - transformation of supports from primary beam to secondary
Solution

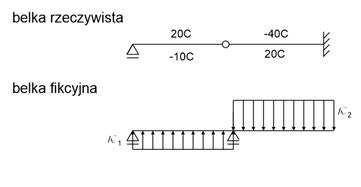
Example - Mohr's Method - effect of temperature
Solution
Of course, Mohr's Method can also be used to calculate deflections caused by temperature. We use the formula:\(\kappa=\frac{\alpha \Delta T}{h}\)
Then, the load on the fictitious beam has the value of κ and is directed towards the warmer fibers.
